Como criar uma matriz de correlação no spss
Uma matriz de correlação é uma tabela quadrada que mostra os coeficientes de correlação de Pearson entre diferentes variáveis em um conjunto de dados.
Recorde-se que o coeficiente de correlação de Pearson é uma medida da associação linear entre duas variáveis . Assume um valor entre -1 e 1 onde:
- -1 indica uma correlação linear perfeitamente negativa entre duas variáveis
- 0 indica nenhuma correlação linear entre duas variáveis
- 1 indica uma correlação linear perfeitamente positiva entre duas variáveis
Quanto mais longe o coeficiente de correlação estiver de zero, mais forte será a relação entre as duas variáveis.
Este tutorial explica como criar e interpretar uma matriz de correlação no SPSS.
Exemplo: como criar uma matriz de correlação no SPSS
Siga as etapas a seguir para criar uma matriz de correlação para este conjunto de dados que exibe a média de assistências, rebotes e pontos de oito jogadores de basquete:
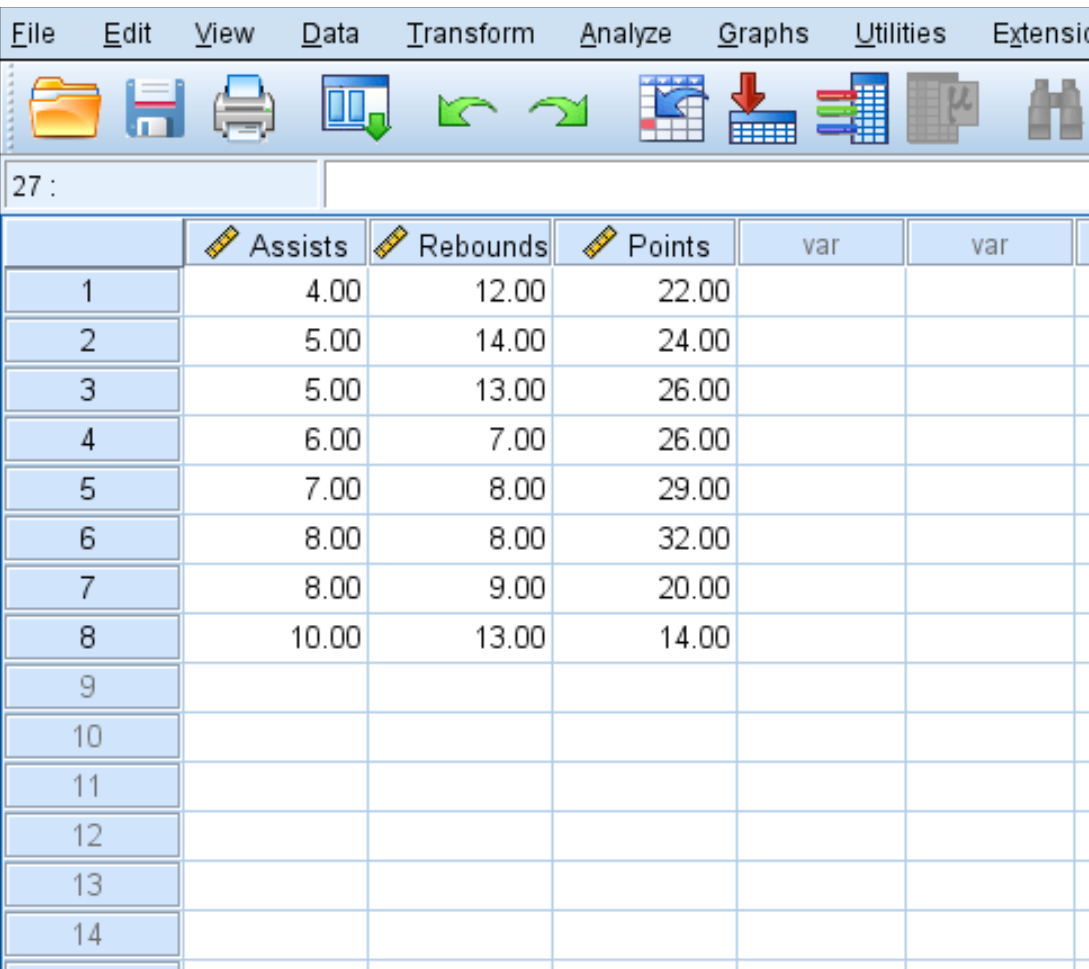
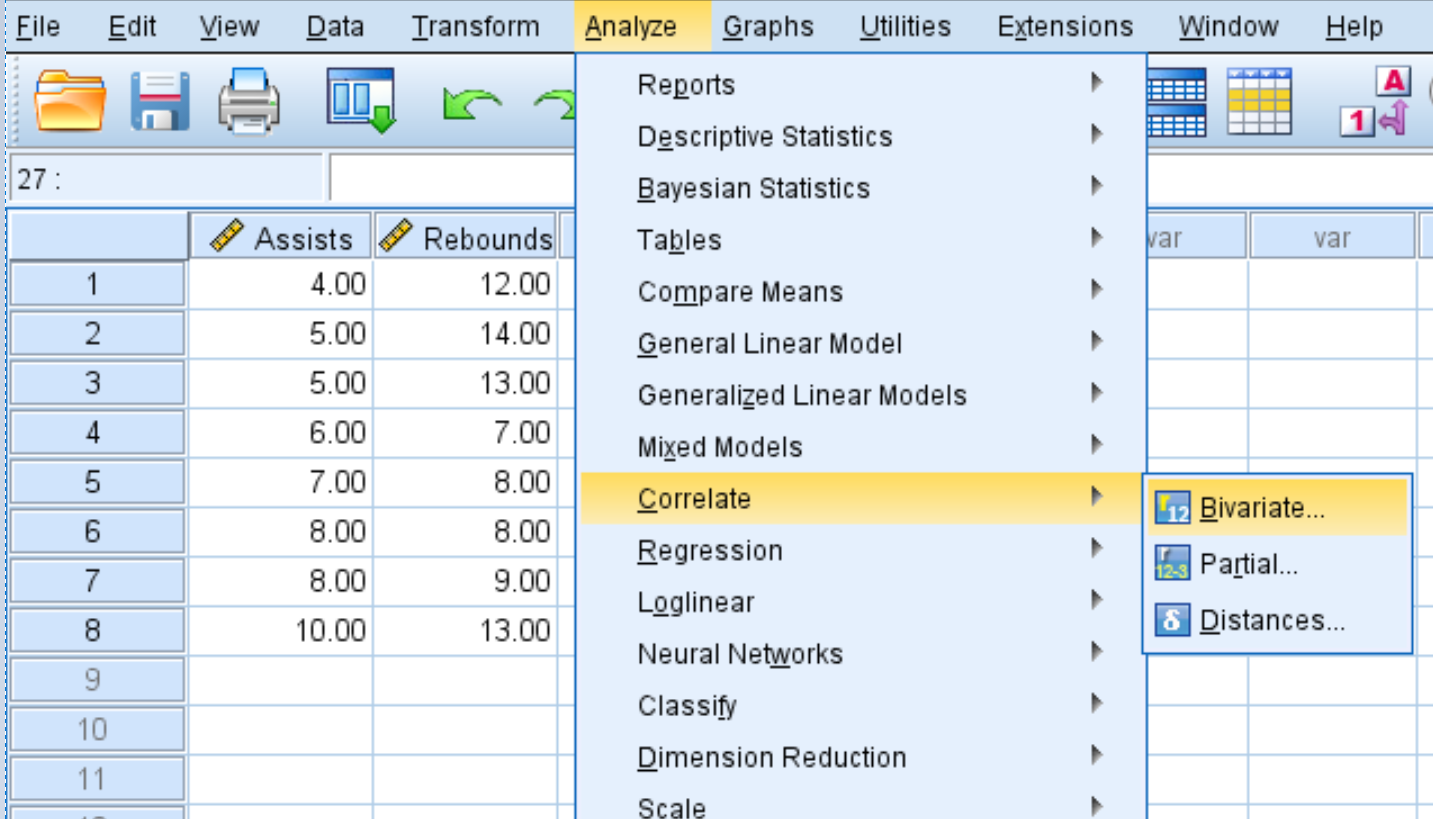
Etapa 1: Selecione Correlação Bivariada.
- Clique na guia Analisar .
- Clique em Correlacionar .
- Clique em Bivariado .
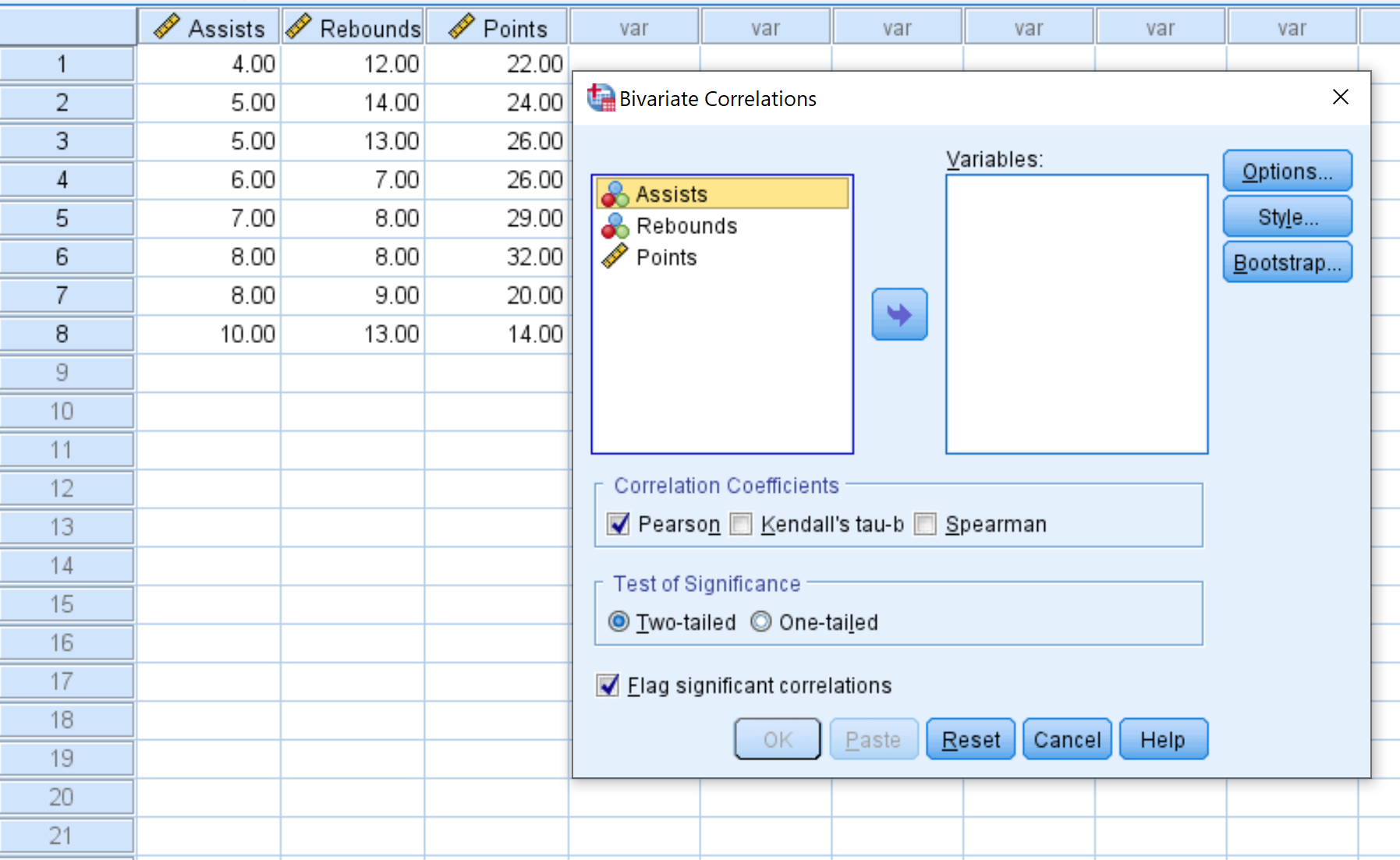
Etapa 2: Crie a matriz de correlação.
Cada variável no conjunto de dados será inicialmente exibida na caixa à esquerda:
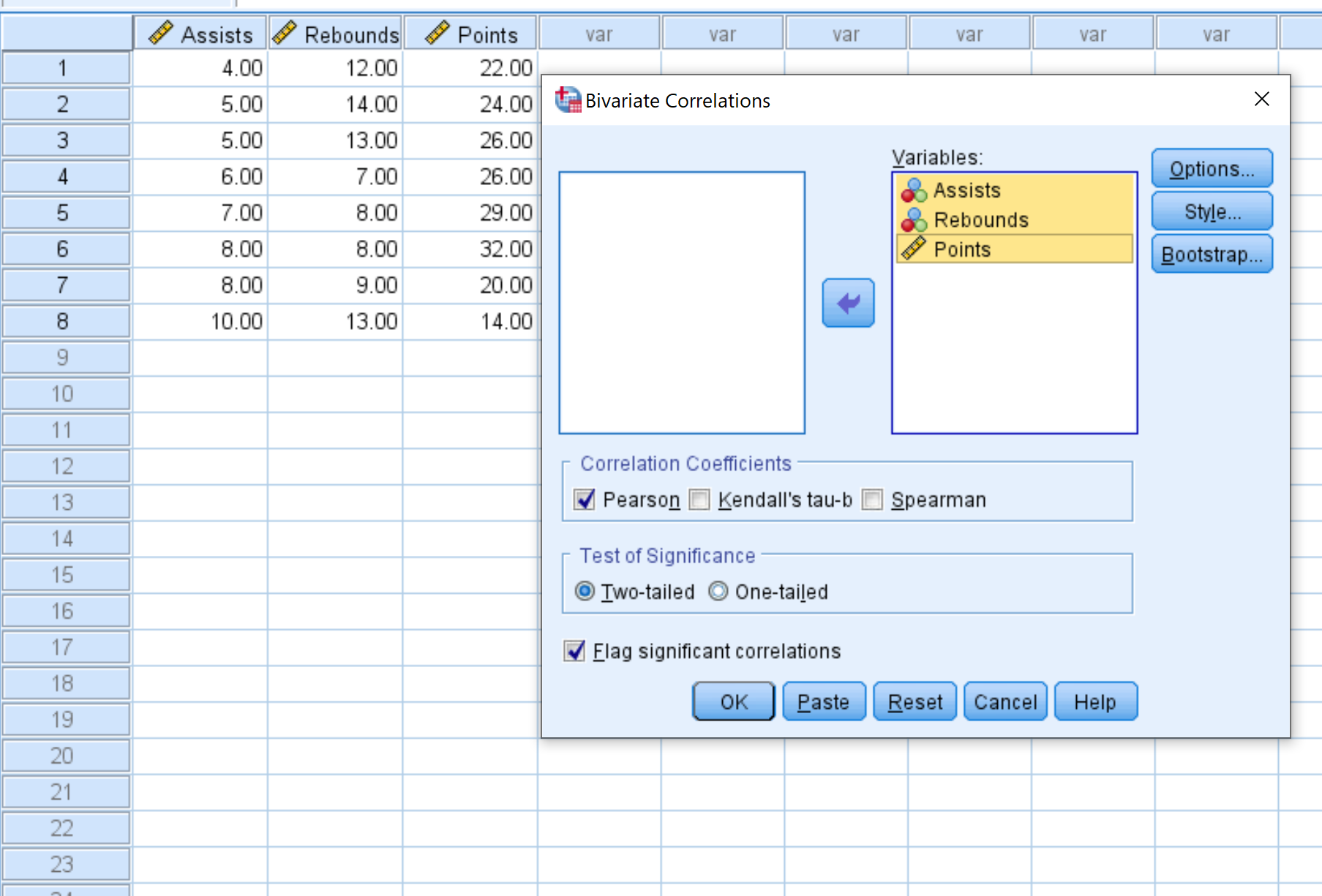
- Selecione cada variável que deseja incluir na matriz de correlação e clique na seta para transferi-las para a caixa Variáveis . Usaremos todas as três variáveis neste exemplo.
- Em Coeficientes de Correlação , escolha se deseja usar a correlação de Pearson, o tau de Kendall ou a correlação de Spearman. Deixaremos como Pearson neste exemplo.
- Em Teste de significância , escolha se deseja usar um teste bicaudal ou unilateral para determinar se duas variáveis têm uma associação estatisticamente significativa. Vamos deixar isso como bicaudal.
- Marque a caixa ao lado de Relatar correlações significativas se desejar que o SPSS relate variáveis que estão significativamente correlacionadas.
- Por fim, clique em OK .
Depois de clicar em OK , a seguinte matriz de correlação será exibida:
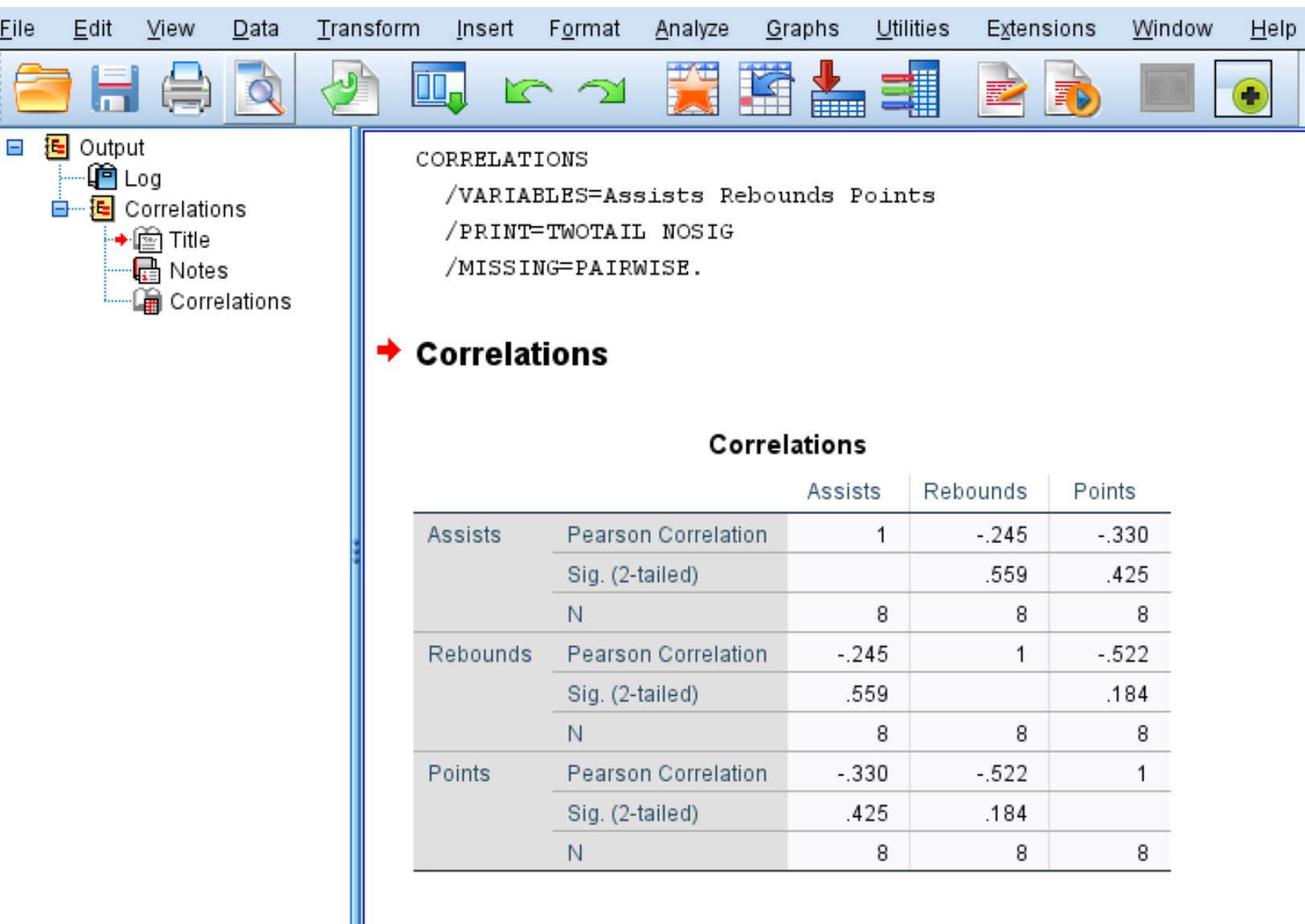
Etapa 3: Interprete a matriz de correlação.
A matriz de correlação exibe as três medidas a seguir para cada variável:
- Correlação de Pearson: medida de associação linear entre duas variáveis, variando de -1 a 1.
- Assinatura. (bicaudal): valor p bicaudal associado ao coeficiente de correlação. Isso informa se duas variáveis têm uma associação estatisticamente significativa (por exemplo, se p <0,05)
- N: número de pares utilizados para cálculo do coeficiente de correlação de Pearson.
Por exemplo, aqui está como interpretar o resultado da variável Assists:
- O coeficiente de correlação de Pearson entre assistências e rebotes é de -0,245 . Como esse número é negativo, significa que essas duas variáveis possuem uma associação negativa.
- O valor p associado ao coeficiente de correlação de Pearson para assistências e rebotes é 0,559 . Como este valor não é inferior a 0,05, as duas variáveis não apresentam associação estatisticamente significativa.
- O número de pares utilizado para calcular o coeficiente de correlação de Pearson foi 8 (por exemplo, foram utilizados 8 pares de jogadores neste cálculo).
Etapa 4: visualize a matriz de correlação.
Você também pode criar uma matriz de gráfico de dispersão para visualizar a relação linear entre cada uma das variáveis.
- Clique na guia Gráficos .
- Clique em Construtor de gráficos .
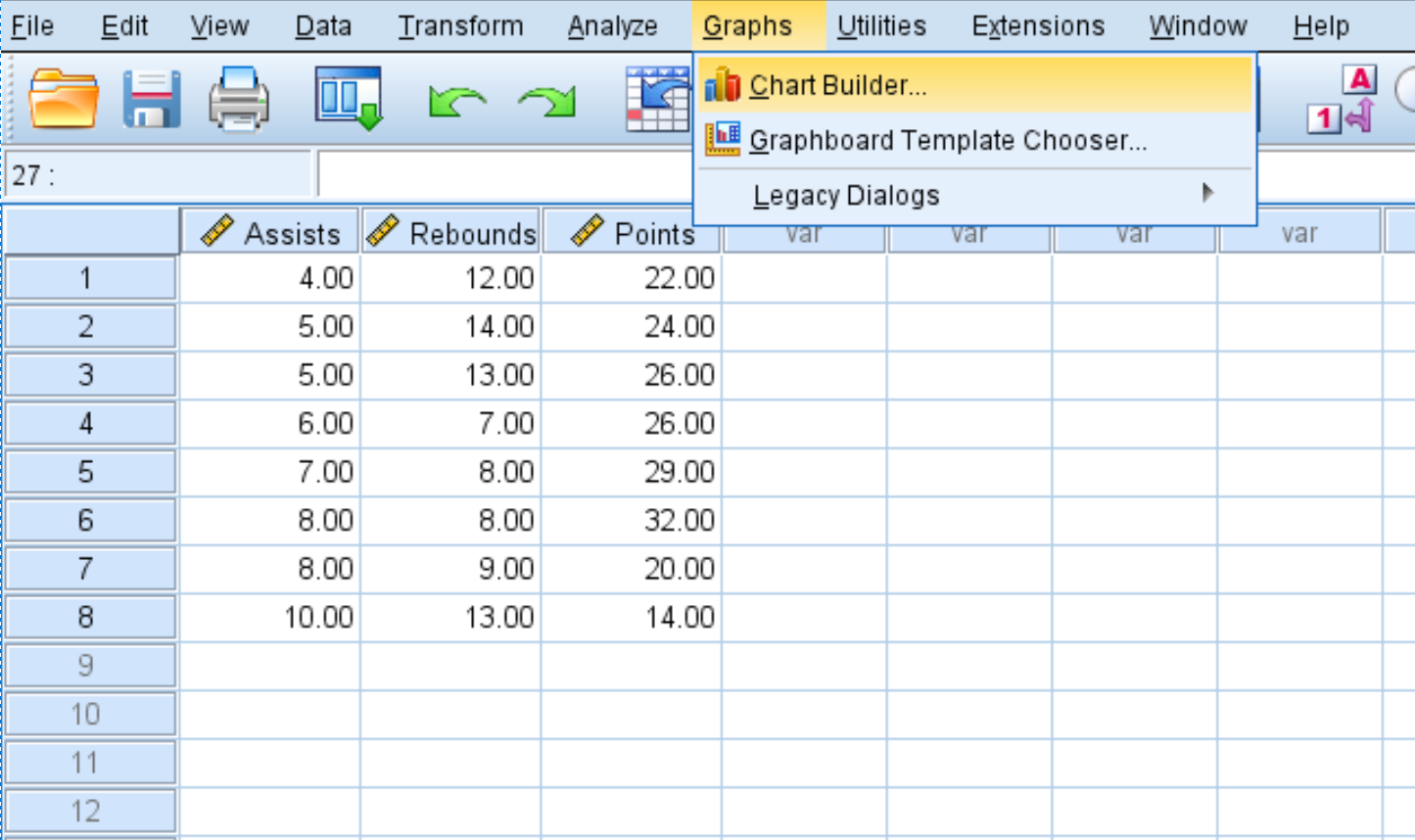
- Para tipo de gráfico, clique em Dispersão/Pontos .
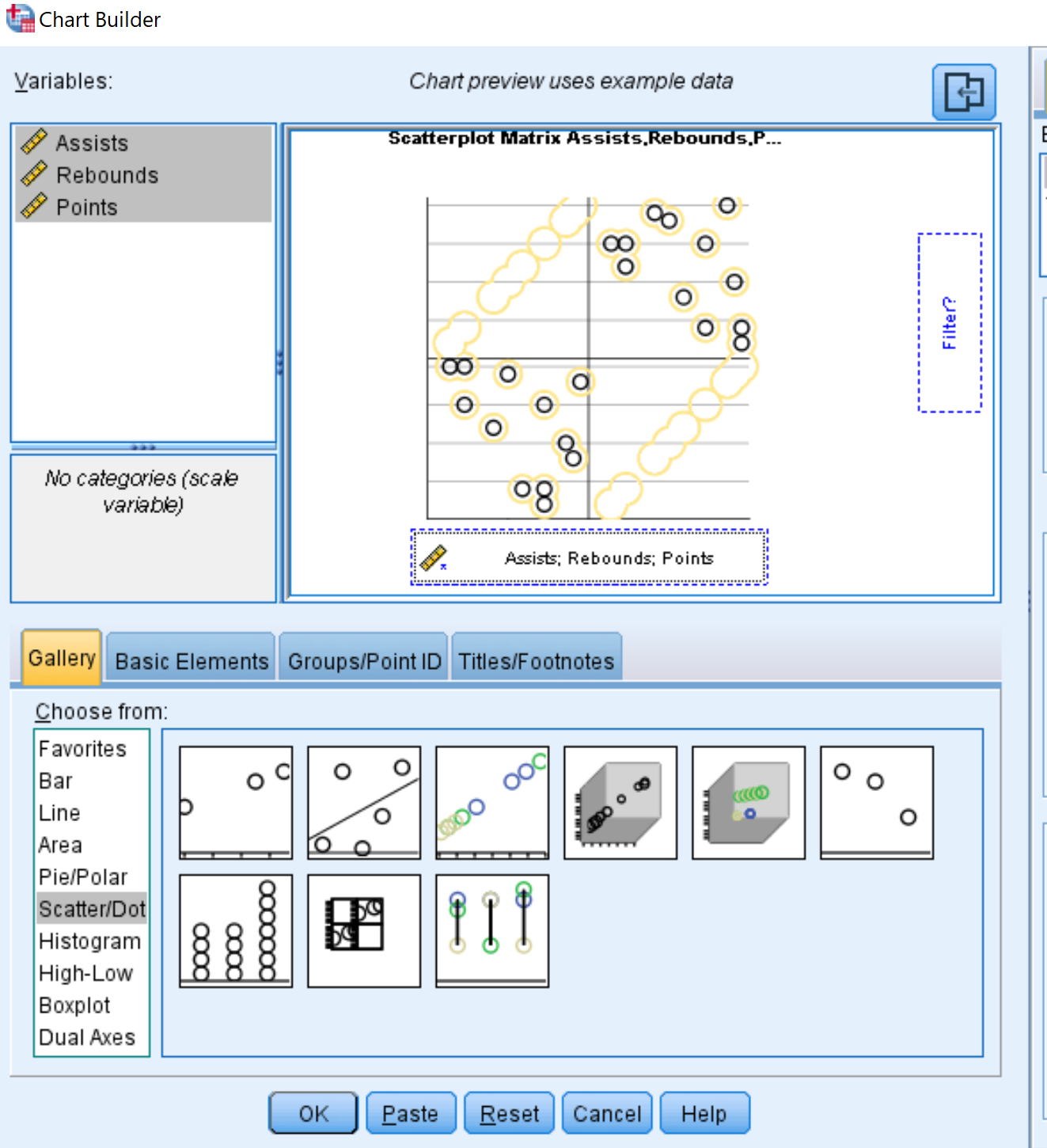
- Clique na imagem que diz Scatterplot Matrix .
- Na caixa Variáveis no canto superior esquerdo, mantenha pressionada a tecla Ctrl e clique nos três nomes de variáveis. Arraste-os para a caixa na parte inferior do gráfico que diz Scattermatrix .
- Por fim, clique em OK .
A seguinte matriz do gráfico de dispersão aparecerá automaticamente:
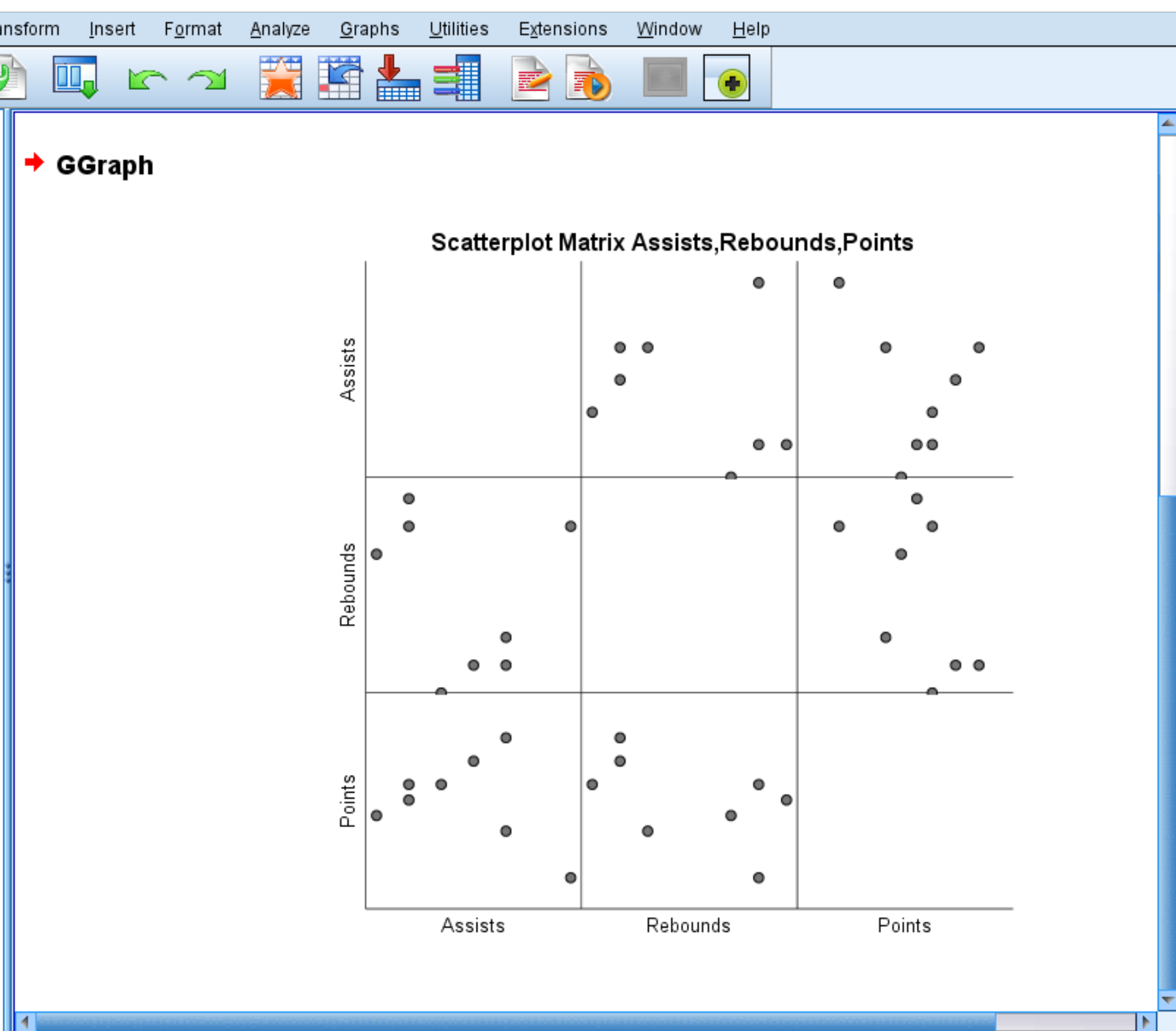
Cada gráfico de dispersão individual mostra as combinações de pares entre duas variáveis. Por exemplo, o gráfico de dispersão no canto inferior esquerdo mostra as combinações de pontos e assistências aos pares para cada um dos 8 jogadores no conjunto de dados.
Uma matriz de gráfico de dispersão é opcional, mas fornece uma boa maneira de visualizar o relacionamento entre cada combinação de variáveis em pares em um conjunto de dados.