Como realizar um teste t de uma amostra no spss
Um teste t de uma amostra é usado para testar se a média de uma população é ou não igual a um determinado valor.
Este tutorial explica como realizar um teste t de uma amostra no SPSS.
Exemplo: teste t de uma amostra no SPSS
Um botânico quer saber se a altura média de uma determinada espécie de planta é igual a 15 polegadas. Ela pega uma amostra aleatória de 12 plantas e registra a altura de cada uma em polegadas:
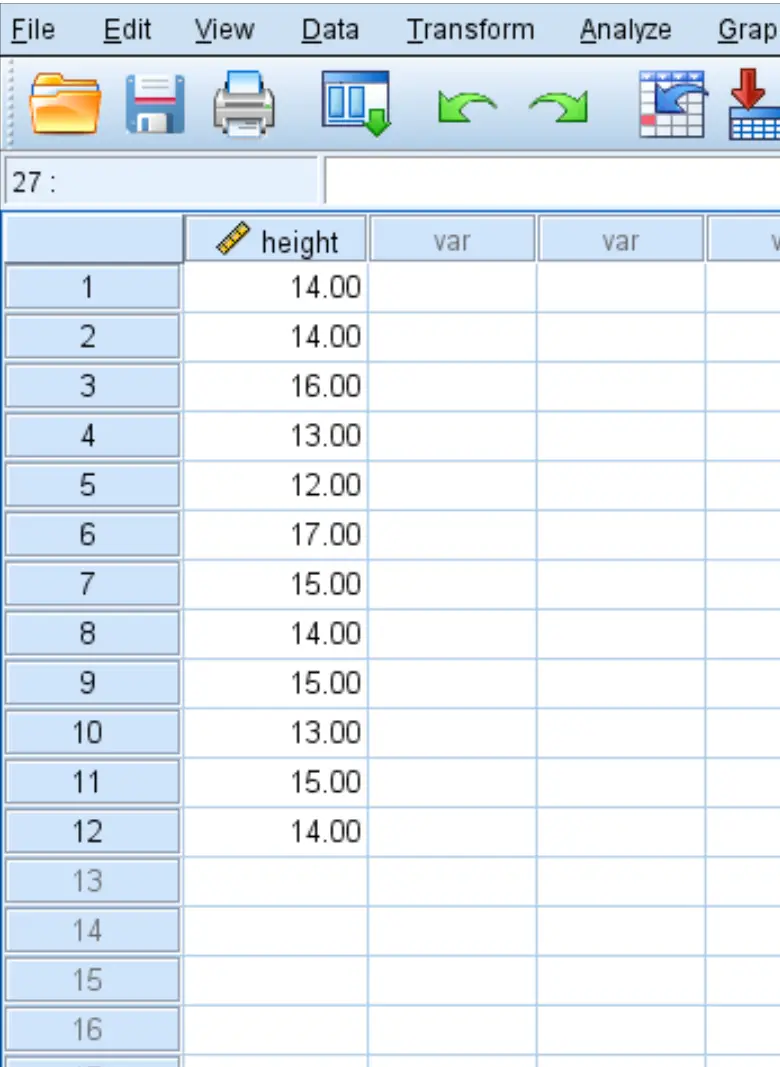
Use as etapas a seguir para realizar um teste t de uma amostra para determinar se a altura média verdadeira desta espécie de planta é igual a 15 polegadas, com base nas seguintes hipóteses nulas e alternativas:
- H 0 : μ = 15 (a média real da população é igual a 15 polegadas)
- H 1 : μ ≠ 15 (a verdadeira média da população não é igual a 15 polegadas)
Use um nível de significância de α = 0,05.
Etapa 1: Escolha a opção de teste t de uma amostra.
Clique na guia Analisar , depois em Comparar Médias e em Teste T de Uma Amostra :
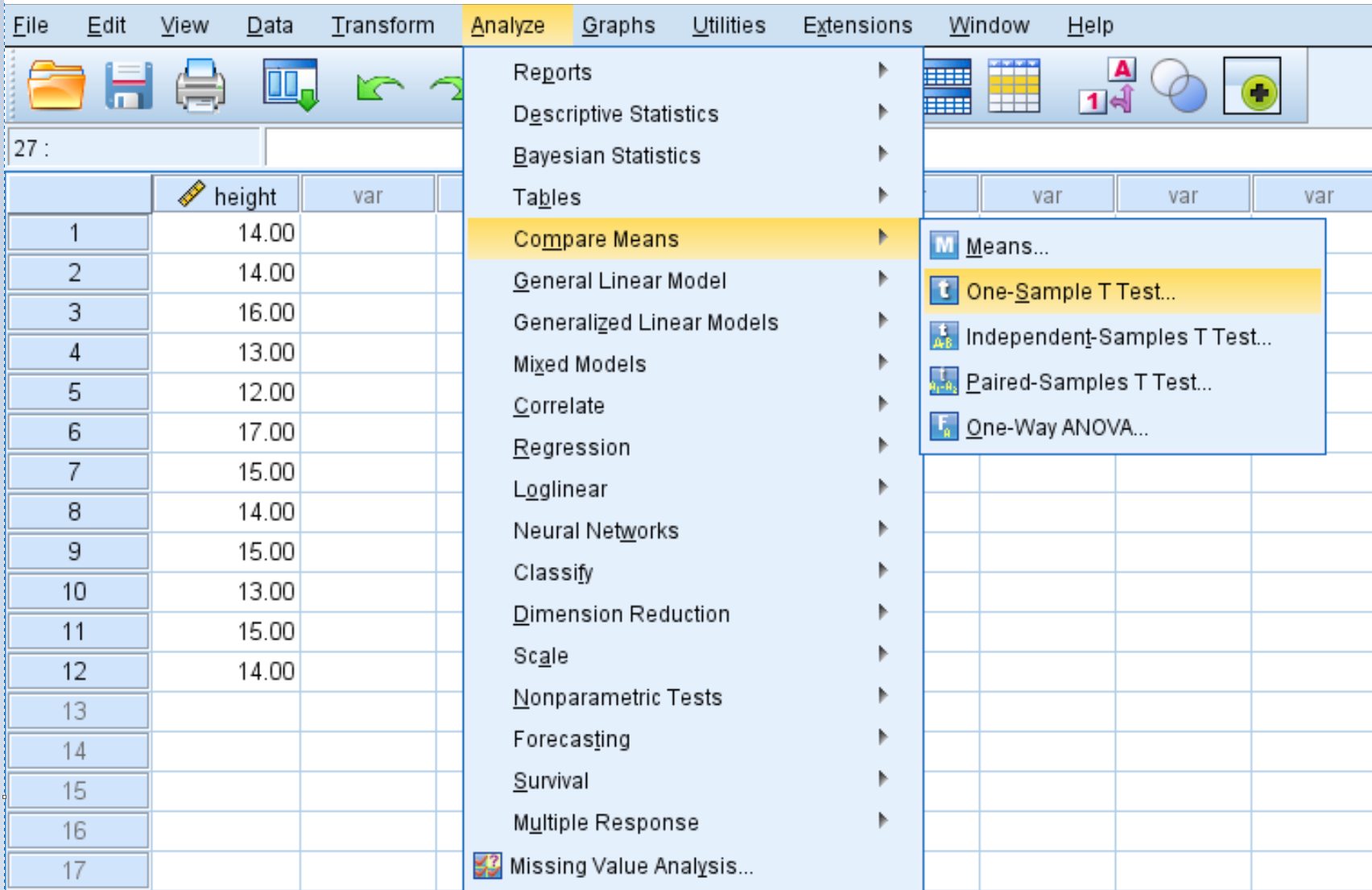
Passo 2: Preencha os valores necessários para realizar o teste t de uma amostra.
Depois de clicar em Teste T de uma amostra , a seguinte janela aparecerá:
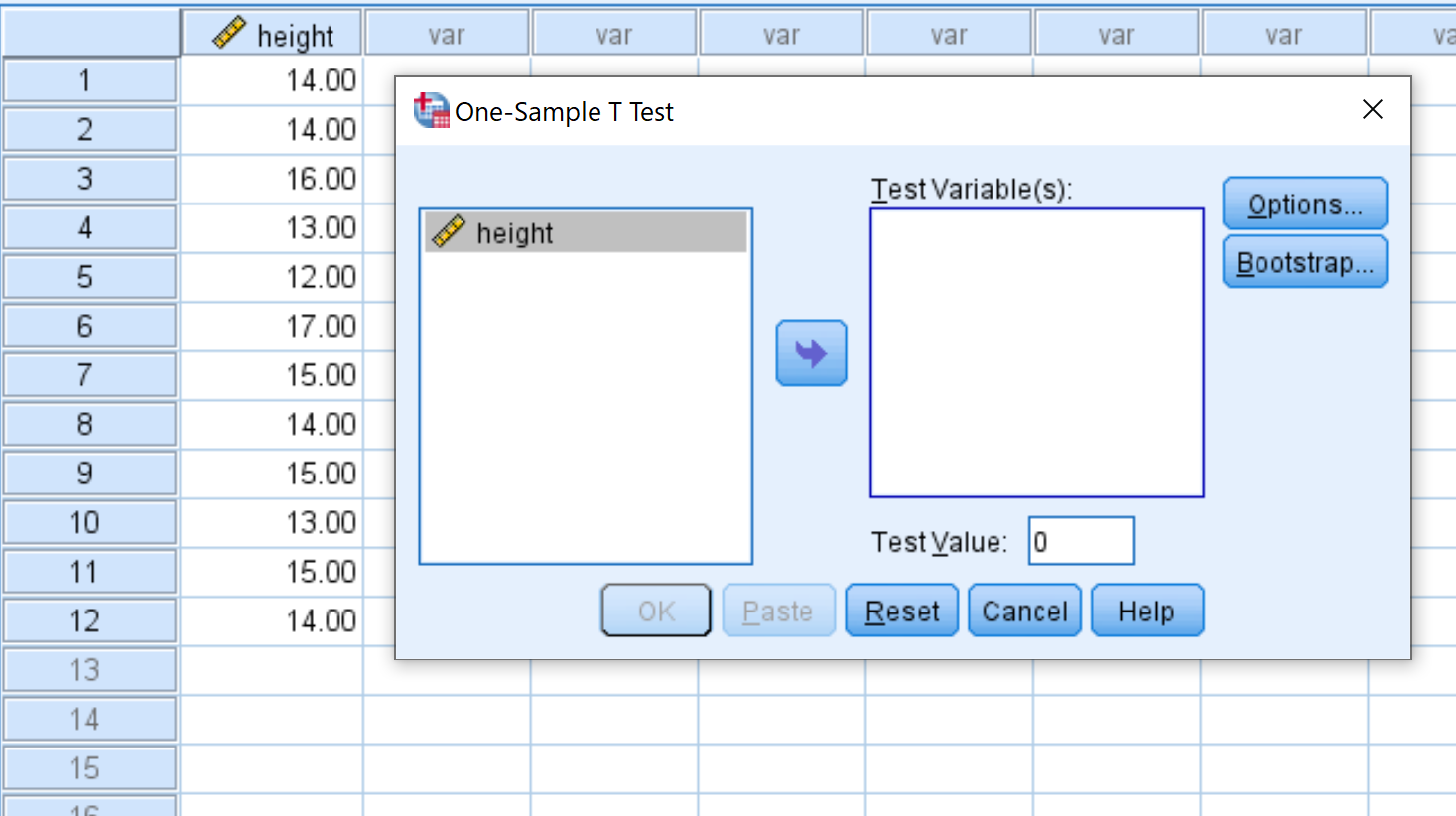
Arraste a altura da variável para a caixa denominada Test Variable(s) e altere o Test Value para 15. Em seguida, clique em OK .
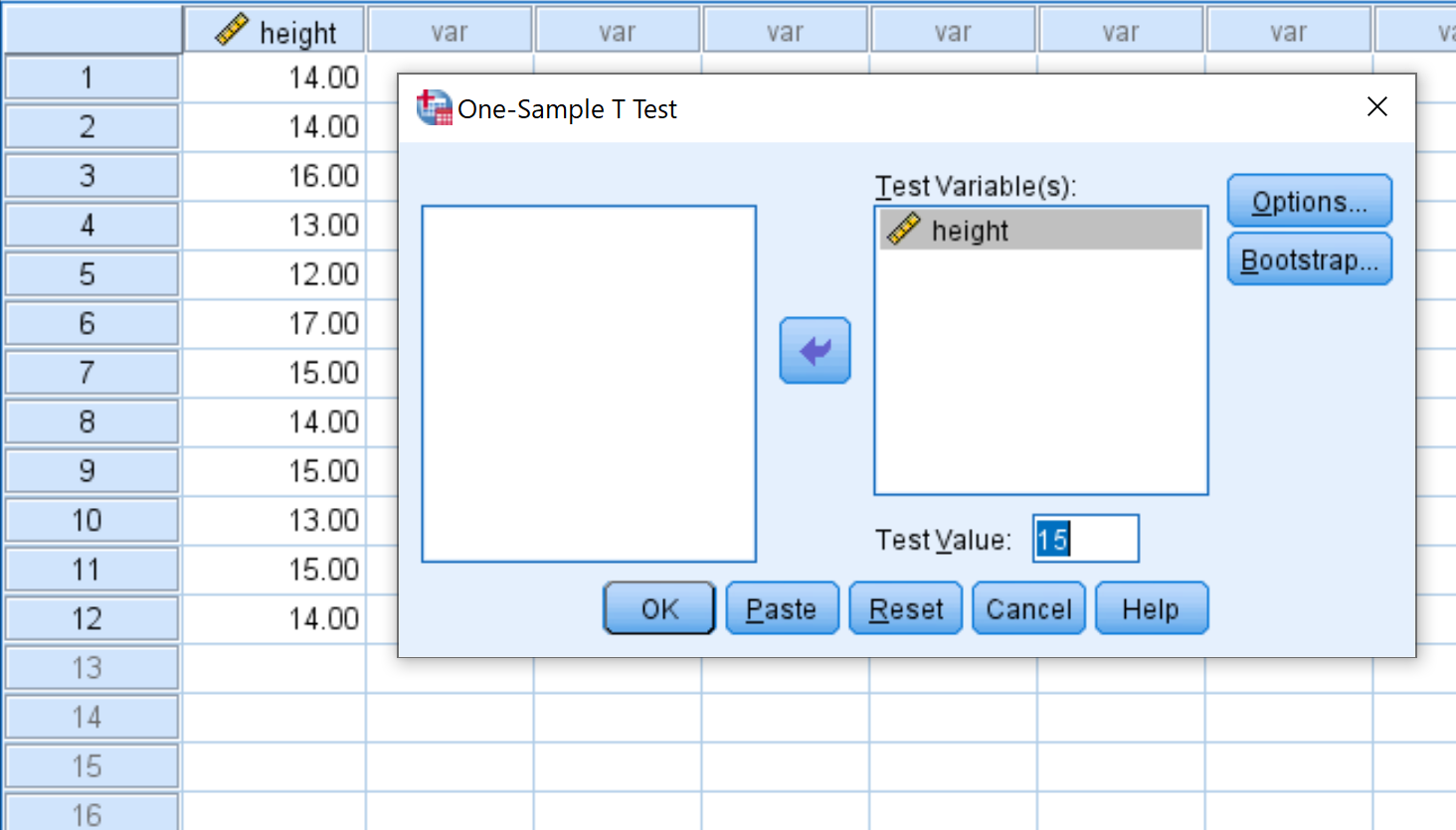
Etapa 3: interprete os resultados.
Depois de clicar em OK , os resultados do teste t de uma amostra serão exibidos:
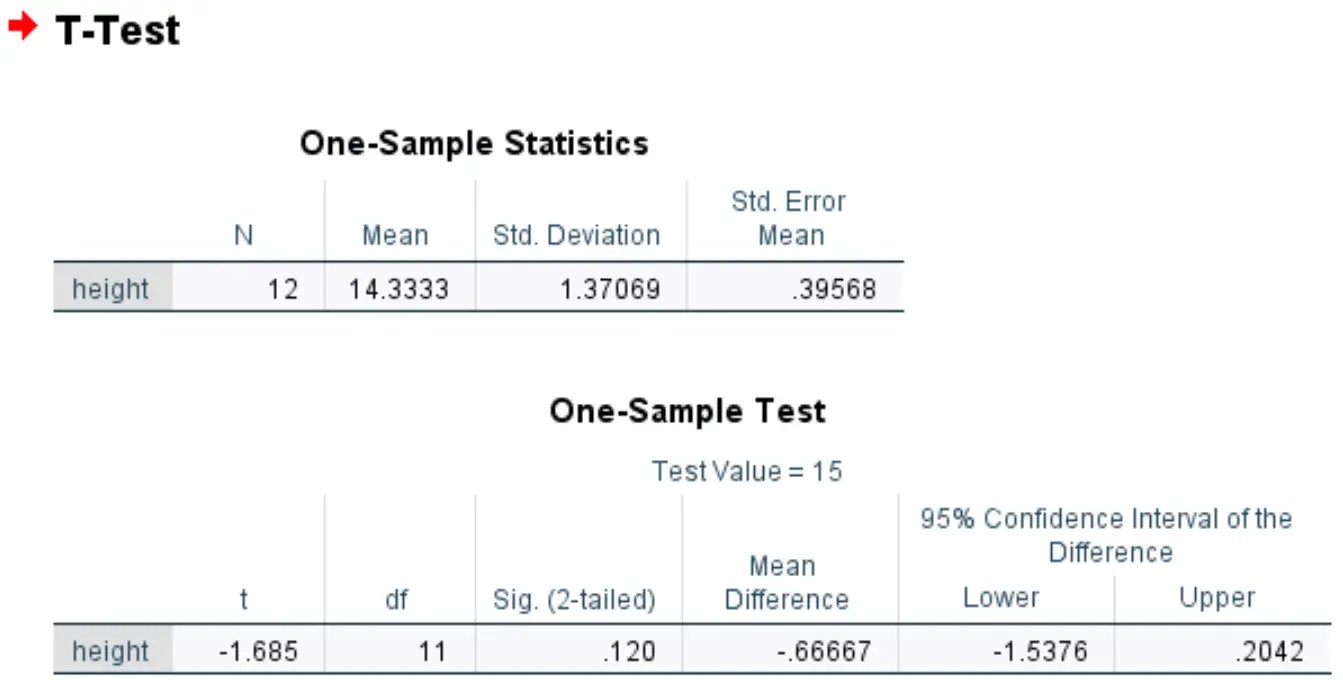
A primeira tabela exibe estatísticas resumidas para altura variável:
- N: Tamanho da amostra
- Média: a altura média das plantas na amostra
- Padrão. Desvio: O desvio padrão da altura da planta na amostra.
- Padrão. Erro médio: o erro padrão da média, calculado como s/√n
A segunda tabela exibe os resultados do teste t de uma amostra:
- t: A estatística de teste, calculada como (x – μ) / (s/√n) = (14,3333-15) / (1,37/√12) = -1,685
- df: Os graus de liberdade, calculados como n-1 = 12-1 = 11
- Assinatura. (bicaudal): O valor p bicaudal que corresponde a um valor de -1,685 com df = 11
- Diferença média: a diferença entre a média da amostra e a média hipotética
- IC 95% de diferença: intervalo de confiança de 95% para a verdadeira diferença entre a média amostral e a média hipotética.
Como o valor p do teste (0,120) não é inferior a 0,05, não rejeitamos a hipótese nula. Não temos evidências suficientes para dizer que a verdadeira altura média desta espécie de planta seja diferente de 15 polegadas.