Como realizar o teste levene no spss

O teste de Levene é usado para determinar se dois ou mais grupos têm variâncias iguais.

É amplamente utilizado porque muitos testes estatísticos baseiam-se na suposição de que os grupos têm variâncias iguais .

Este tutorial explica como realizar o teste Levene no SPSS.

Exemplo: teste Levene no SPSS

Os pesquisadores querem saber se três fertilizantes diferentes levam a diferentes níveis de crescimento das plantas.

Eles selecionam aleatoriamente 30 plantas diferentes e as dividem em três grupos de 10, aplicando um fertilizante diferente em cada grupo. Depois de um mês, medem a altura de cada planta.

A captura de tela a seguir mostra a quantidade de crescimento (em polegadas) de cada planta individual, junto com o fertilizante (1, 2 ou 3) que foi aplicado à planta:

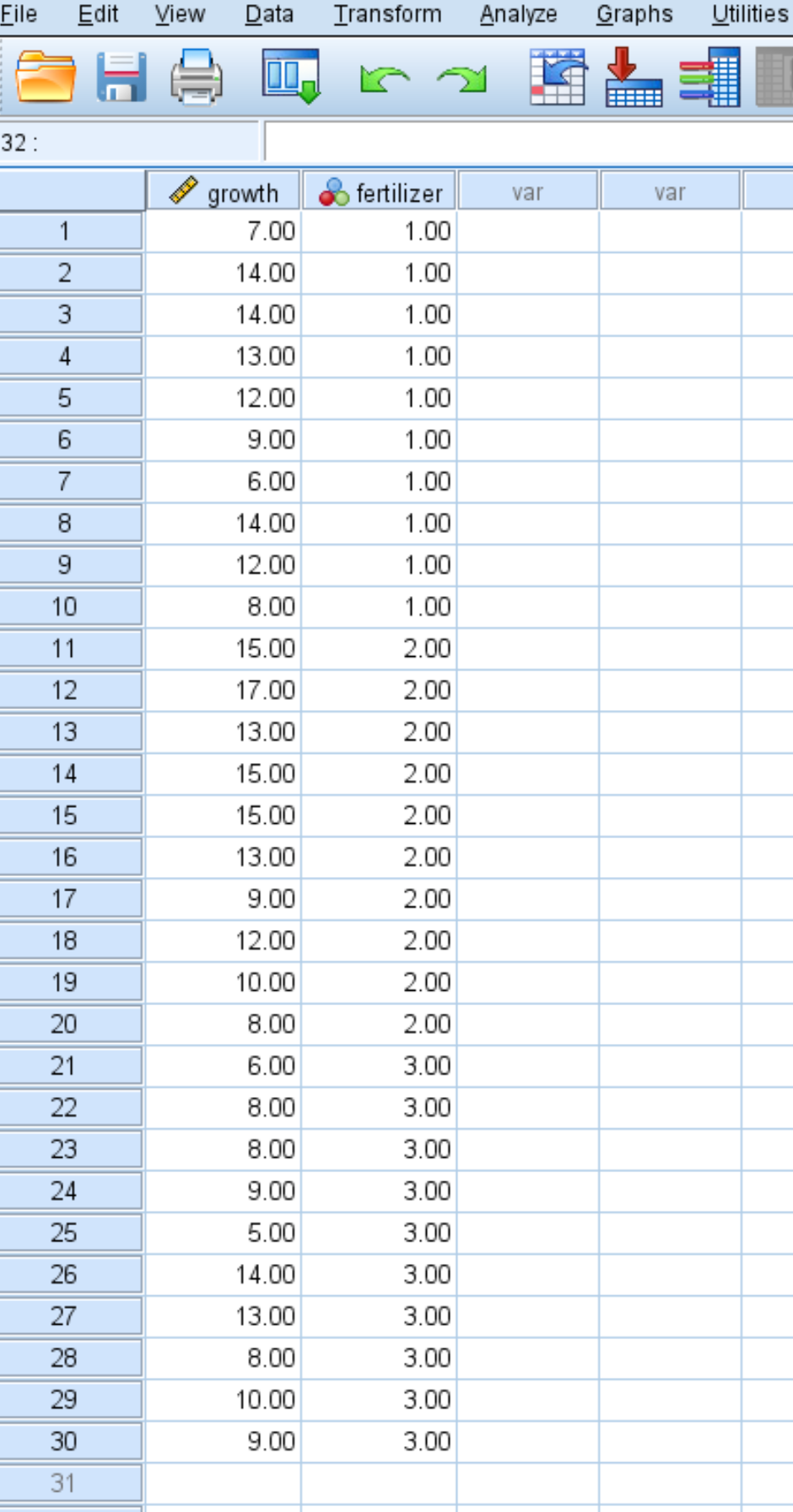
Siga as etapas a seguir para realizar o teste de Levene no SPSS para determinar se os três grupos têm ou não variâncias iguais.

Passo 1: Escolha a opção Explorar.

Clique na guia Analisar , depois em Estatísticas Descritivas e em Explorar :

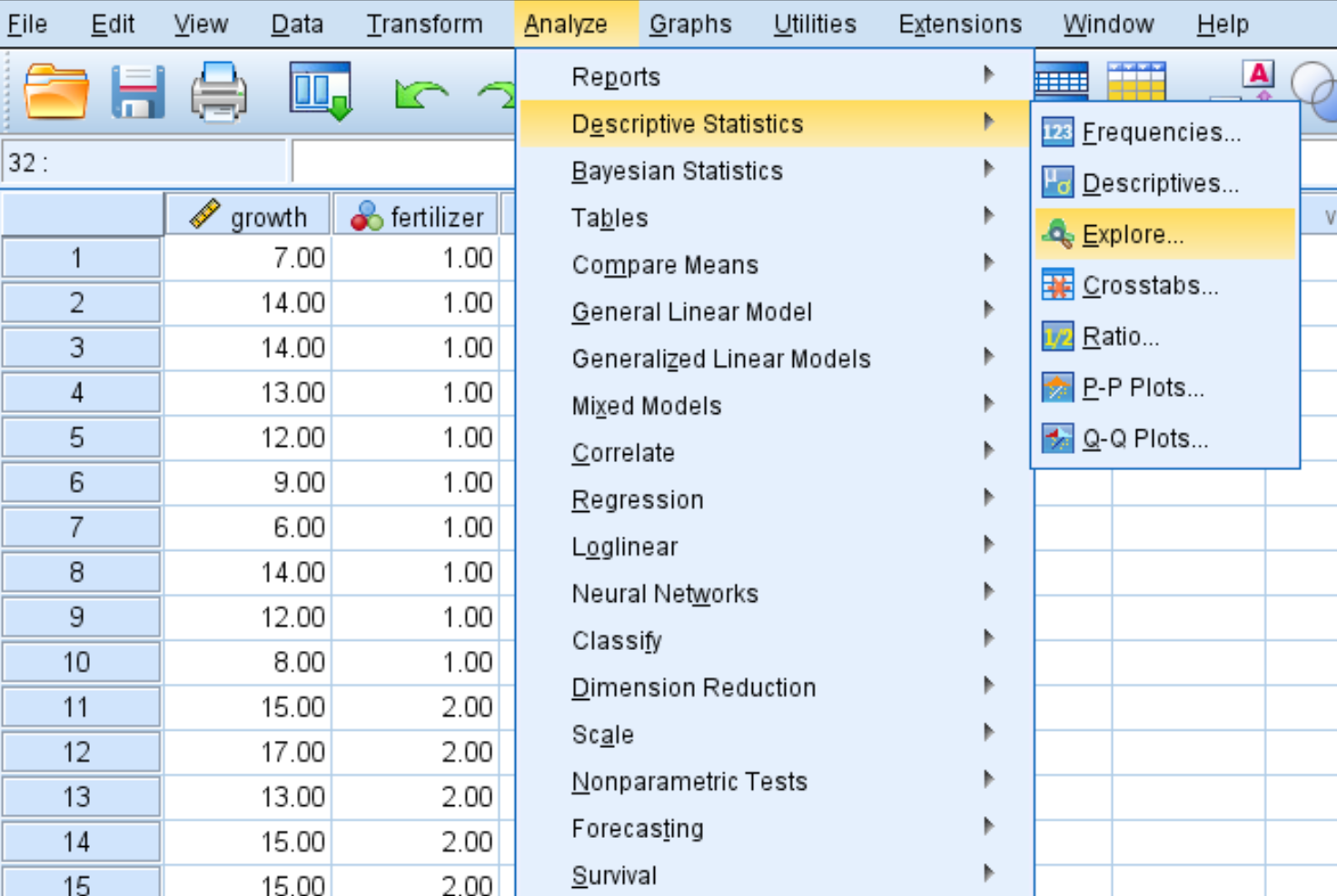
Passo 2: Preencha os valores necessários para realizar o teste.

Arraste o crescimento para a caixa em Lista de Dependentes e arraste fertilizar   na caixa em Lista de Fatores.

Em seguida, clique em Plots e certifique-se de que Estimativa de energia esteja selecionada. Em seguida, clique em continuar . Em seguida, clique em OK .

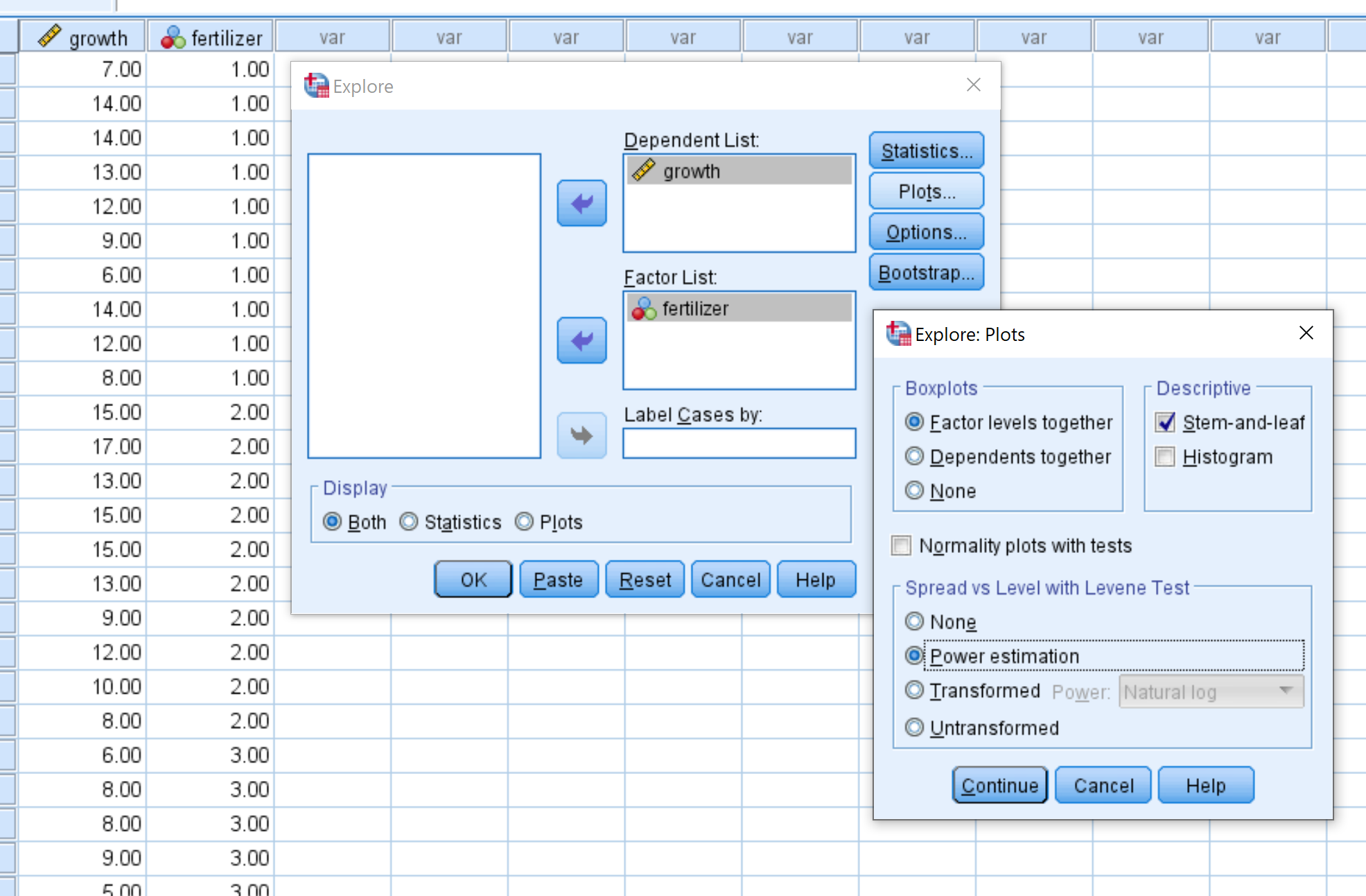
Etapa 3: interprete os resultados.

Depois de clicar em OK , os resultados do teste Levene serão exibidos:

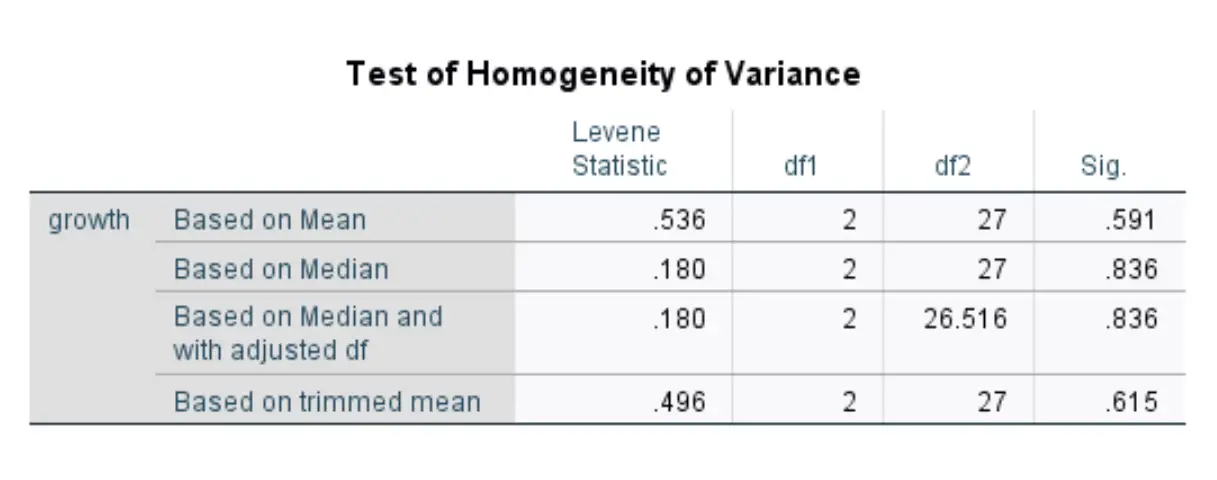
Esta tabela exibe estatísticas de teste para quatro versões diferentes do teste Levene. Os números que nos interessam estão na primeira linha, que exibe os resultados do teste de Levene com base na média.

A estatística de teste é 0,536 e o valor p correspondente é 0,591* .

Como esse valor p não é inferior a 0,05, não rejeitamos a hipótese nula.

Isto significa que não temos provas suficientes para afirmar que a variação no crescimento das plantas entre os três fertilizantes é significativamente diferente.

Em outras palavras, os três grupos têm variâncias iguais. Se realizássemos um teste estatístico (como uma ANOVA unidirecional ) que assumisse que cada grupo tem variância igual, então essa suposição seria atendida.

* Este valor p corresponde a uma estatística F de 0,536 com numerador df = 2 e denominador df = 27. Este valor p também pode ser calculado usando a calculadora de distribuição F.