Como realizar regressão linear simples no spss
A regressão linear simples é um método que podemos usar para compreender a relação entre uma variável preditora e uma variável de resposta.
Este tutorial explica como realizar uma regressão linear simples no SPSS.
Exemplo: Regressão Linear Simples em SPSS
Digamos que temos o seguinte conjunto de dados que mostra o número de horas estudadas e a nota do exame obtida por 20 alunos:
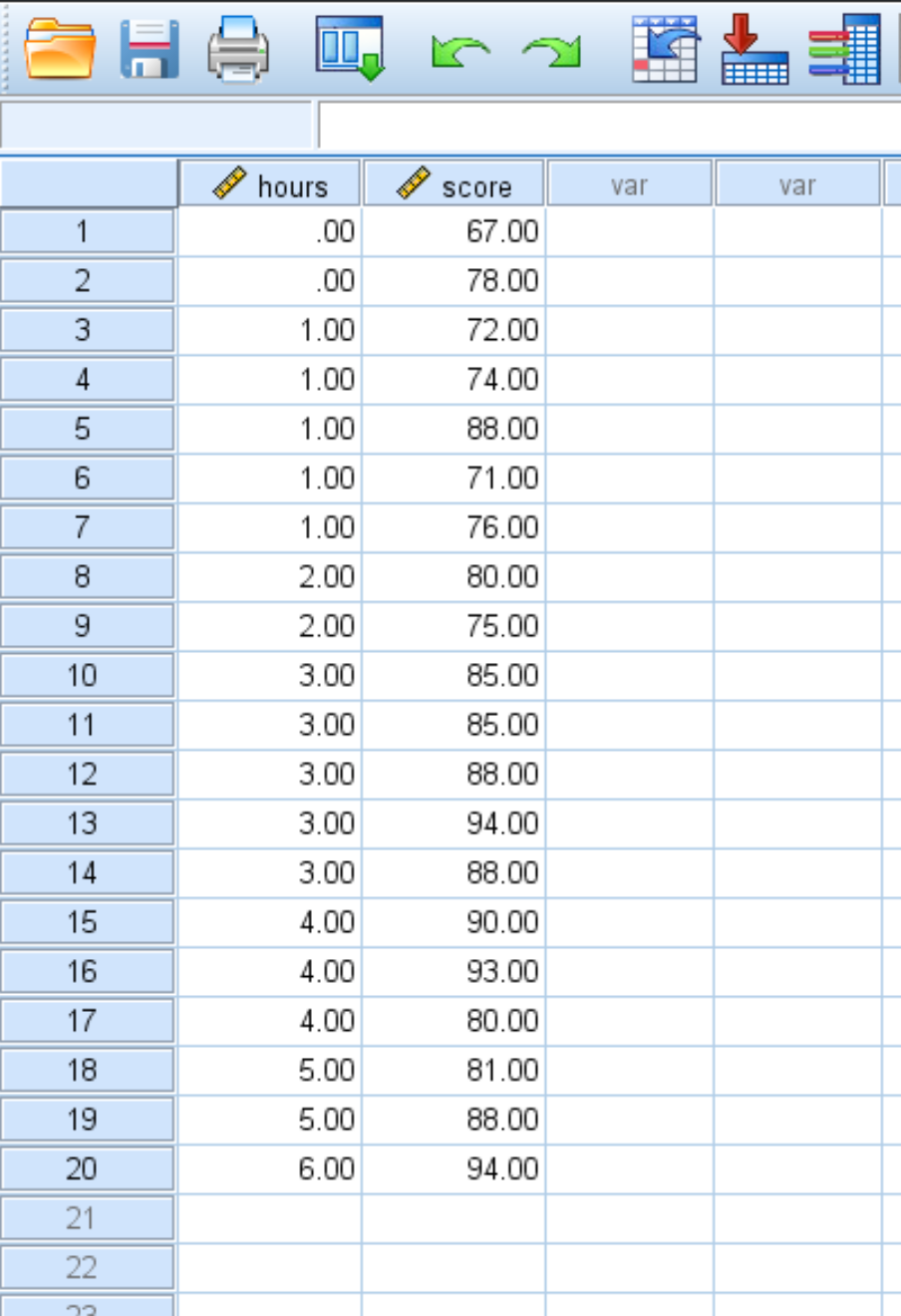
Use as etapas a seguir para realizar uma regressão linear simples neste conjunto de dados para quantificar a relação entre horas estudadas e pontuação no exame:
Etapa 1: visualize os dados.
Primeiro, criaremos um gráfico de dispersão para visualizar a relação entre horas e pontuação para garantir que a relação entre as duas variáveis pareça linear. Caso contrário, a regressão linear simples não será uma técnica apropriada a ser usada.
Clique na guia Gráficos e em Construtor de Gráficos :
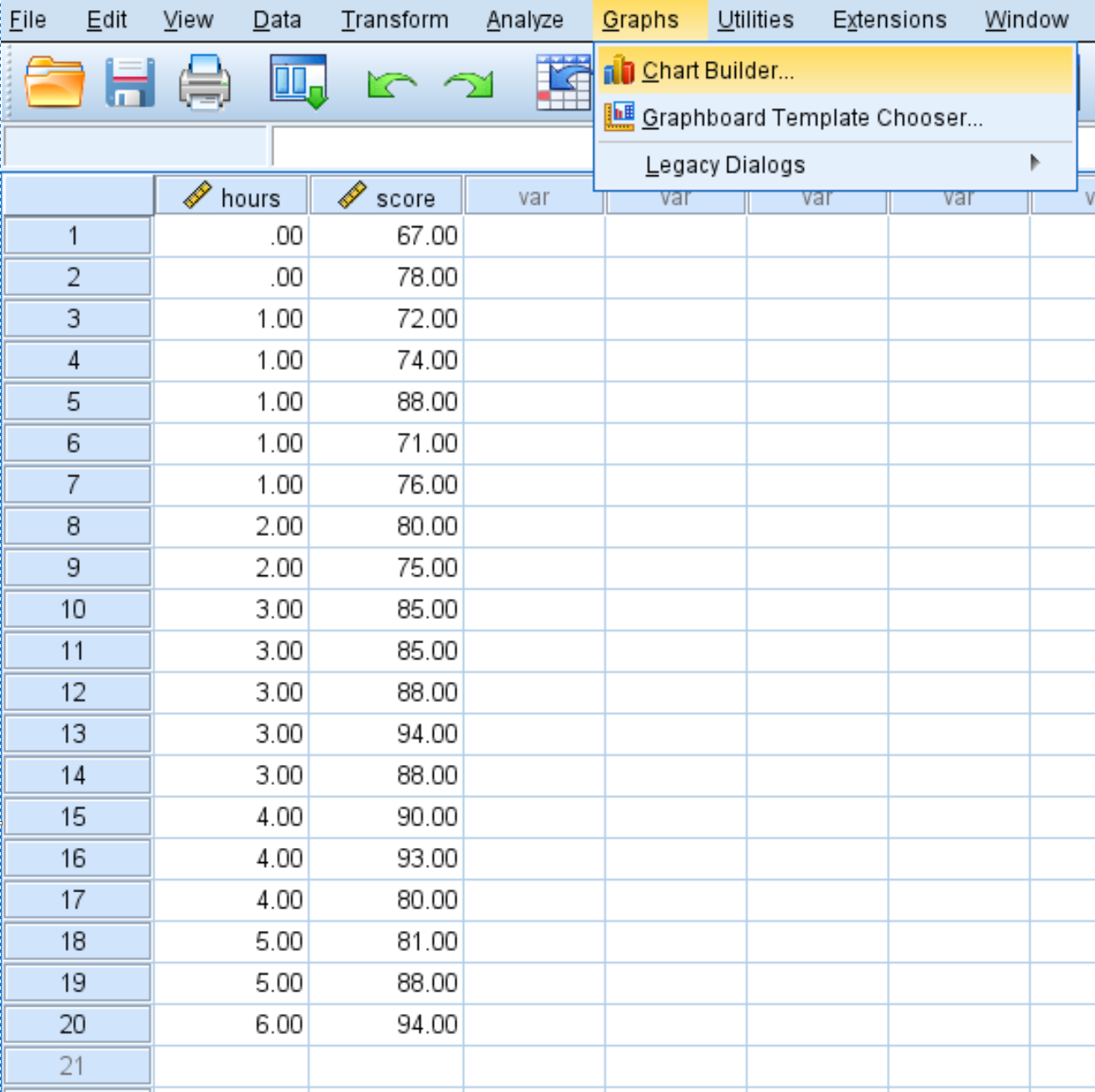
No menu Escolher de , clique e arraste Dispersão/Ponto para a janela principal de edição. Em seguida, arraste os tempos variáveis para o eixo x e a pontuação para o eixo y.
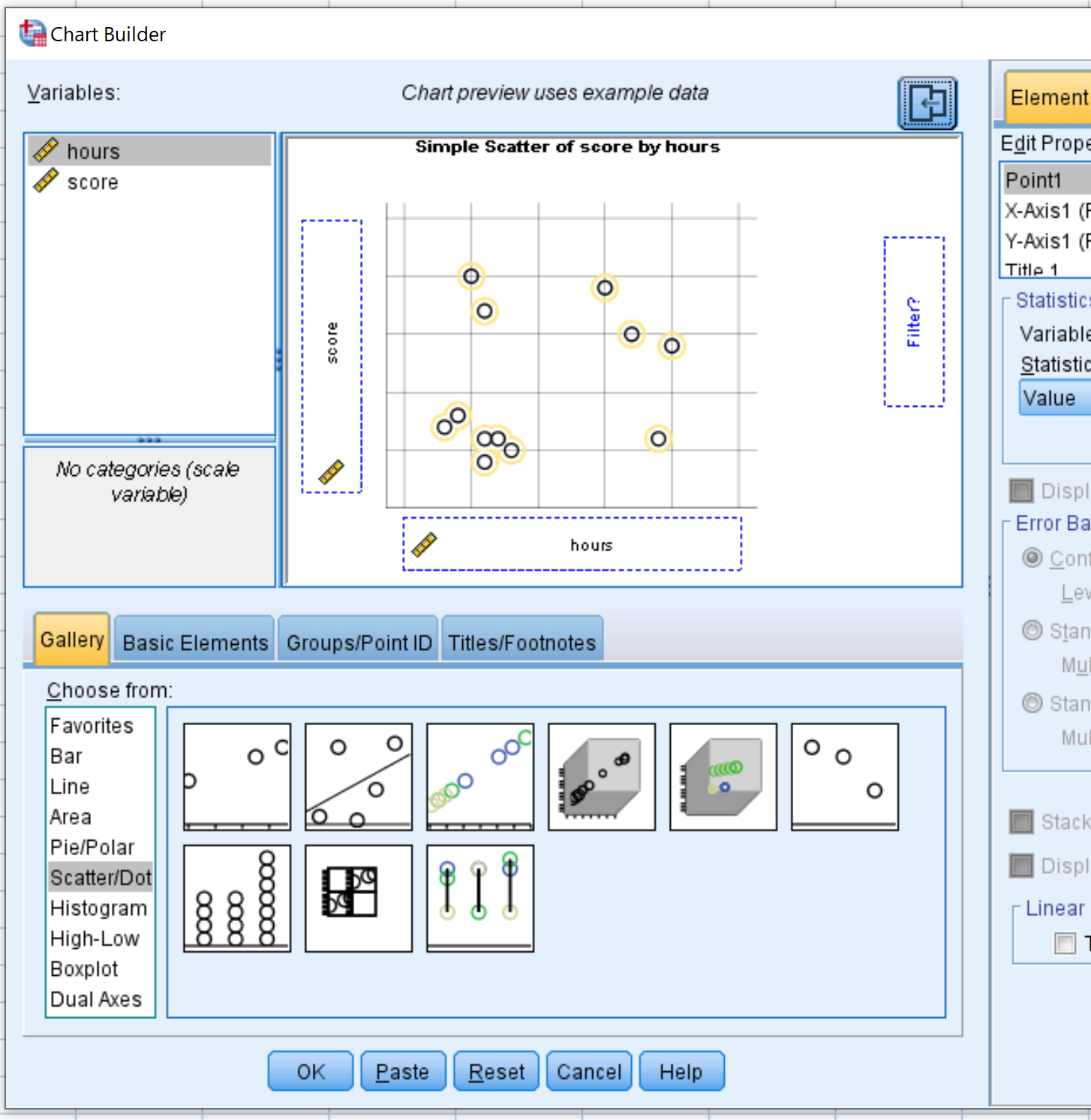
Depois de clicar em OK , o seguinte gráfico de dispersão aparecerá:
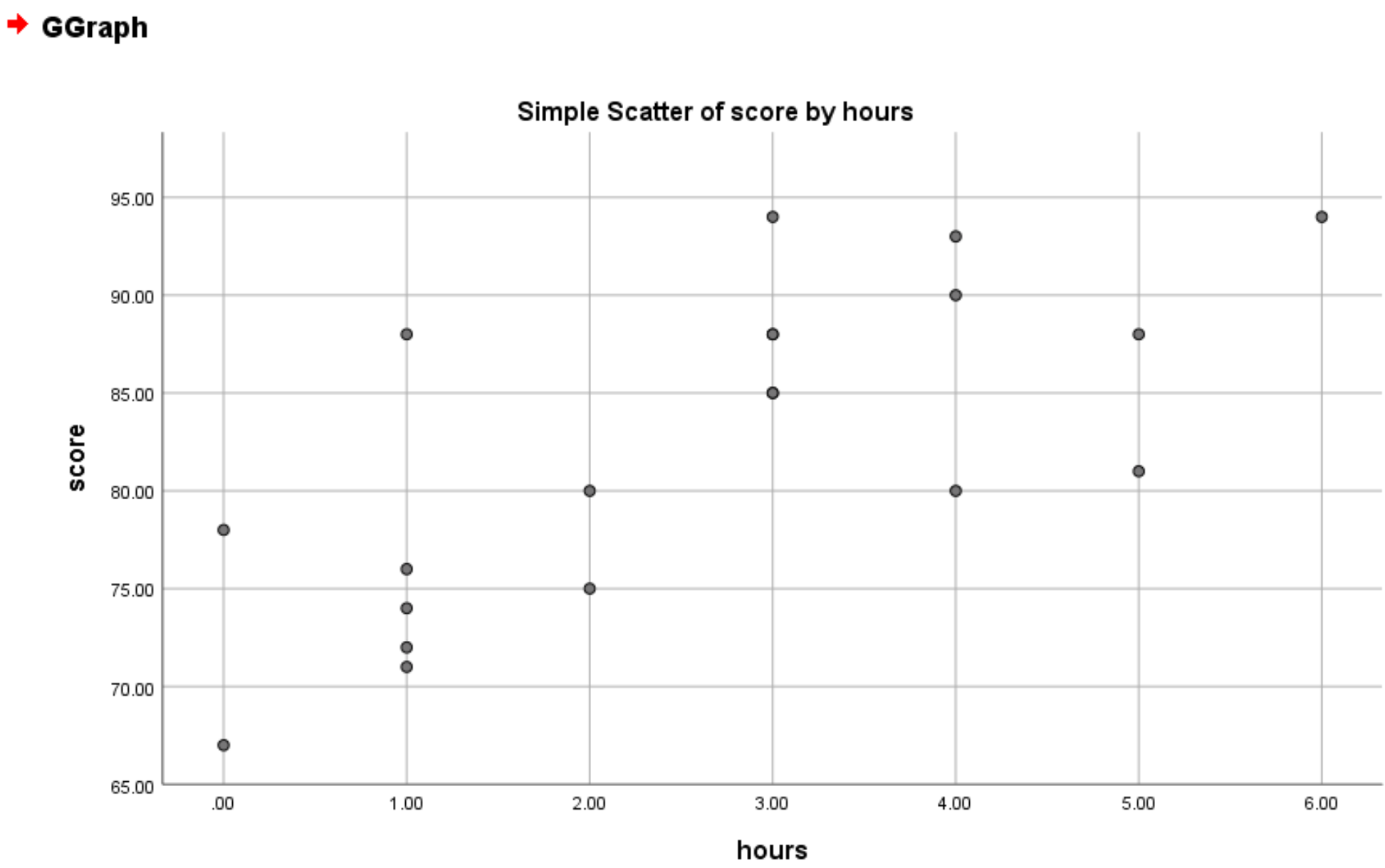
Pelo gráfico, podemos perceber que existe uma relação linear positiva entre horas e pontuação. Em geral, os alunos que estudam mais horas tendem a ter pontuações mais altas.
Como existe uma relação linear clara entre as duas variáveis, procederemos ao ajuste de um modelo de regressão linear simples ao conjunto de dados.
Etapa 2: ajuste um modelo de regressão linear simples.
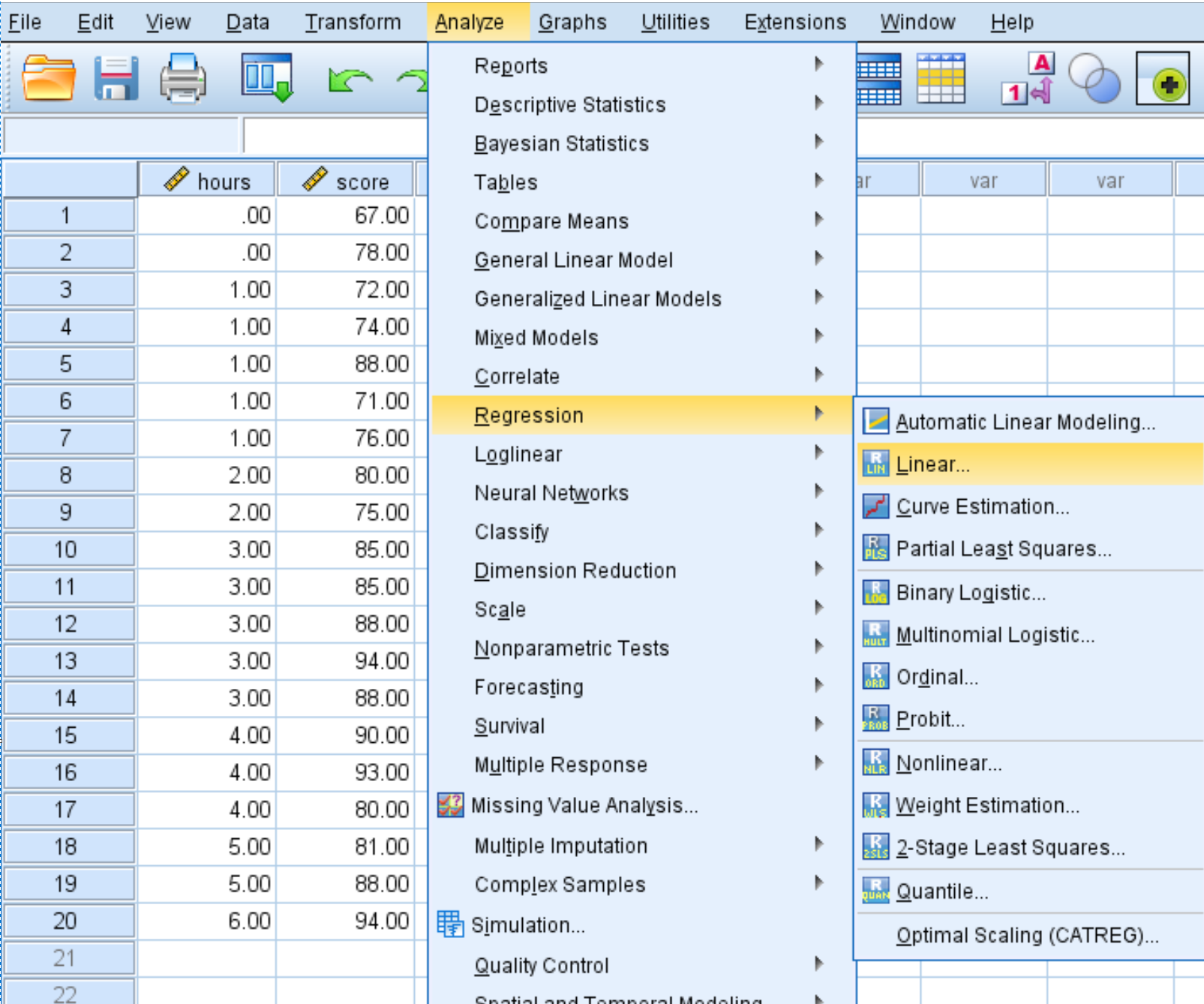
Clique na guia Analisar , depois em Regressão e depois em Linear :
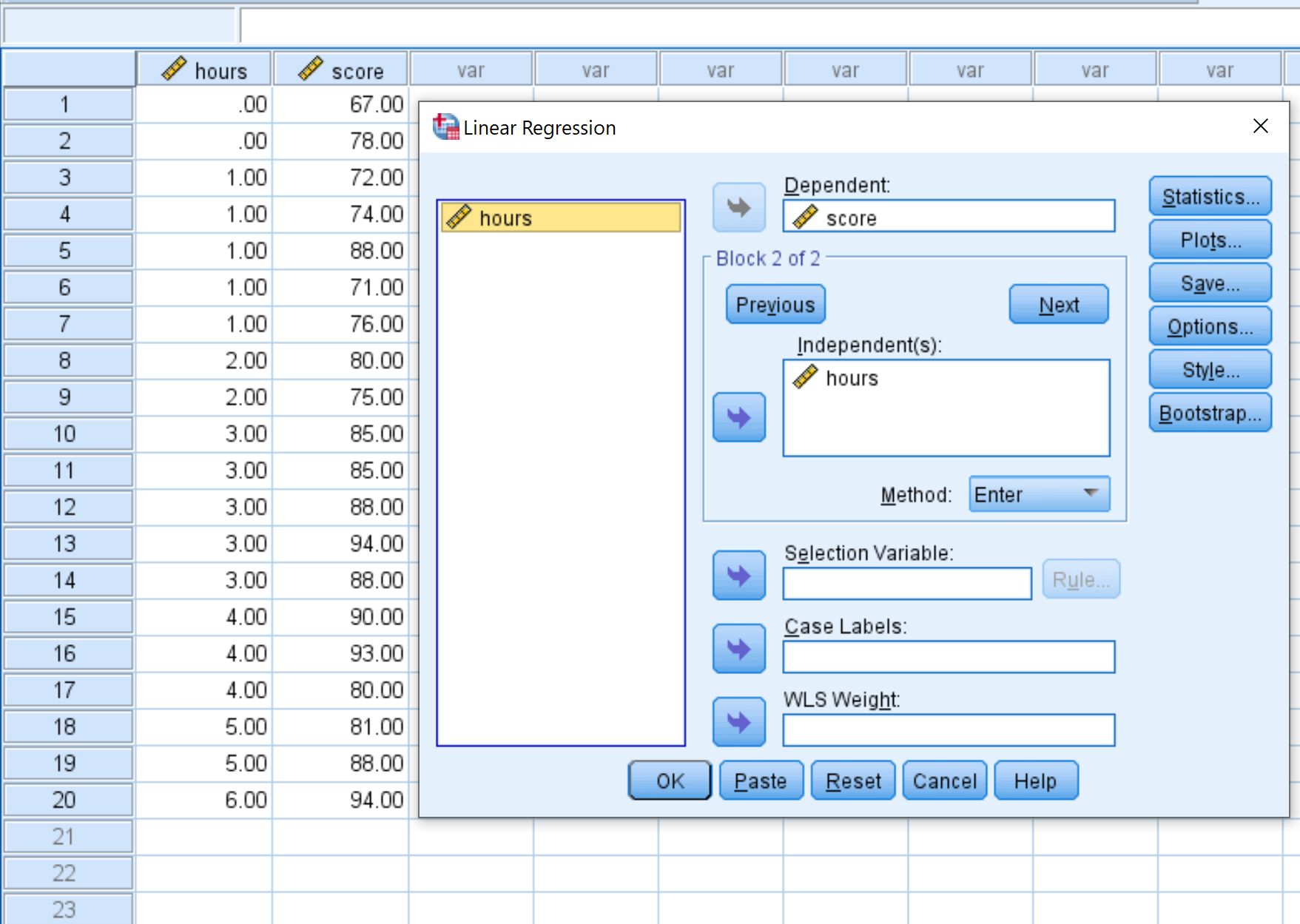
Na nova janela que aparece, arraste a pontuação da variável para a caixa denominada Dependente e arraste as horas para a caixa denominada Independente. Em seguida, clique em OK .
Etapa 3: interprete os resultados.
Depois de clicar em OK , os resultados da regressão linear simples aparecerão. A primeira tabela que nos interessa é a intitulada Resumo do Modelo :
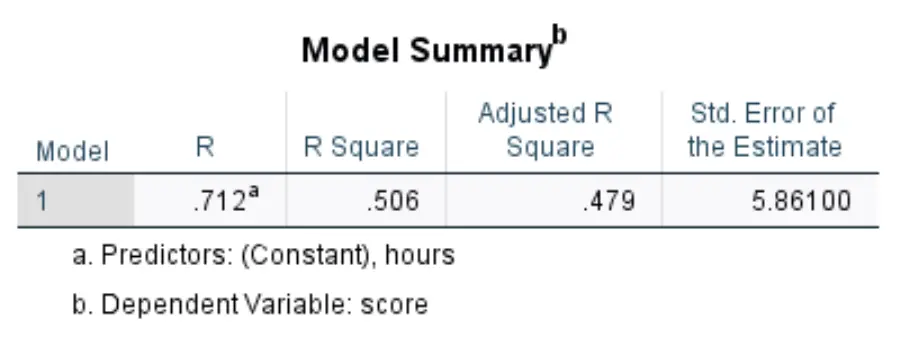
Veja como interpretar os números mais relevantes nesta tabela:
- R Quadrado: Esta é a proporção da variância na variável resposta que pode ser explicada pela variável explicativa. Neste exemplo, 50,6% da variação nas notas dos exames pode ser explicada pelas horas estudadas.
- Padrão. Erro de estimativa: o erro padrão é a distância média entre os valores observados e a linha de regressão. Neste exemplo, os valores observados desviam em média 5.861 unidades da linha de regressão.
A seguinte tabela que nos interessa intitula-se Coeficientes :
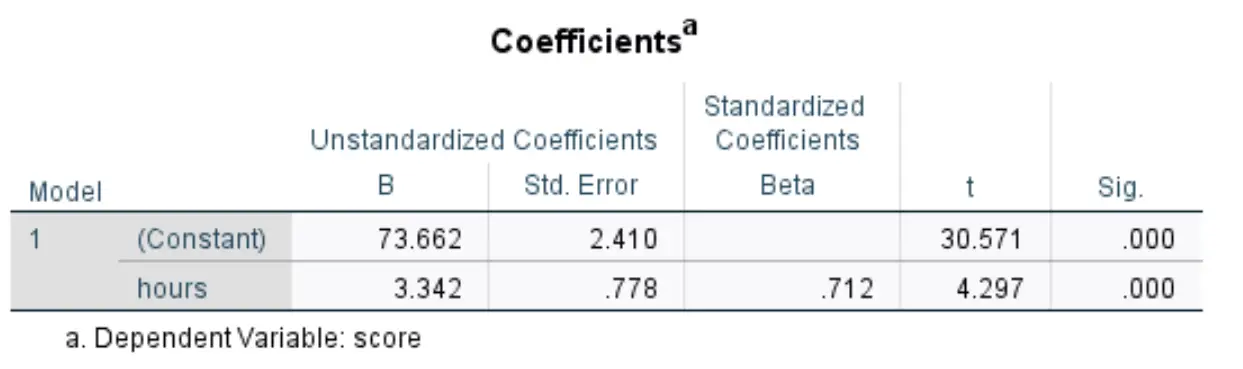
Veja como interpretar os números mais relevantes nesta tabela:
- B não padronizado (constante) : informa o valor médio da variável de resposta quando a variável preditora é zero. Neste exemplo, a nota média do exame é 73,662 quando as horas cursadas são zero.
- B não padronizado (horas): indica a mudança média na variável de resposta associada a um aumento de uma unidade na variável preditora. Neste exemplo, cada hora adicional estudada está associada a um aumento de 3.342 na nota do exame, em média.
- Sig (horas): Este é o valor p associado à estatística de teste durante horas. Neste caso, como este valor é inferior a 0,05, podemos concluir que a variável preditora horas é estatisticamente significativa.
Finalmente, podemos formar uma equação de regressão usando os valores de constante e horas . Neste caso, a equação seria:
Nota estimada do exame = 73,662 + 3,342*(horas)
Podemos usar esta equação para encontrar a nota estimada de um aluno no exame, com base no número de horas estudadas.
Por exemplo, um aluno que estuda 3 horas deverá obter nota 83.688 no exame:
Nota estimada do exame = 73,662 + 3,342*(3) = 83,688
Etapa 4: relatar os resultados.
Finalmente, queremos resumir os resultados da nossa regressão linear simples. Aqui está um exemplo de como fazer isso:
Uma regressão linear simples foi realizada para quantificar a relação entre horas estudadas e nota no exame. Uma amostra de 20 alunos foi utilizada na análise.
Os resultados mostraram que existe uma relação estatisticamente significativa entre as horas estudadas e a nota do exame (t = 4,297, p < 0,000) e que as horas estudadas representaram 50,6% da variabilidade explicada na nota do exame. o exame.
A equação de regressão acabou sendo:
Nota estimada do exame = 73,662 + 3,342*(horas)
Cada hora adicional estudada está associada a um aumento de 3.342 na nota do exame, em média.
Recursos adicionais
Os tutoriais a seguir explicam como executar outras tarefas comuns no SPSS:
Como realizar regressão linear múltipla no SPSS
Como realizar regressão quadrática no SPSS
Como realizar regressão logística no SPSS