Como realizar regressão linear múltipla no spss

A regressão linear múltipla é um método que podemos usar para compreender a relação entre duas ou mais variáveis explicativas e uma variável de resposta.

Este tutorial explica como realizar regressão linear múltipla no SPSS.

Exemplo: Regressão Linear Múltipla no SPSS

Suponha que queiramos saber se o número de horas gastas estudando e o número de exames práticos realizados afetam a nota que um aluno recebe em um determinado exame. Para explorar isso, podemos realizar regressão linear múltipla usando as seguintes variáveis:

Variáveis explicativas:

• Horas estudadas
• Exames preparatórios aprovados

Resposta variável:

• Resultado de exame

Use as etapas a seguir para realizar esta regressão linear múltipla no SPSS.

Passo 1: Insira os dados.

Insira os seguintes dados para o número de horas estudadas, exames preparatórios realizados e resultados de exames recebidos para 20 alunos:

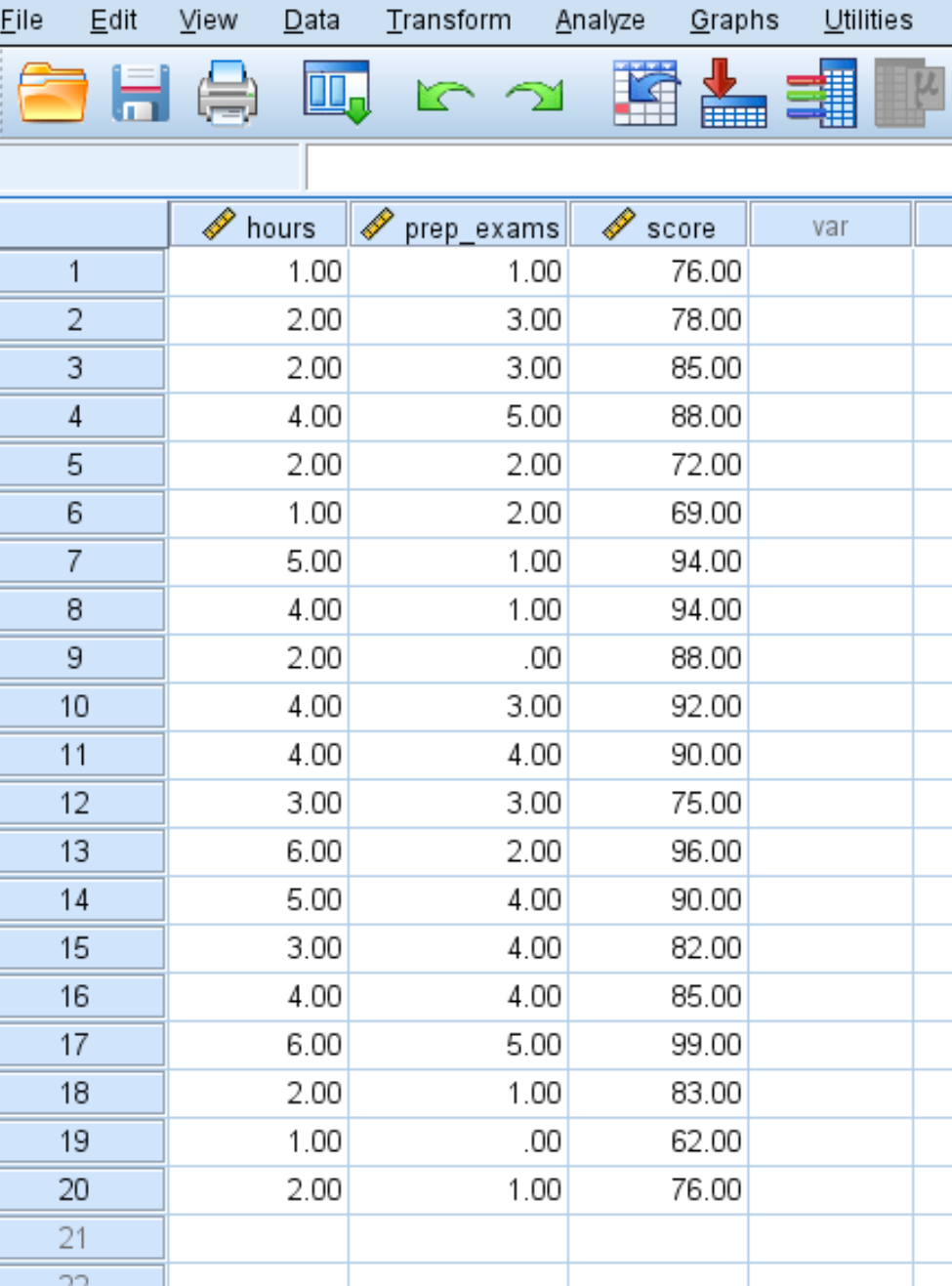
Etapa 2: Execute a regressão linear múltipla.

Clique na guia Analisar , depois em Regressão e depois em Linear :

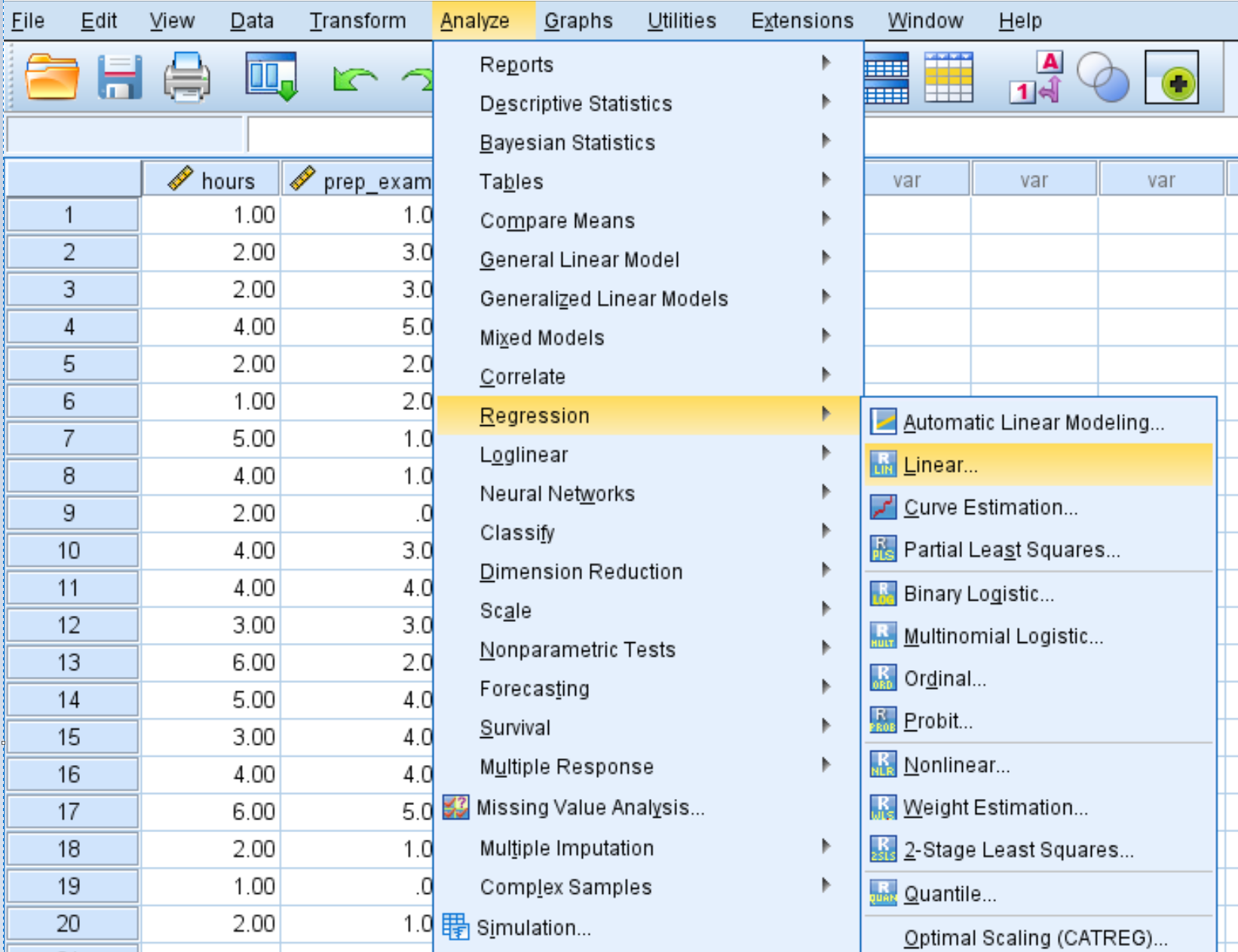
Arraste a pontuação variável para a caixa denominada Dependente. Arraste as variáveis horas e prep_exams para a caixa denominada Independent(es). Em seguida, clique em OK .

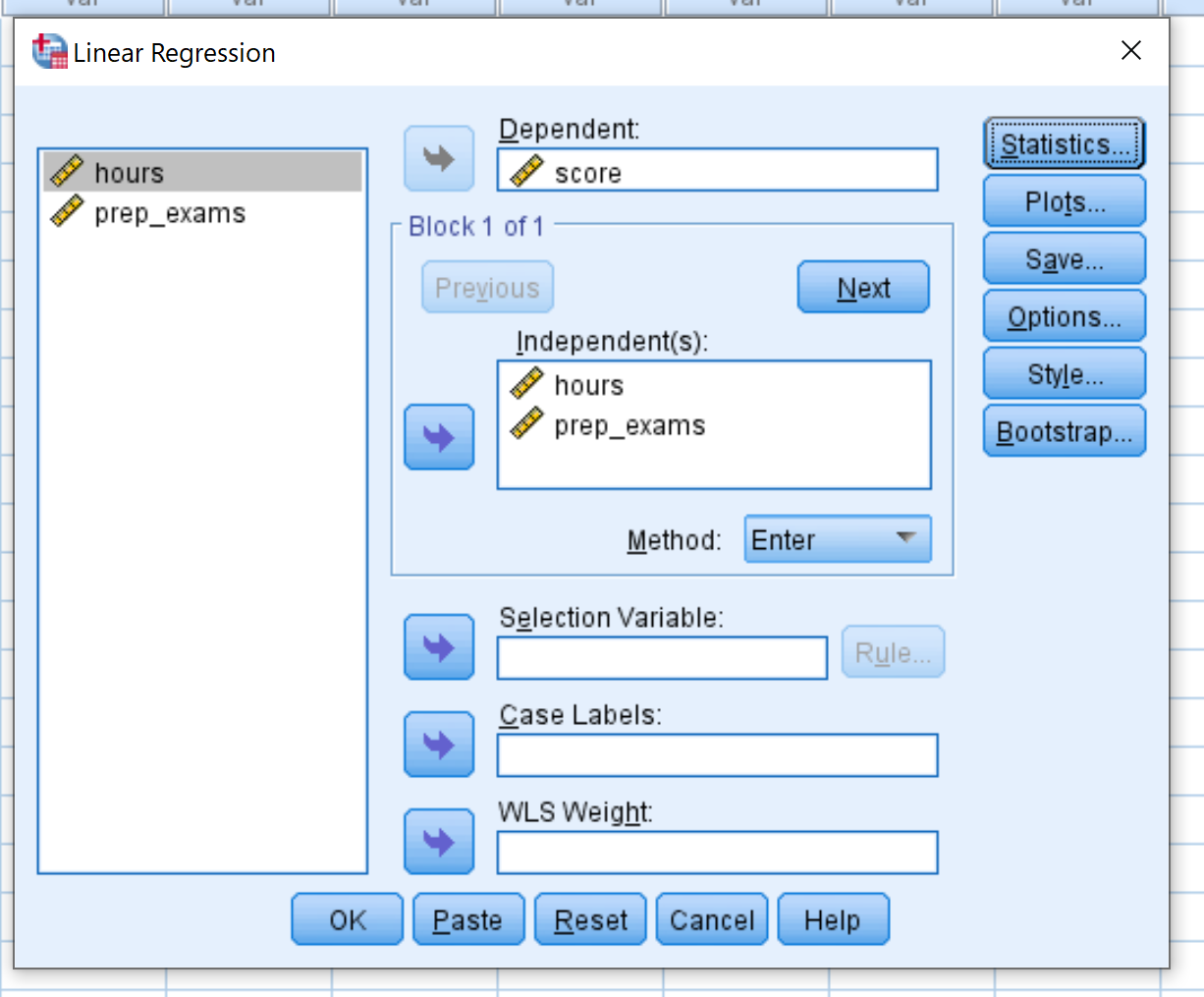
Etapa 3: interprete o resultado.

Depois de clicar em OK , os resultados da regressão linear múltipla aparecerão em uma nova janela.

A primeira tabela que nos interessa chama-se Resumo do Modelo :

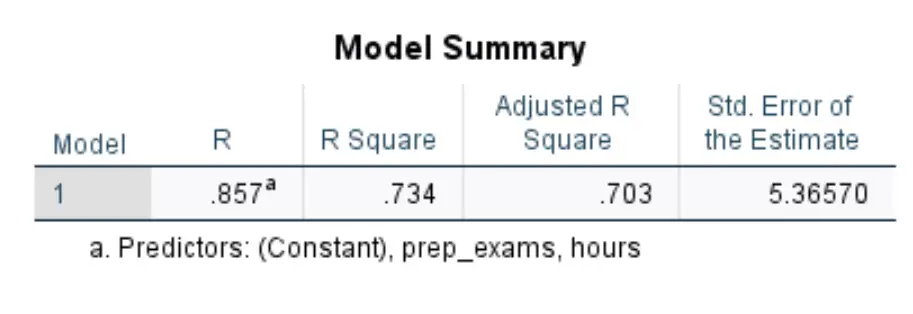
Veja como interpretar os números mais relevantes nesta tabela:

• R Quadrado: Esta é a proporção da variância na variável resposta que pode ser explicada pelas variáveis explicativas. Neste exemplo, 73,4% da variação nas notas dos exames pode ser explicada pelas horas estudadas e pelo número de exames preparatórios realizados.
• Padrão. Erro de estimativa: o erro padrão é a distância média entre os valores observados e a linha de regressão. Neste exemplo, os valores observados desviam-se em média 5,3657 unidades da linha de regressão.

A próxima tabela que nos interessa chama-se ANOVA :

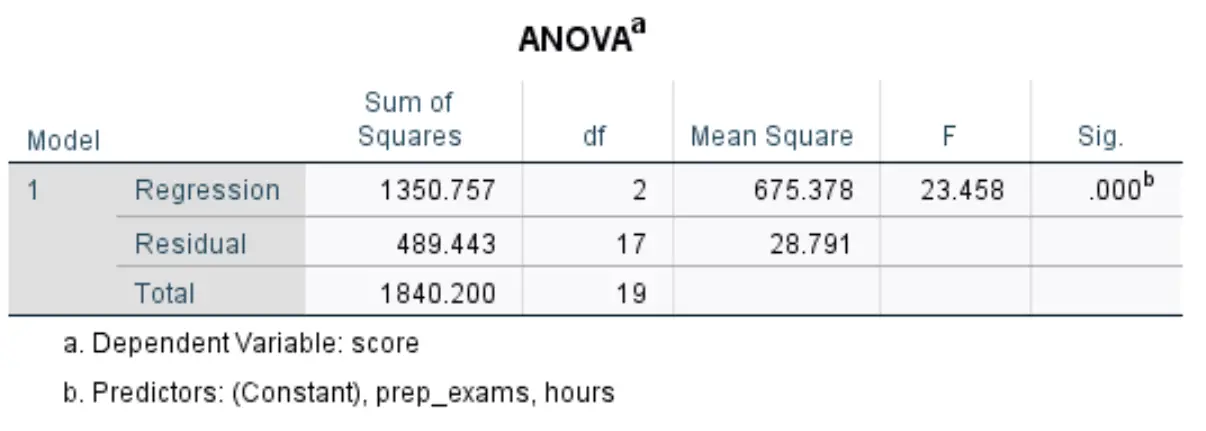
Veja como interpretar os números mais relevantes nesta tabela:

• F: Esta é a estatística F geral para o modelo de regressão, calculada como Regressão Quadrática Média / Residual Quadrático Médio.
• Sig: Este é o valor p associado à estatística F geral. Isto nos diz se o modelo de regressão como um todo é estatisticamente significativo ou não. Por outras palavras, diz-nos se as duas variáveis explicativas combinadas têm uma associação estatisticamente significativa com a variável resposta. Nesse caso, o valor p é igual a 0,000, o que indica que as variáveis explicativas, horas estudadas e exames preparatórios realizados, possuem associação estatisticamente significativa com o resultado do exame.

A seguinte tabela que nos interessa intitula-se Coeficientes :

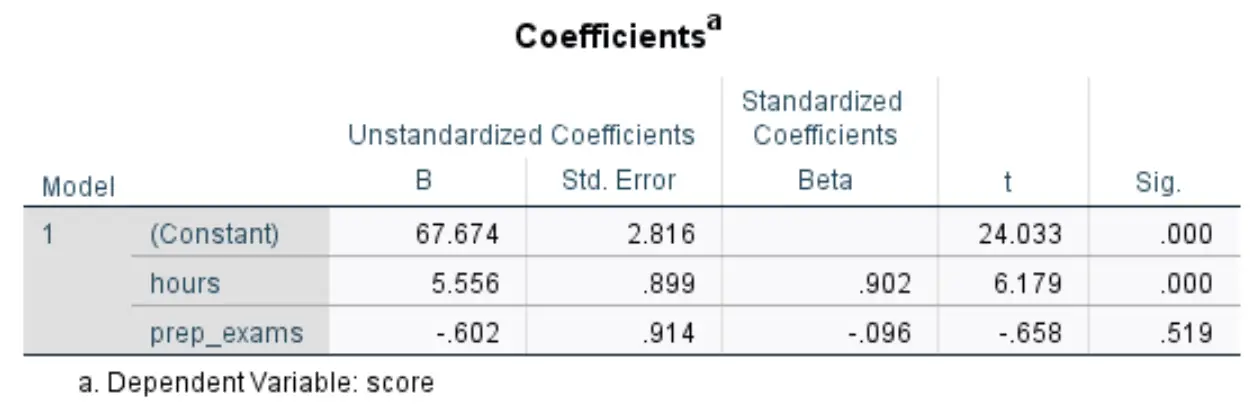
Veja como interpretar os números mais relevantes nesta tabela:

• B não padronizado (constante): nos diz o valor médio da variável resposta quando ambas as variáveis preditoras são zero. Neste exemplo, a pontuação média do exame é 67.674 quando as horas estudadas e os exames preparatórios realizados são ambos zero.
• B não padronizado (horas): Isso nos diz a mudança média nas notas dos exames associada a um aumento de uma unidade nas horas de estudo, assumindo que o número de exames preparatórios realizados permanece constante. Nesse caso, cada hora adicional de estudo está associada a um aumento de 5.556 pontos na nota do exame, assumindo que o número de simulados realizados permanece constante.
• B não padronizado (prep_exams): Isso nos diz a mudança média na pontuação do exame associada a um aumento de uma unidade nos exames preparatórios realizados, assumindo que o número de horas estudadas permanece constante. Neste caso, cada exame preparatório adicional realizado está associado a uma diminuição de 0,602 pontos na nota do exame, assumindo que o número de horas estudadas se mantém constante.
• Assinatura. (horas): Este é o valor p da variável explicativa horas . Como este valor (0,000) é inferior a 0,05, podemos concluir que as horas estudadas têm associação estatisticamente significativa com as notas dos exames.
• Assinatura. (prep_exams): Este é o valor p da variável explicativa prep_exams . Dado que este valor (0,519) não é inferior a 0,05, não podemos concluir que o número de exames preparatórios realizados tenha associação estatisticamente significativa com o resultado do exame.

Finalmente, podemos formar uma equação de regressão usando os valores mostrados na tabela para constante , horas e prep_exams . Neste caso, a equação seria:

Pontuação estimada do exame = 67,674 + 5,556*(horas) – 0,602*(prep_exams)

Podemos usar essa equação para encontrar a pontuação estimada de um aluno no exame, com base no número de horas de estudo e no número de exames práticos que ele fez. Por exemplo, um aluno que estuda 3 horas e faz 2 exames preparatórios deve receber nota 83,1 no exame:

Nota estimada do exame = 67,674 + 5,556*(3) – 0,602*(2) = 83,1

Nota: Como a variável explicativa dos exames preparatórios não foi considerada estatisticamente significativa, podemos decidir retirá-la do modelo e, em vez disso, realizar uma regressão linear simples usando as horas estudadas como única variável explicativa.