Coeficiente de correlação de pearson
Este artigo explica o que é o coeficiente de correlação de Pearson (ou coeficiente de correlação linear) e para que é utilizado. Você descobrirá como calcular o coeficiente de correlação de Pearson juntamente com um exercício passo a passo. Além disso, você pode encontrar o valor do Coeficiente de Correlação de Pearson de qualquer conjunto de dados com a calculadora online no final.
Qual é o coeficiente de correlação de Pearson?
O coeficiente de correlação de Pearson , também chamado de coeficiente de correlação linear ou simplesmente coeficiente de correlação , é uma medida estatística que indica a relação entre duas variáveis.
Para calcular o coeficiente de correlação de Pearson entre duas variáveis, deve-se dividir a covariância dessas variáveis pela raiz quadrada do produto de suas variâncias.
Assim, o coeficiente de correlação de Pearson tenta quantificar a dependência linear entre duas variáveis aleatórias quantitativas. A priori, avaliar numericamente a correlação entre variáveis é complicado porque é difícil determinar que o par de variáveis está mais correlacionado entre se, como em pues, o objetivo do coeficiente de correlação de Pearson é avaliar a relação entre variáveis para poder compare entre eles.
O valor do índice de correlação de Pearson está entre -1 e +1 inclusive. Veremos a seguir como é interpretado o valor do coeficiente de correlação de Pearson.
Fórmula do coeficiente de correlação de Pearson
O coeficiente de correlação de Pearson de duas variáveis estatísticas é igual ao quociente entre a covariância das variáveis e a raiz quadrada do produto da variância de cada variável.
Portanto, a fórmula para cálculo do coeficiente de correlação de Pearson é a seguinte:
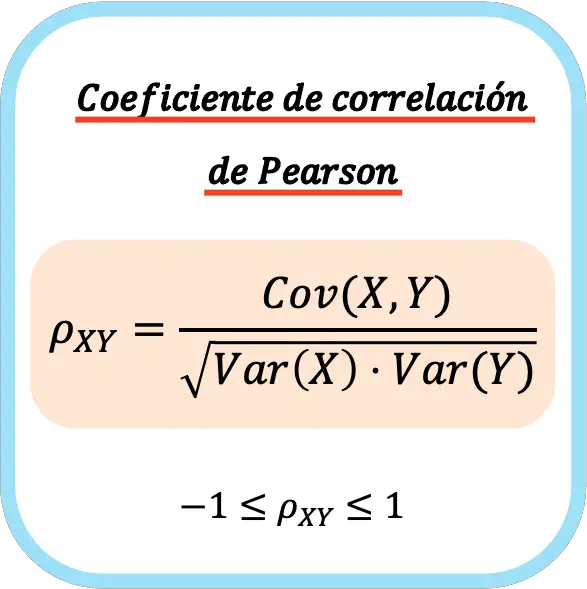
👉 Você pode usar a calculadora abaixo para calcular o coeficiente de correlação de Pearson para qualquer conjunto de dados.
Quando o coeficiente de correlação de Pearson é calculado sobre uma população, é geralmente expresso pela letra grega ρ. Mas quando o coeficiente é calculado em relação a uma amostra, a letra r é geralmente usada como símbolo.
Lembre-se que para determinar o coeficiente de correlação de Pearson é fundamental que você saiba calcular a covariância entre duas variáveis e a variância de uma variável. Além disso, você precisa entender o que significam essas medidas estatísticas. Portanto, antes de continuar a explicação, recomenda-se a leitura dos dois artigos a seguir:
Exemplo de cálculo do coeficiente de correlação de Pearson
Considerando a definição do coeficiente de correlação de Pearson e sua fórmula, segue abaixo um exemplo passo a passo para você ver como ele é calculado.
- Calcule o coeficiente de correlação de Pearson entre as duas variáveis contínuas a seguir:

Antes de calcular o coeficiente de correlação de Pearson, representaremos o conjunto de dados em um gráfico de dispersão para analisar a relação entre as duas variáveis:
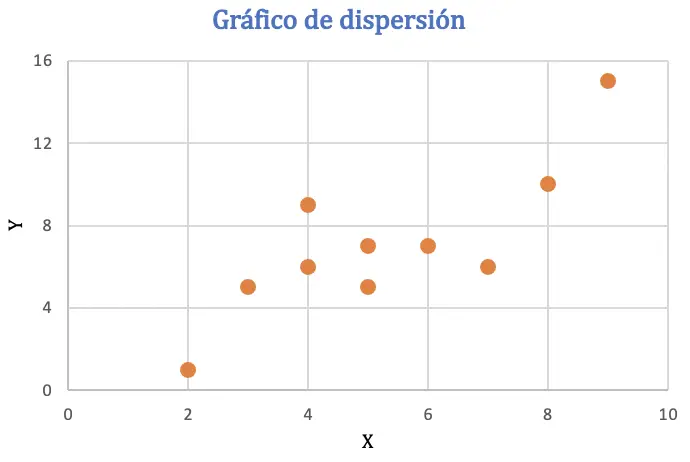
A partir do gráfico de dispersão, pode-se inferir que os dados podem ter uma tendência positiva, ou seja, quando uma variável aumenta de valor, a outra variável também aumenta. Para verificar a correlação, encontraremos o coeficiente de Pearson.
A primeira coisa a fazer é encontrar a média aritmética de cada variável separadamente, que equivale à soma total dos dados dividida pelo número de observações.
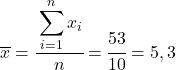
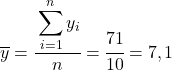
Agora que sabemos a média de cada variável, precisamos adicionar as seguintes colunas à tabela de dados:
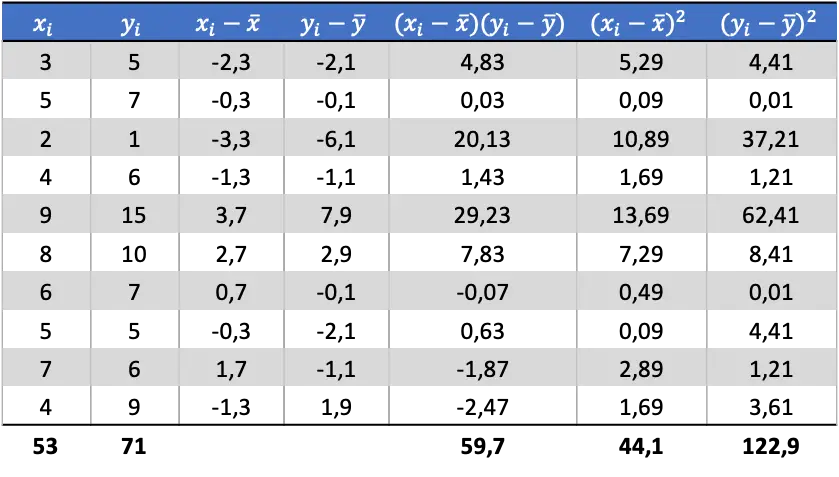
A partir dos dados calculados na tabela, determinamos os valores de covariância e variância (se você não lembra como isso foi feito, há dois links acima onde isso é explicado detalhadamente):
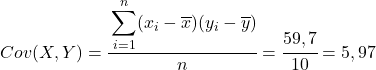
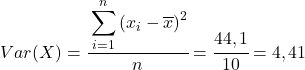
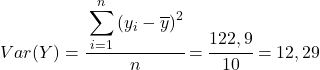
Por fim, basta aplicar a fórmula do coeficiente de correlação de Pearson para obter o seu valor:
![]()
O coeficiente de correlação de Pearson tem um valor muito próximo de 1, o que significa que estas duas variáveis têm uma correlação positiva bastante forte.
Como você viu, para determinar o coeficiente de correlação de Pearson é muito útil utilizar programas como o Excel para realizar cálculos de colunas mais rapidamente.
Calculadora do coeficiente de correlação de Pearson
Insira um conjunto de dados estatísticos na calculadora a seguir para calcular o coeficiente de correlação de Pearson entre duas variáveis. Você precisa separar os pares de dados, para que na primeira caixa existam apenas os valores de uma variável e na segunda caixa existam apenas os valores da segunda variável.
Os dados devem ser separados por espaço e inseridos usando o ponto final como separador decimal.
Interpretando o Coeficiente de Correlação de Pearson
Nesta seção veremos como interpretar o coeficiente de correlação de Pearson, pois não basta saber seu valor, mas é preciso saber analisar seu significado.
Assim a interpretação do coeficiente de correlação de Pearson depende do seu valor:
- r=-1 : as duas variáveis têm uma correlação negativa perfeita, portanto podemos traçar uma linha com inclinação negativa na qual todos os pontos se ligam.
- -1<r<0 : a correlação entre as duas variáveis é negativa, portanto quando uma variável aumenta a outra diminui. Quanto mais próximo o valor estiver de -1, mais negativamente relacionadas serão as variáveis.
- r=0 : a correlação entre as duas variáveis é muito fraca, na verdade, a relação linear entre elas é zero. Isso não significa que as variáveis sejam independentes, pois poderiam ter uma relação não linear.
- 0<r<1 : a correlação entre as duas variáveis é positiva, quanto mais próximo o valor estiver de +1, mais forte será a relação entre as variáveis. Nesse caso, uma variável tende a aumentar de valor quando a outra também aumenta.
- r=1 : as duas variáveis possuem correlação positiva perfeita, ou seja, possuem relação linear positiva.
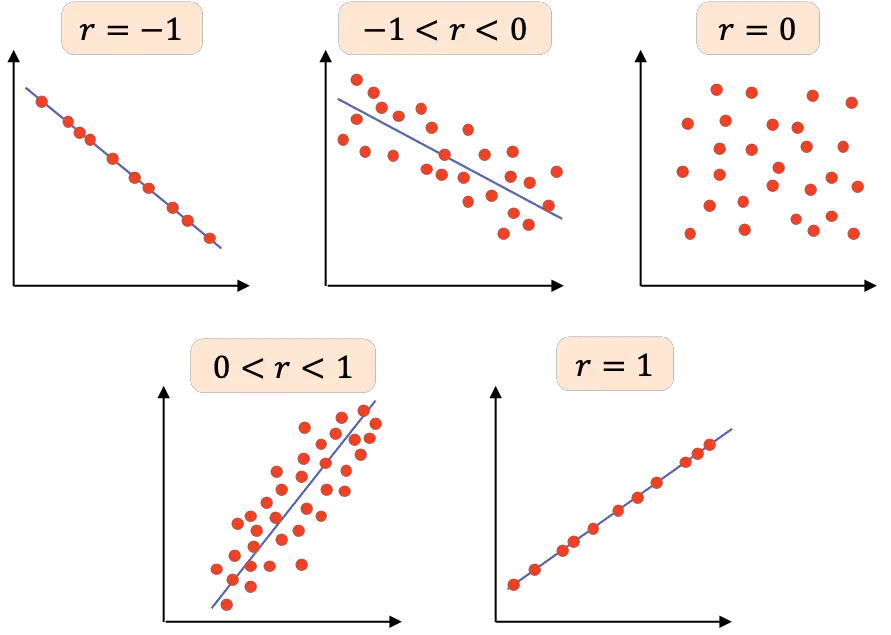
Em resumo, é apresentada a seguinte tabela com as diferentes interpretações do coeficiente de correlação de Pearson:
| Valor | Interpretação |
|---|---|
| r=-1 | Correlação negativa perfeita. |
| -1<r<0 | Correlação negativa: quanto mais próxima a correlação estiver de -1, mais forte ela será. |
| r=0 | Correlação linear zero. |
| 0<r<1 | Correlação positiva: quanto mais próxima a correlação estiver de +1, mais forte ela será. |
| r=1 | Correlação positiva perfeita. |
Tenha em mente que mesmo que exista uma relação entre duas variáveis, isso não significa que haja causalidade entre elas, ou seja, a correlação entre duas variáveis não significa que a mudança em uma variável seja a causa da mudança da variável. outra variável.
Por exemplo, se descobrirmos que existe uma relação positiva entre a produção de dois hormônios diferentes no corpo, não é necessário que um aumento em um hormônio leve a um aumento no outro hormônio. Pode ser que o corpo produza ambos os hormônios porque precisa de ambos para combater uma doença e, portanto, aumenta os níveis de ambos simultaneamente, caso em que a causa seria a doença. Para determinar se existe uma ligação causal entre os dois hormônios, mais estudos devem ser realizados.