Como realizar anova de medidas repetidas no spss

Uma ANOVA de medidas repetidas é usada para determinar se há ou não uma diferença estatisticamente significativa entre as médias de três ou mais grupos em que os mesmos sujeitos aparecem em cada grupo.

Este tutorial explica como realizar uma ANOVA de medidas repetidas unilaterais no SPSS.

Exemplo: ANOVA de medidas repetidas no SPSS

Os pesquisadores querem saber se quatro medicamentos diferentes causam tempos de reação diferentes. Para testar isso, eles mediram o tempo de reação de cinco pacientes a quatro medicamentos diferentes. Como cada paciente é medido com cada um dos quatro medicamentos, usaremos uma ANOVA de medidas repetidas para determinar se o tempo médio de reação difere entre os medicamentos.

Conclua as etapas a seguir para realizar ANOVA de medidas repetidas no SPSS.

Passo 1: Insira os dados.

Insira os seguintes dados, que mostram o tempo de resposta (em segundos) de cinco pacientes aos quatro medicamentos:

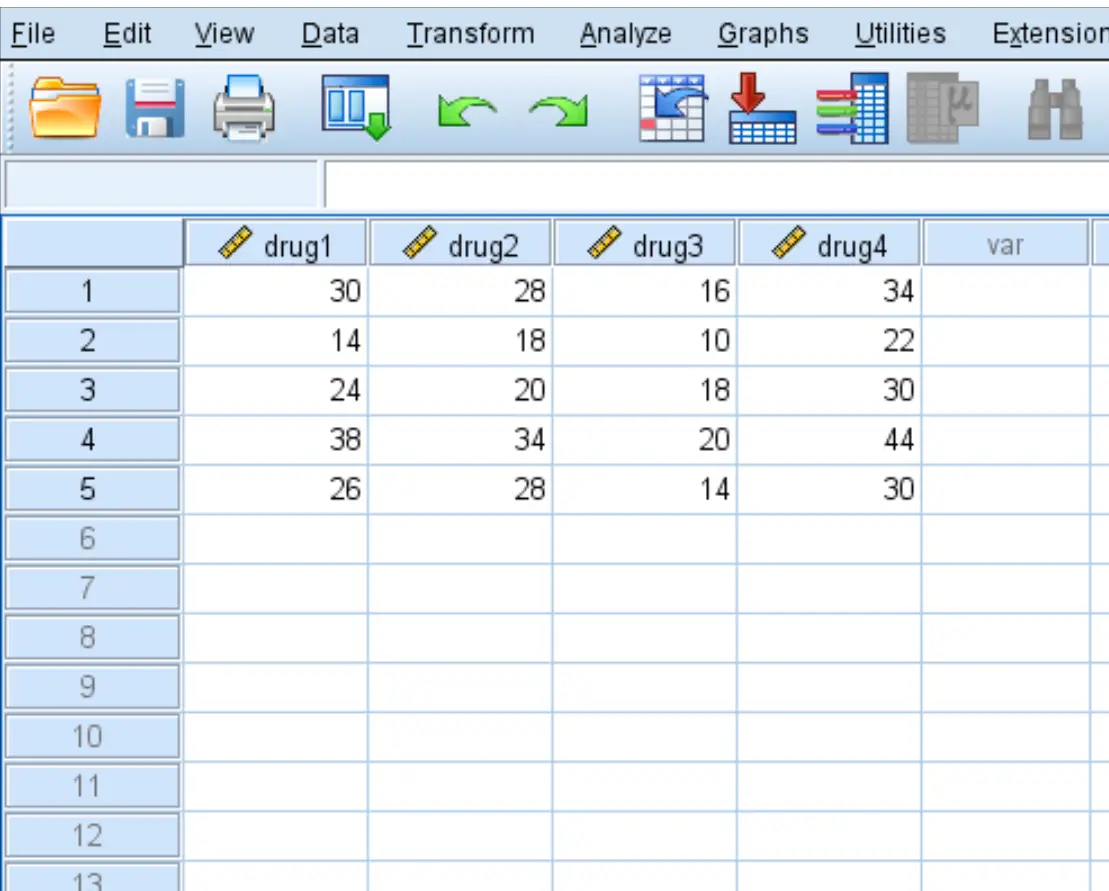
Etapa 2: Execute uma ANOVA de medidas repetidas.

Clique na guia Analisar , depois em Modelo Linear Geral e em Medições Repetidas :

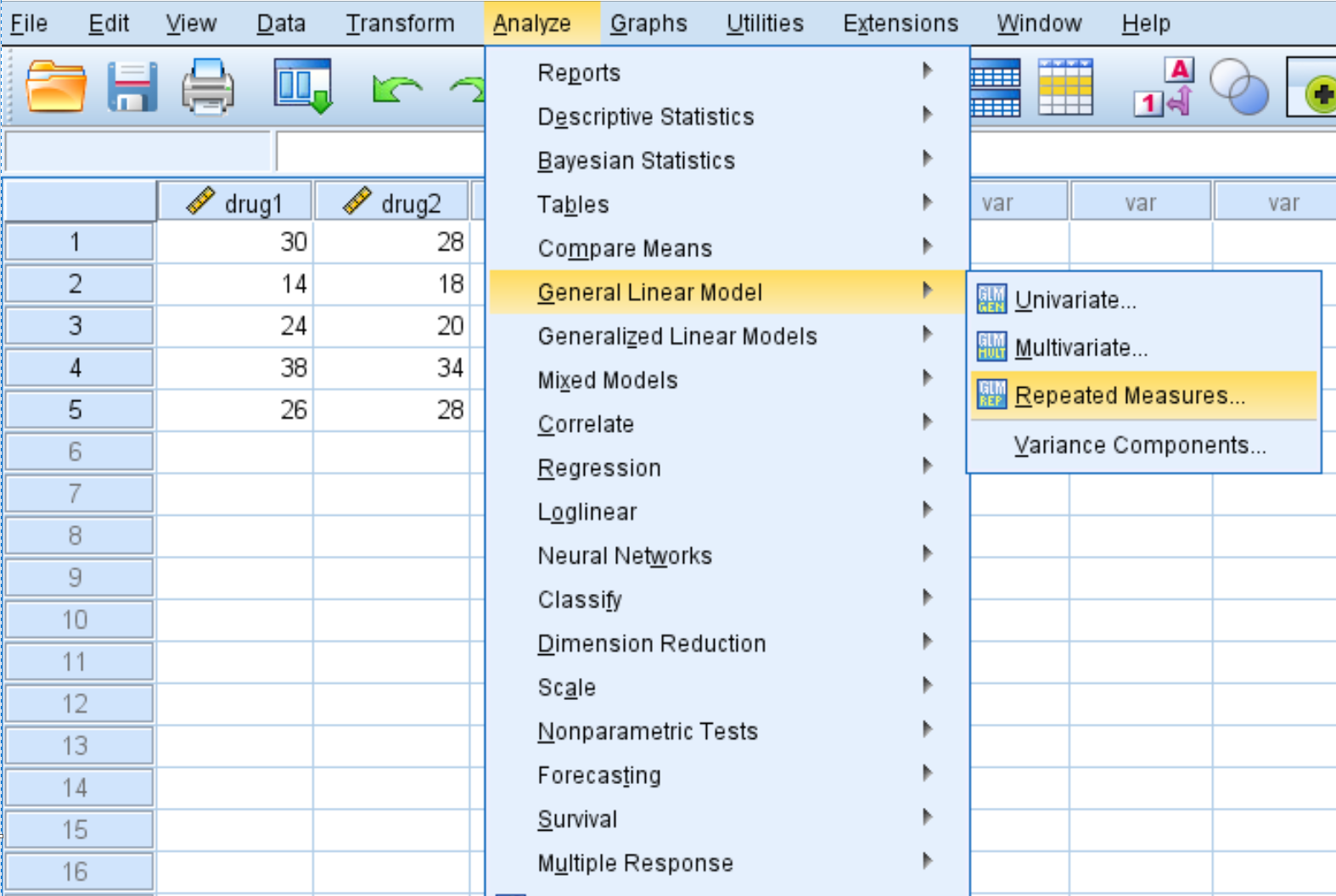
Na nova janela que aparece, insira o nome do medicamento para o fator intra-sujeito. Digite 4 para o número de níveis (já que cada sujeito do estudo testou 4 medicamentos diferentes) e clique em Adicionar . Digite ResponseTime para Measure Name e clique em Add . Por fim, clique em Definir .

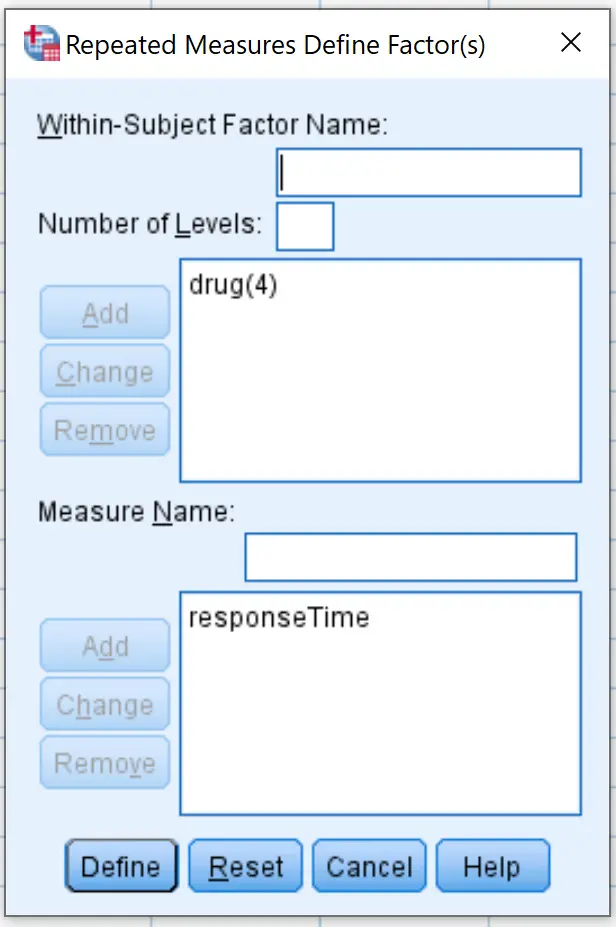
Na nova janela que aparece, arraste cada uma das quatro variáveis do medicamento para a área denominada Variáveis dentro dos assuntos :

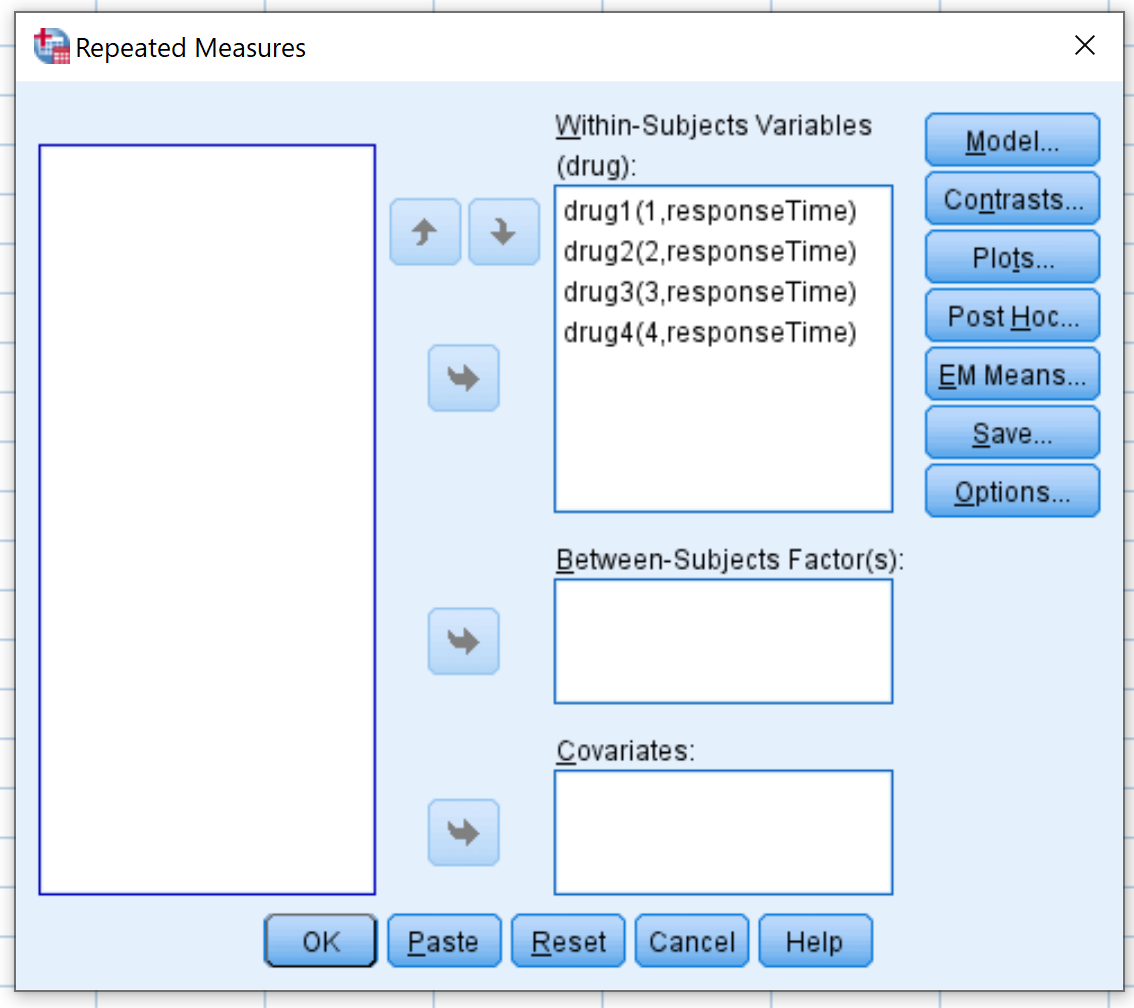
Em seguida, clique em Plotagens . Arraste a variável medicamento para a área denominada Eixo Horizontal . Em seguida, clique em Adicionar . Em seguida, clique em Continuar .

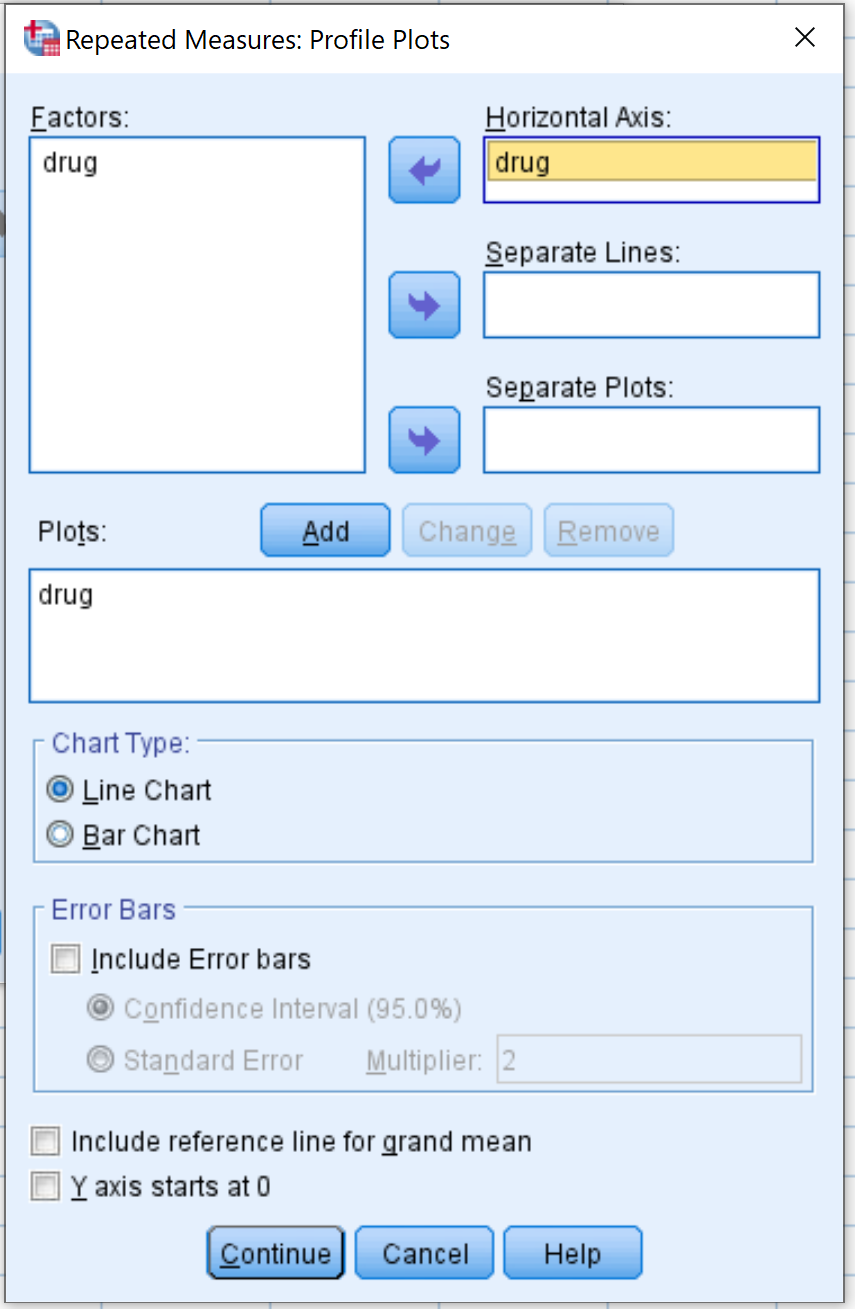
Em seguida, clique em Meios EM . Arraste a variável droga para a caixa chamada Show Means For . Em seguida, marque a caixa ao lado de Comparar efeitos principais e selecione Bonferroni no menu suspenso. Em seguida, clique em Continuar .

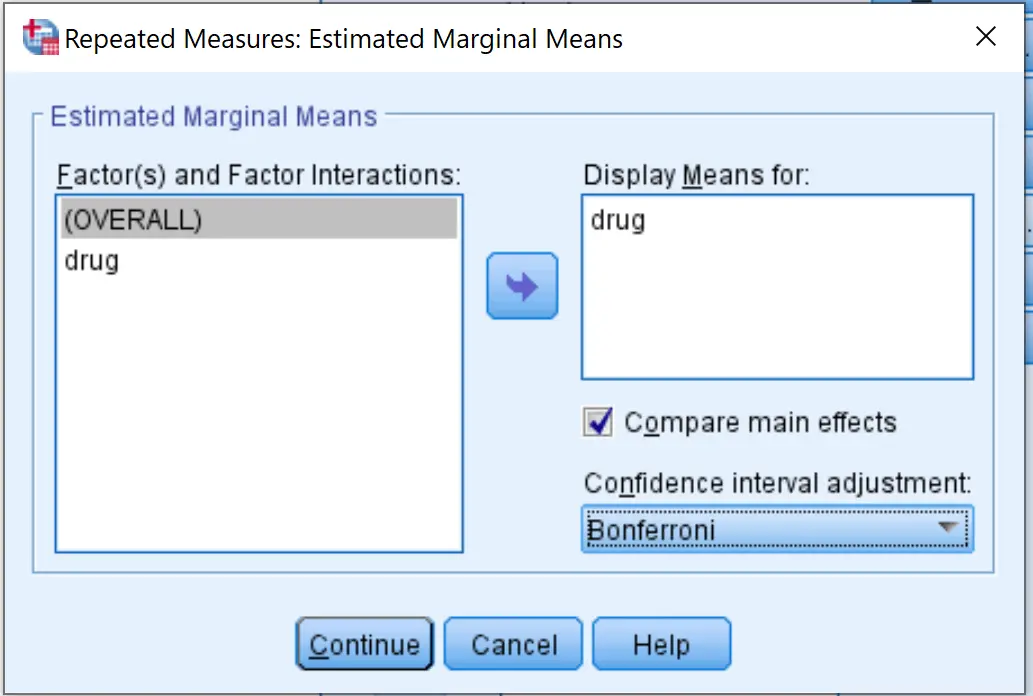
Por fim, clique em OK .

Etapa 2: interprete os resultados.

Depois de clicar em OK , os resultados da ANOVA de medidas repetidas aparecerão. Veja como interpretar o resultado:

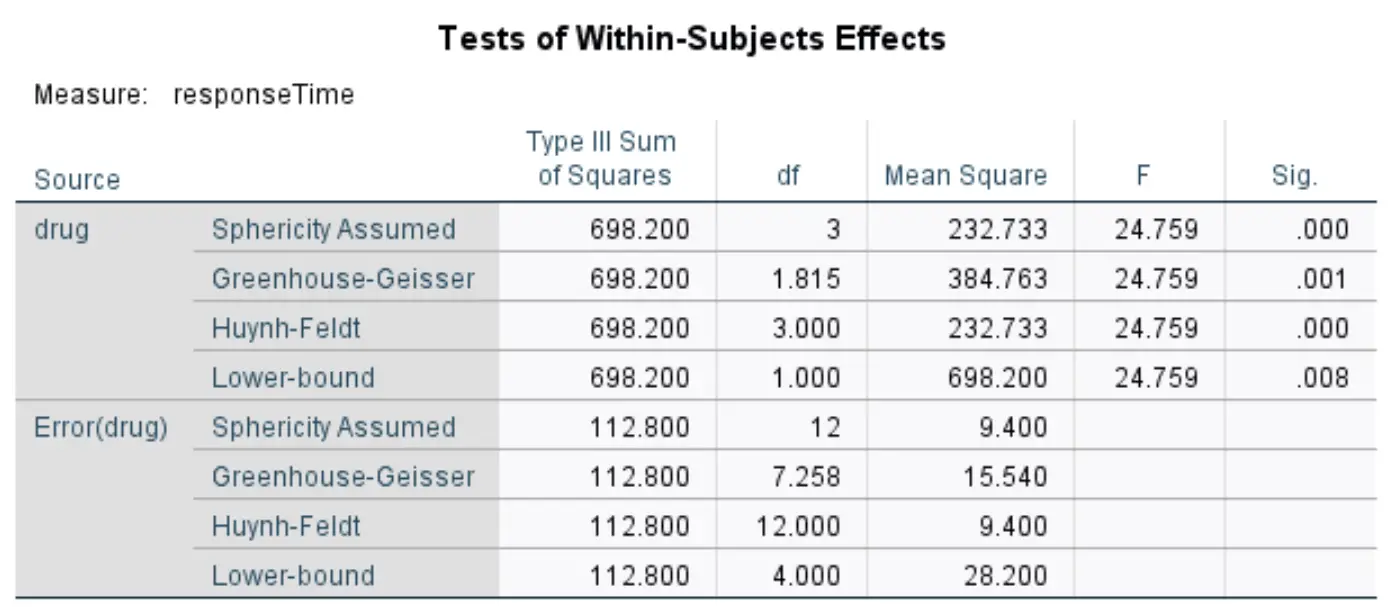
Testes de efeitos dentro dos assuntos

Esta tabela exibe a estatística F geral e o valor p correspondente da ANOVA de medidas repetidas. Geralmente usamos valores da linha denominada Greenhouse-Geisser .

De acordo com esta linha, a estatística F é 24,759 e o valor p correspondente é 0,001 . Como este valor de p é inferior a 0,05, podemos rejeitar a hipótese nula e concluir que existe uma diferença estatisticamente significativa nos tempos médios de resposta entre os quatro medicamentos.

Comparações por pares

Como rejeitamos a hipótese nula, isso significa que pelo menos duas médias de grupos são diferentes. Para determinar quais grupos de médias são diferentes, podemos usar esta tabela que mostra as comparações aos pares entre cada medicamento.

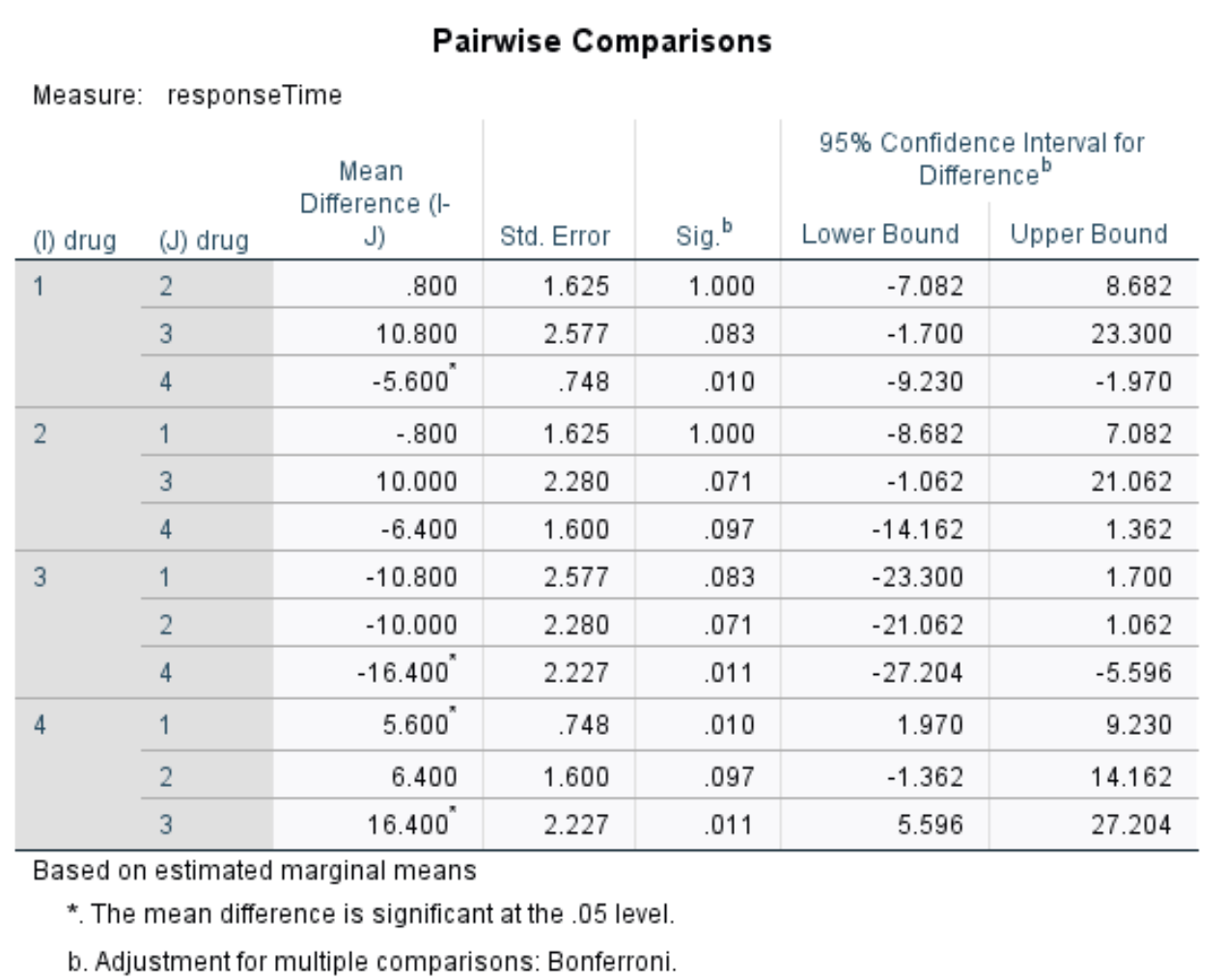
Na tabela podemos ver os valores p para as seguintes comparações:

• droga 1 versus droga 2 | valor p = 1.000
• droga 1 versus droga 3 | valor p = 0,083
• droga 1 versus droga 4 | valor p = 0,010
• droga 2 versus droga 3 | valor p = 0,071
• droga 2 versus droga 4 | valor p = 0,097
• droga 3 versus droga 4 | valor p = 0,011

Os únicos valores de p inferiores a 0,05 são para medicamento 1 versus medicamento 4 e medicamento 3 versus medicamento 4. Todas as outras comparações apresentam valores de p superiores a 0,05.

Gráfico de médias marginais estimadas

Este gráfico exibe os tempos médios de resposta estimados para cada medicamento. No gráfico, podemos ver claramente que os tempos de resposta variaram significativamente entre os quatro medicamentos diferentes:

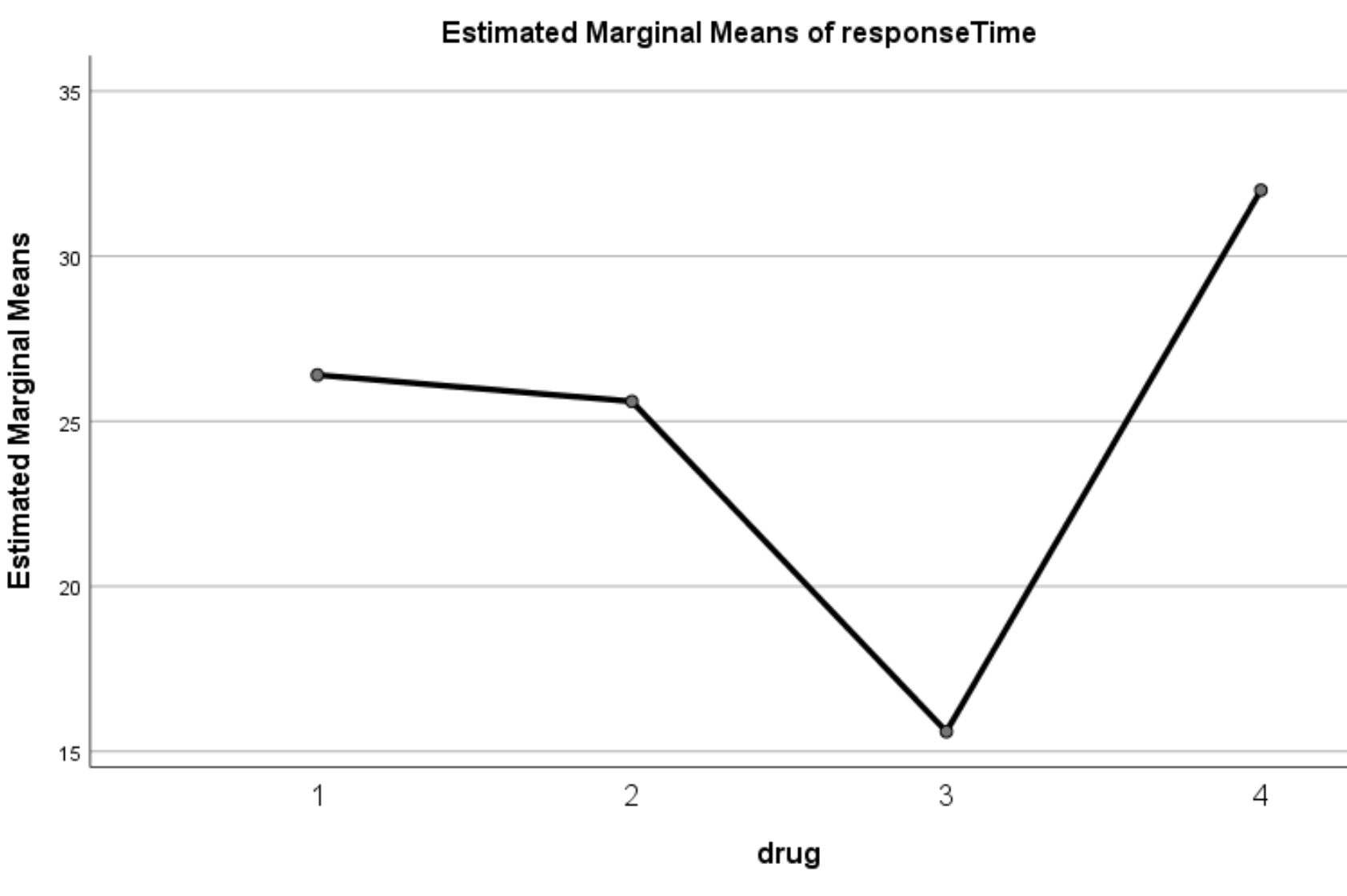
Etapa 3: relatar os resultados.

Finalmente, podemos relatar os resultados da ANOVA de medidas repetidas. Aqui está um exemplo de como fazer isso:

Uma ANOVA unidirecional de medidas repetidas foi realizada para determinar se o tempo médio de reação dos pacientes diferia entre quatro medicamentos diferentes.

Uma ANOVA unidirecional para medidas repetidas revelou que o tipo de medicação utilizada resultou em diferenças estatisticamente significativas no tempo de resposta (F = 24,75887, p = 0,001).

O teste de Bonferroni para comparações múltiplas revelou que houve uma diferença estatisticamente significativa nos tempos de resposta entre os pacientes que tomaram o medicamento 1 e o medicamento 4, bem como o medicamento 3 e o medicamento 4.