Como calcular pontuações z no spss
Uma pontuação z nos diz quantos desvios padrão um determinado valor está da média.
A pontuação z de um determinado valor é calculada da seguinte forma:
pontuação z = (x – μ) / σ
Ouro:
- x: valor individual
- μ: média populacional
- σ: desvio padrão populacional
Este tutorial explica como calcular pontuações z no SPSS.
Relacionado: Como interpretar pontuações Z
Como calcular pontuações Z no SPSS
Suponha que temos o seguinte conjunto de dados que mostra a renda anual (em milhares) de 15 pessoas:
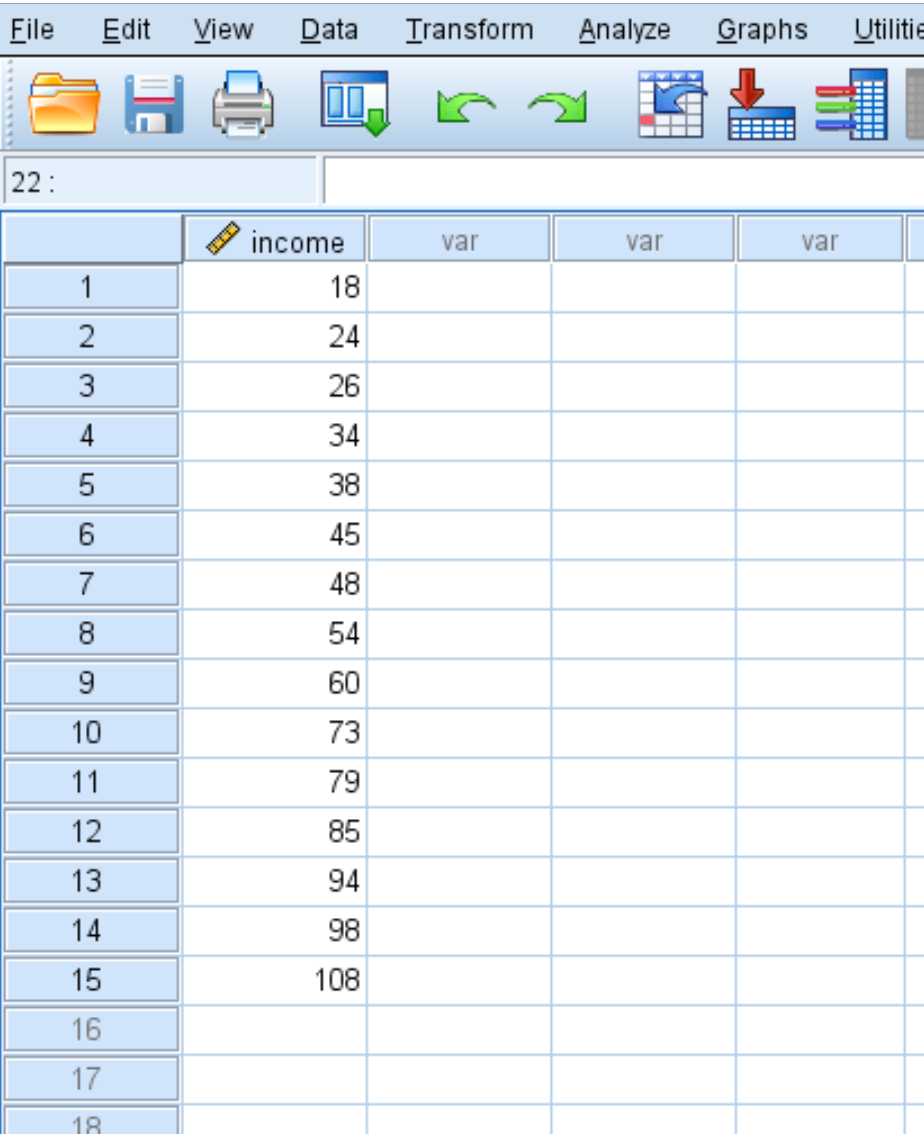
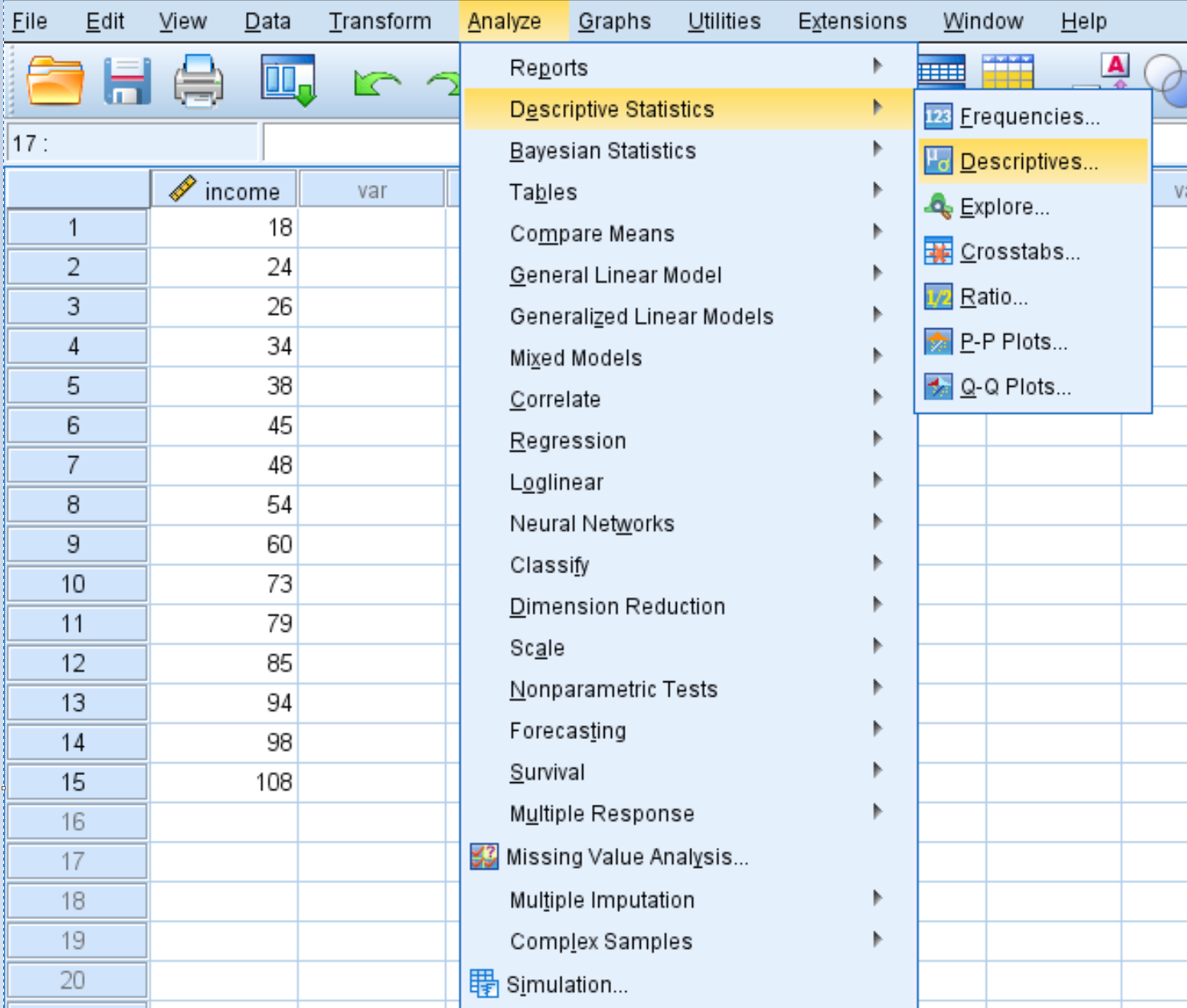
Para calcular pontuações z para cada valor no conjunto de dados, clique na guia Analisar , depois em Estatísticas Descritivas e em Descritivos :
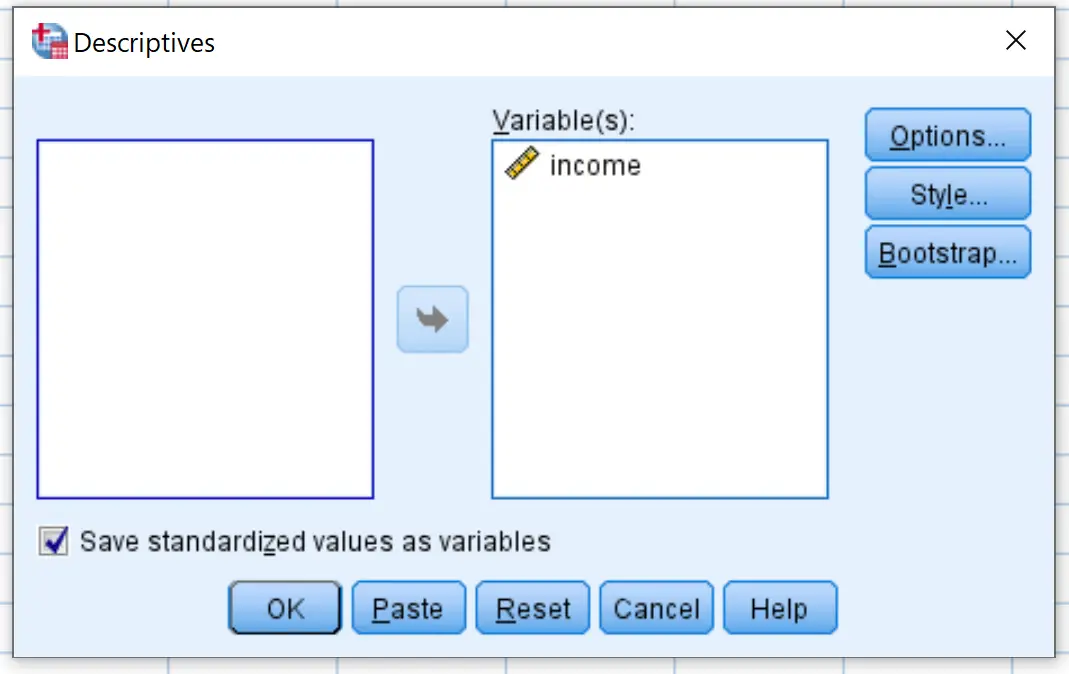
Na nova janela que aparece, arraste a variável de renda para a caixa denominada Variável(es).
Certifique-se de que a caixa ao lado de Salvar valores padronizados como variáveis esteja marcada e clique em OK .
Depois de clicar em OK , o SPSS produzirá uma tabela de estatísticas descritivas para o seu conjunto de dados:
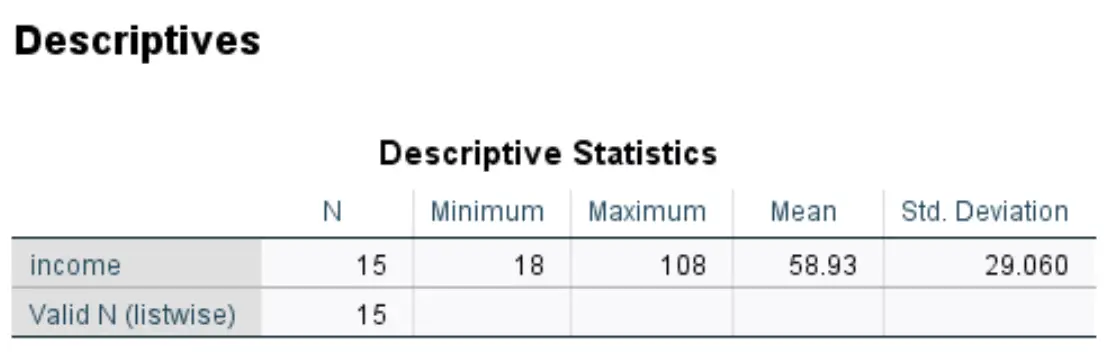
O SPSS também produzirá uma nova coluna de valores que exibe o z-score para cada um dos valores originais em seu conjunto de dados:
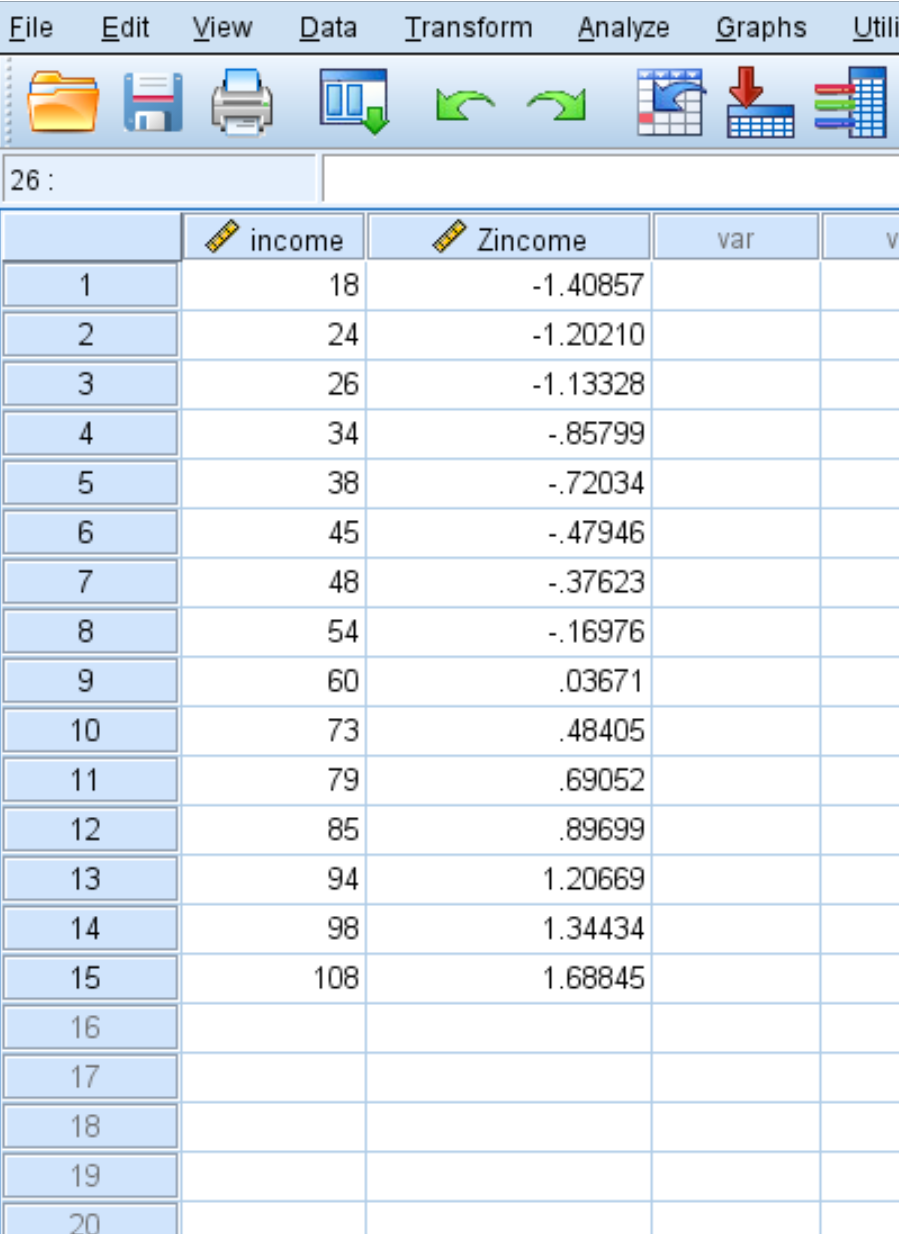
Cada uma das pontuações z é calculada usando a fórmula z = (x – μ) / σ
Por exemplo, a pontuação z para o valor da renda de 18 é:
z = (18 – 58,93) / 29,060 = -1,40857 .
As pontuações Z para todos os outros valores de dados são calculadas da mesma maneira.
Como interpretar pontuações Z
Lembre-se de que uma pontuação z simplesmente nos diz quantos desvios padrão um valor está da média.
Uma pontuação z pode ser positiva, negativa ou igual a zero:
- Uma pontuação z positiva indica que um determinado valor está acima da média.
- Uma pontuação z negativa indica que um determinado valor está abaixo da média.
- Uma pontuação z de zero indica que um determinado valor é igual à média.
No nosso exemplo, descobrimos que a média foi 58,93 e o desvio padrão foi 29,060.
Portanto, o primeiro valor em nosso conjunto de dados foi 18, que teve uma pontuação z de (18 – 58,93) / 29,060 = -1,40857 .
Isso significa que o valor “18” é 1,40857 desvios padrão inferior à média.
Por outro lado, o último valor em nossos dados foi 108, o que correspondeu a um escore z de (108 – 58,93) / 29,060 = 1,68845 .
Isso significa que o valor “108” está 1,68845 desvios padrão acima da média.
Recursos adicionais
Os tutoriais a seguir explicam como executar outras tarefas comuns no SPSS:
Como calcular estatísticas descritivas para variáveis no SPSS
Como calcular um resumo de cinco dígitos no SPSS
Como identificar outliers no SPSS