O que é uma distribuição bimodal?
Uma distribuição bimodal é uma distribuição de probabilidade com dois modos.
Freqüentemente usamos o termo “moda” em estatísticas descritivas para nos referirmos ao valor mais comum em um conjunto de dados, mas neste caso o termo “moda” refere-se a um máximo local em um gráfico.
Ao visualizar uma distribuição bimodal, você notará dois “picos” distintos que representam esses dois modos.
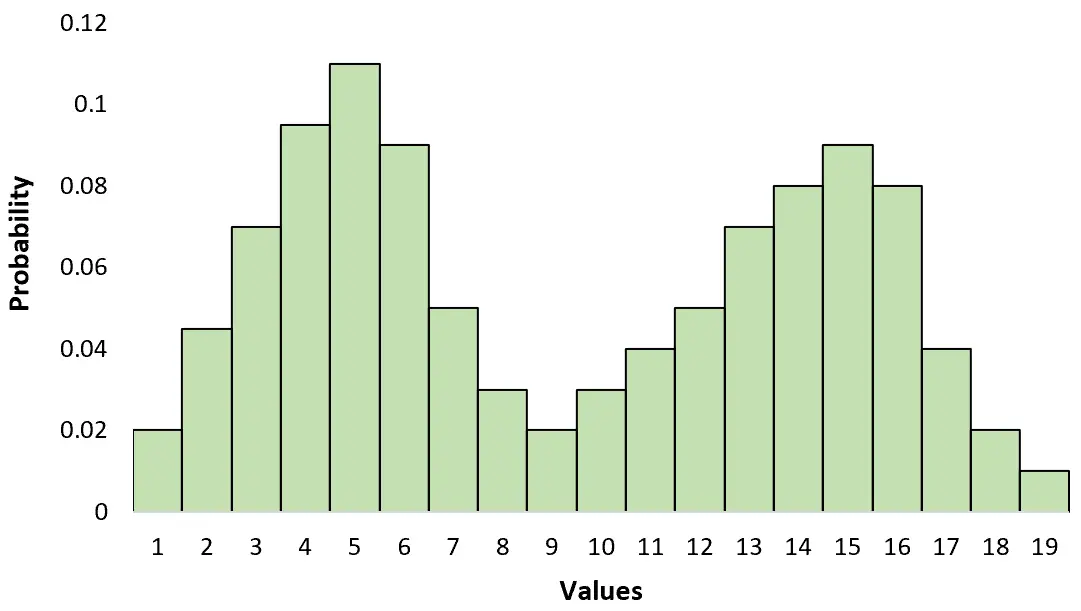
Isso é diferente de uma distribuição unimodal que possui apenas um pico:
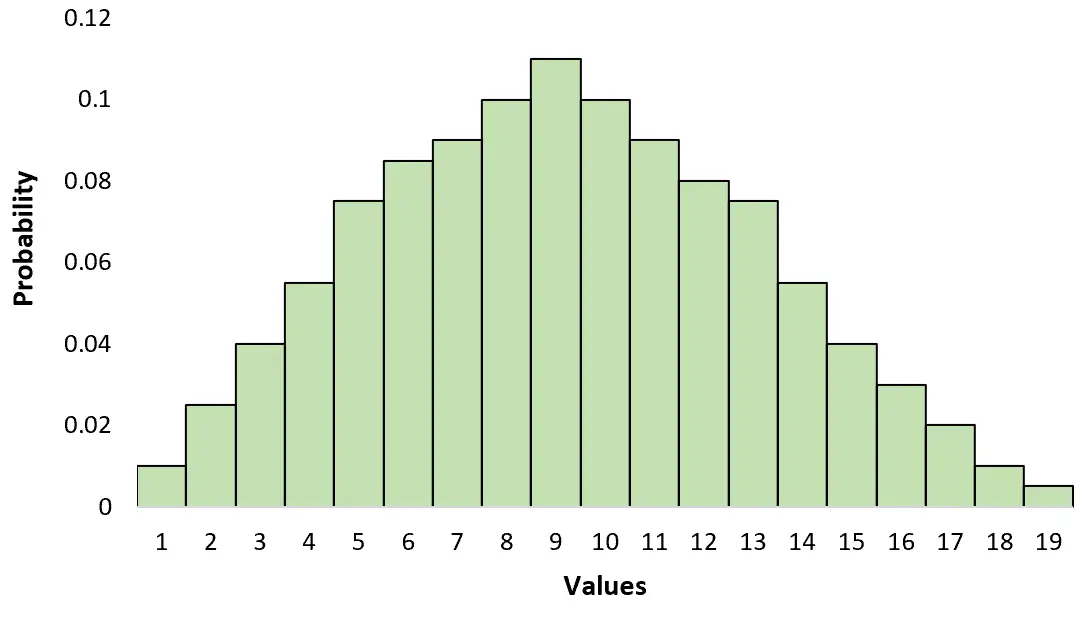
Você pode lembrar a diferença entre os dois lembrando:
- “bi” = dois
- “unido” = um
Embora a maioria dos cursos de estatística utilize distribuições unimodais como a distribuição normal para explicar diferentes tópicos, as distribuições bimodais aparecem com bastante frequência na prática, por isso é útil saber como reconhecê-las e interpretá-las.
Nota: Uma distribuição bimodal é um tipo específico de distribuição multimodal .
Exemplos de distribuições bimodais
Aqui estão alguns exemplos de distribuições bimodais:
Exemplo nº 1: Horário de pico do restaurante
Se você criasse um gráfico para visualizar a distribuição horária dos clientes de um determinado restaurante, provavelmente descobriria que ele segue uma distribuição bimodal com pico no horário do almoço e outro pico no horário do jantar:
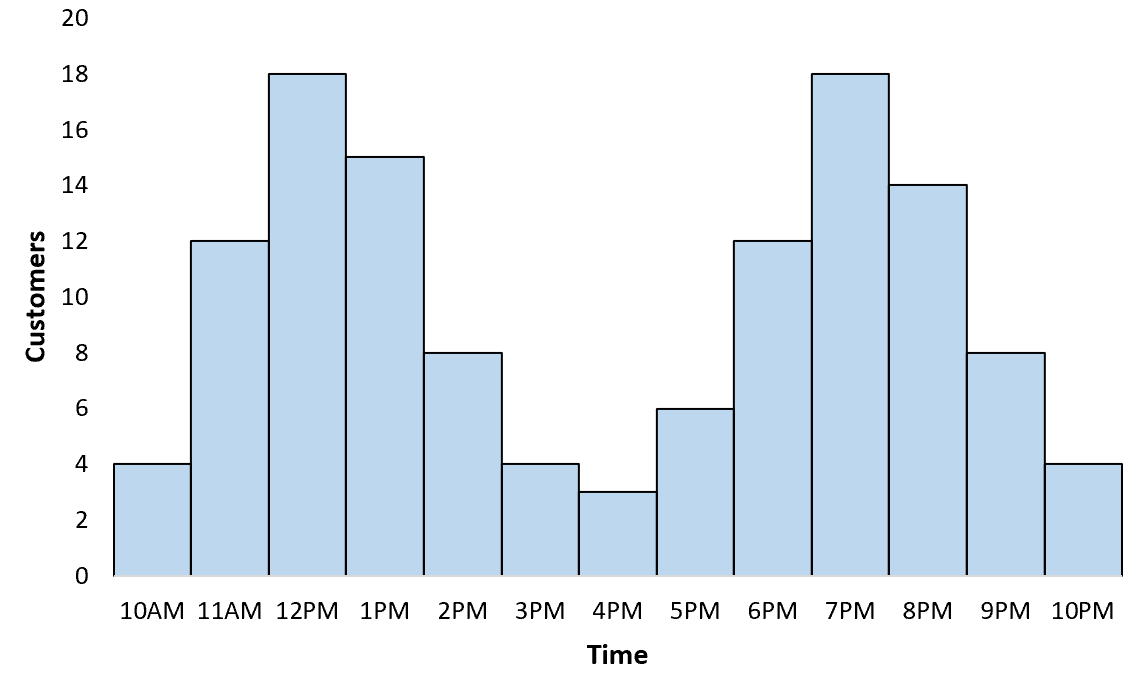
Exemplo não. 2: Altura média de duas espécies de plantas
Suponha que você ande por um campo e meça a altura de diferentes plantas. Sem perceber, você está medindo o tamanho de duas espécies diferentes: uma bem grande e outra bem pequena. Se você criasse um gráfico para visualizar a distribuição de alturas, ele seguiria uma distribuição bimodal:
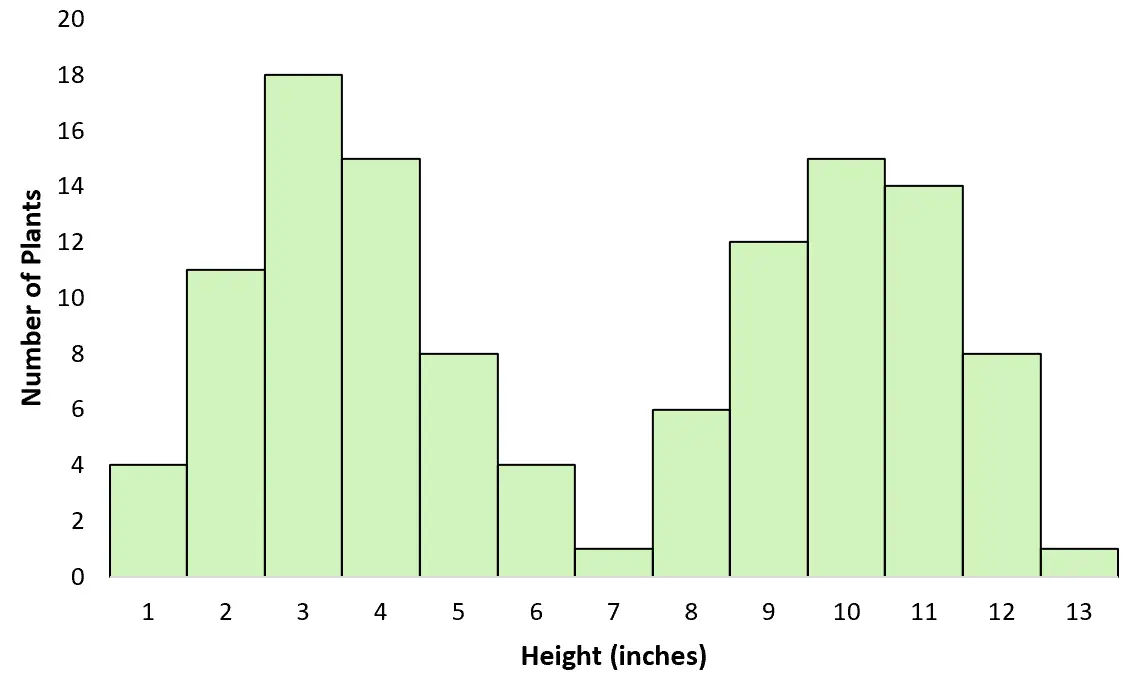
Exemplo #3: resultados de exames
Suponha que um professor dê um exame para sua turma de alunos. Alguns alunos estudaram para o exame, outros não. Quando o professor cria um gráfico de resultados de exames, ele segue uma distribuição bimodal com um pico em torno das notas baixas para os alunos que não estudaram e outro pico em torno das notas altas para os alunos que estudaram:
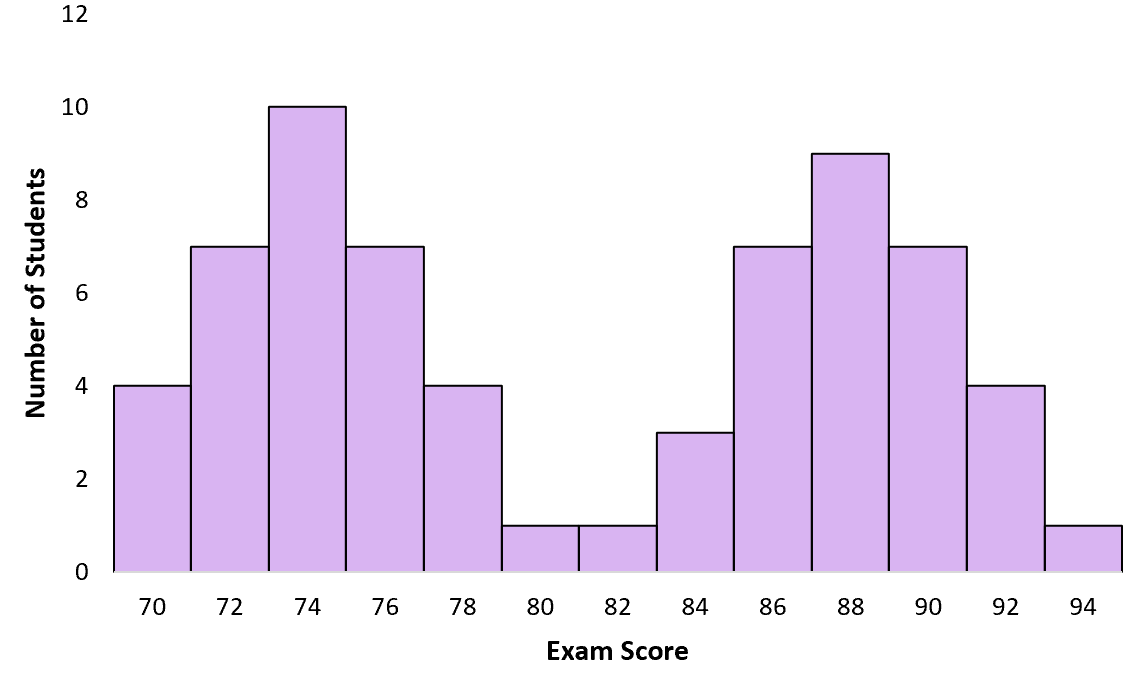
O que causa distribuições bimodais?
Geralmente há duas coisas que causam distribuições bimodais:
1. Alguns fenómenos subjacentes.
As distribuições bimodais ocorrem frequentemente devido a certos fenômenos subjacentes.
Por exemplo, o número de clientes que visitam um restaurante a cada hora segue uma distribuição bimodal, uma vez que as pessoas tendem a comer nos restaurantes em dois horários distintos: almoço e jantar. Este comportamento humano subjacente é a origem da distribuição bimodal.
2. Dois grupos diferentes agrupados.
Distribuições bimodais também podem ocorrer quando você simplesmente analisa dois grupos diferentes de coisas sem perceber.
Por exemplo, se você medir a altura das plantas em um determinado campo sem perceber que duas espécies diferentes estão crescendo no mesmo campo, você verá uma distribuição bimodal ao criar um gráfico.
Como analisar distribuições bimodais
Freqüentemente descrevemos distribuições usando a média ou mediana porque isso nos dá uma ideia de onde está o “centro” da distribuição.
Infelizmente, não é útil saber a média e a mediana para uma distribuição bimodal. Por exemplo, a nota média do exame dos alunos no exemplo acima é 81:
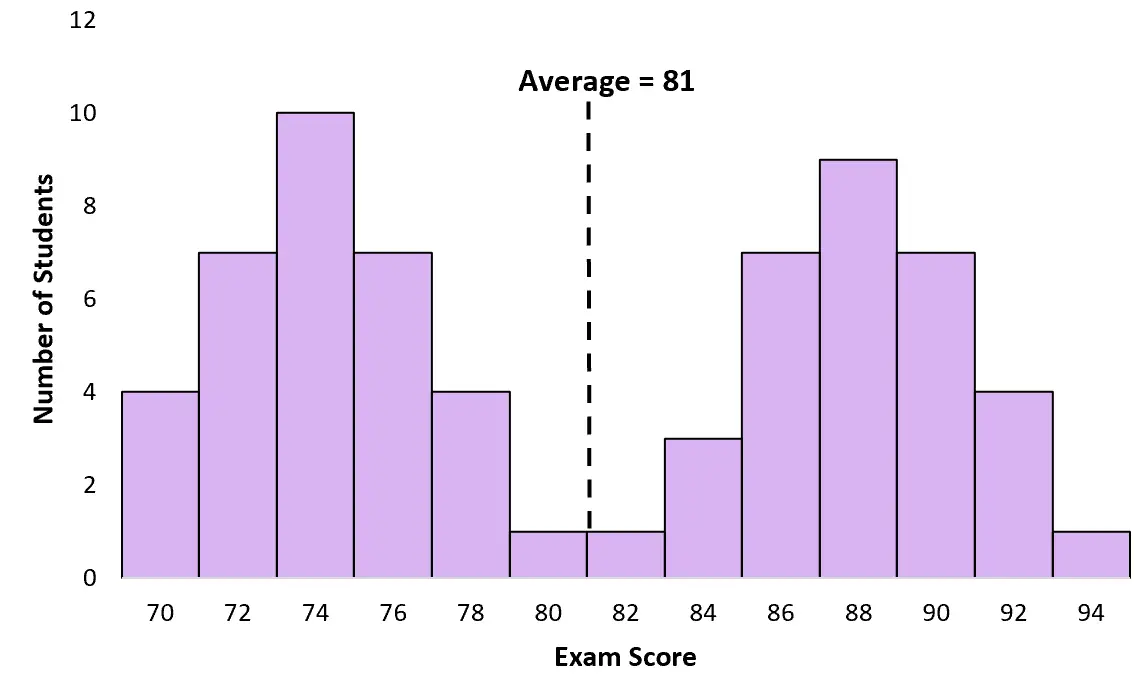
No entanto, muito poucos alunos obtiveram pontuações próximas de 81. Neste caso, a média é enganadora. A maioria dos alunos obteve pontuação em torno de 74 ou 88.
A melhor maneira de analisar e interpretar distribuições bimodais é simplesmente dividir os dados em dois grupos distintos e depois analisar o centro e a distribuição de cada grupo.
Por exemplo, podemos dividir os resultados dos exames em “pontuações baixas” e “pontuações altas” e então encontrar a média e o desvio padrão para cada grupo.
Se você estiver compartilhando os resultados de uma análise e seus dados seguirem uma distribuição bimodal, é útil criar um histograma como os mostrados acima para que seu público possa ver claramente que a distribuição tem dois “picos” distintos e que só faz faz sentido analisar cada pico separadamente, em vez de como um grande conjunto de dados.