Matriz de correlação

Neste artigo você descobrirá o que é uma matriz de correlação, qual é sua fórmula e como interpretar uma matriz de correlação. Além disso, você poderá ver um exemplo concreto de interpretação de uma matriz de correlação.

O que é uma matriz de correlação?

A matriz de correlação é uma matriz que contém na posição i,j o coeficiente de correlação entre as variáveis i e j .

Portanto, a matriz de correlação é uma matriz quadrada preenchida com unidades na diagonal principal e o elemento da linha i e da coluna j consiste no valor do coeficiente de correlação entre a variável i e a variável j .

A fórmula para a matriz de correlação é, portanto, a seguinte:

Ouro

é o coeficiente de correlação entre as variáveis

E

Assim, para encontrar a matriz de correlação de um conjunto de dados, é essencial que você saiba como o coeficiente de correlação é calculado. Caso você não se lembre, no link a seguir você descobrirá como fazer isso com uma calculadora online:

Uma propriedade do coeficiente de correlação é que para o seu cálculo não importa a ordem das variáveis, ou seja, o coeficiente de correlação

é equivalente a

Portanto, a matriz de correlação é simétrica.

Para que uma matriz de correlação seja significativa, o conjunto de dados estatísticos deve ter mais de duas variáveis. Caso contrário, seria suficiente determinar um único coeficiente de correlação e a matriz de correlação seria significativa.

Como fazer uma matriz de correlação

Dada a definição da matriz de correlação, vejamos como é criado esse tipo de matriz estatística:

1. Calcule o coeficiente de correlação de cada par de variáveis. Observe que a ordem das variáveis não altera o resultado, portanto só precisa ser calculado uma vez para cada par de variáveis.
2. Crie uma matriz quadrada da mesma dimensão que o número de variáveis na série de dados. Esta matriz será a matriz de correlação.
3. Coloque 1 em cada elemento da diagonal principal da matriz de correlação.
4. Coloque o coeficiente de correlação das variáveis i , j nas posições i , j e j , i .
5. Uma vez criada a matriz de correlação, resta apenas interpretar seus valores.

Lembre-se de que simplesmente executar a matriz de correlação não é suficiente, é necessário então interpretar seus valores e entender o que eles significam. A seção a seguir explica como interpretar uma matriz de correlação.

Interpretação da matriz de correlação

Para interpretar corretamente a matriz de correlação é necessário levar em consideração que o valor do coeficiente de correlação pode variar de -1 a +1:

• r=-1 : as duas variáveis têm uma correlação negativa perfeita, portanto podemos traçar uma linha com inclinação negativa na qual todos os pontos se ligam.
• -1<r<0 : a correlação entre as duas variáveis é negativa, portanto quando uma variável aumenta a outra diminui. Quanto mais próximo o valor estiver de -1, mais negativamente relacionadas serão as variáveis.
• r=0 : a correlação entre as duas variáveis é muito fraca, na verdade, a relação linear entre elas é zero. Isso não significa que as variáveis sejam independentes, pois poderiam ter uma relação não linear.
• 0<r<1 : a correlação entre as duas variáveis é positiva, quanto mais próximo o valor estiver de +1, mais forte será a relação entre as variáveis. Nesse caso, uma variável tende a aumentar seu valor quando a outra também aumenta.
• r=1 : as duas variáveis possuem uma correlação positiva perfeita, ou seja, possuem uma relação linear positiva.

Assim, para interpretar a matriz de correlação é necessário interpretar cada coeficiente de correlação e comparar os diferentes resultados.

Desta forma você poderá ver quais variáveis estão mais relacionadas entre si, quais variáveis são mais importantes, quais variáveis praticamente não têm relação entre si, etc.

Exemplo de matriz de correlação

Para entender completamente em que consiste a matriz de correlação e como ela é interpretada, nesta seção analisaremos um exemplo de matriz de correlação:

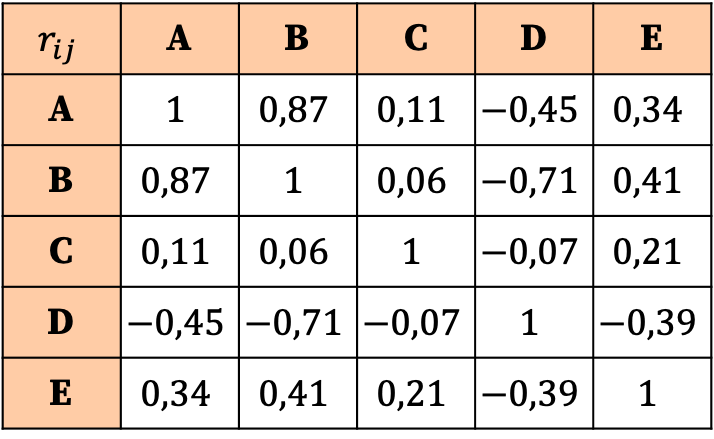
A interpretação da matriz de correlação é baseada nos valores dos coeficientes. Assim, podemos perceber que a correlação mais forte é a relação entre a variável A e a variável B, pois seu coeficiente correspondente é o maior (0,87).

Por outro lado, a variável C praticamente não tem correlação com nenhuma variável, pois todos os seus coeficientes são muito próximos de zero e, portanto, muito baixos. Assim, para simplificar a análise, poderíamos até considerar a retirada desta variável do estudo estatístico.

Da mesma forma, todas as relações da variável D com outras variáveis são negativas, o que significa que a correlação entre a variável D e outras variáveis é inversa. Isto não implica que a variável deva ser eliminada, apenas que a variável D está negativamente correlacionada.

Como você pode ver, a matriz de correlação é muito útil para resumir os dados e fazer uma análise geral da relação entre as diferentes variáveis do conjunto de dados.