Mediana
Este artigo explica o que é a mediana de um conjunto de dados e como encontrar a mediana para dados desagrupados e agrupados. Além disso, você pode calcular a mediana de qualquer série de dados com a calculadora online no final.
Qual é a mediana?
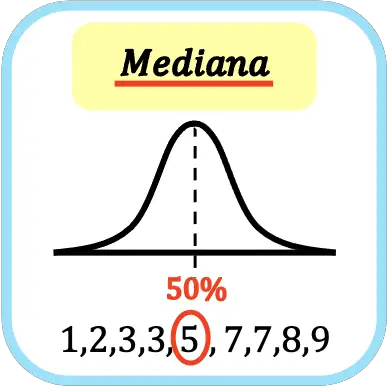
Nas estatísticas, a mediana é o valor médio de todos os dados ordenados do menor para o maior. Em outras palavras, a mediana divide o conjunto de dados ordenado em duas partes iguais.
A mediana é uma medida de posição central usada para descrever uma distribuição de probabilidade.
👉 Você pode usar a calculadora abaixo para calcular a mediana de qualquer conjunto de dados.
Em geral, o termo Self é frequentemente usado como símbolo do meio.
Outras medidas de posição central são média e moda, a seguir veremos as diferenças entre elas. Da mesma forma, as medidas de posição não central são quartis, quintis, decis, percentis, etc.
Deve-se notar que a mediana de um conjunto de dados coincide com o segundo quartil, quinto decil e 50º percentil.
Como calcular a mediana
O cálculo da mediana depende se o número total de dados é par ou ímpar:
- Se o número total de dados for ímpar , a mediana será o valor que fica bem no meio dos dados. Ou seja, o valor que está na posição (n+1)/2 dos dados ordenados.
- Se o número total de pontos de dados for par , a mediana será a média dos dois pontos de dados localizados no centro. Ou seja, a média aritmética dos valores que se encontram nas posições n/2 e n/2+1 dos dados ordenados.
![]()
![]()
Ouro
![]()
é o número total de itens de dados na amostra.
Exemplos de cálculo da mediana
Para que você possa ver como a mediana é calculada, abaixo estão dois exemplos do mundo real, um para cada caso. Primeiro, a mediana de um conjunto de dados ímpar será calculada e, em seguida, a mediana será calculada com um conjunto de dados par.
Mediana de dados ímpares
- Calcule a mediana dos seguintes dados: 3, 4, 1, 6, 7, 4, 8, 2, 8, 4, 5
A primeira coisa que precisamos fazer antes de realizar os cálculos é ordenar os dados, ou seja, colocamos os números do menor para o maior.
![]()
Neste caso temos 11 observações, então o número total de dados é ímpar. Portanto, aplicamos a seguinte fórmula para calcular a posição da mediana:
![]()
A mediana será, portanto, o dado localizado na sexta posição, que neste caso corresponde ao valor 4.
![]()
mediana de dados pares
- Qual é a mediana das seguintes observações? 2, 6, 2, 8, 9, 4, 7, 11, 4, 13
Para obter a mediana, primeiro você deve ordenar todos os dados em ordem crescente:
![]()
Este exemplo é diferente do anterior, pois desta vez temos um total de 10 observações, o que é um número par. Portanto, o procedimento para determinação da média é um pouco mais complicado.
Você deve primeiro calcular as duas posições centrais entre as quais a mediana será encontrada, para isso você deve aplicar as duas fórmulas a seguir:
![]()
![]()
A mediana estará portanto entre a quinta e a sexta posições, o que corresponde respectivamente aos valores 6 e 7. Concretamente, a mediana será a média aritmética dos referidos valores:
![]()
calculadora mediana
Insira um conjunto de dados estatísticos na calculadora a seguir para calcular sua mediana. Os dados devem ser separados por espaço e inseridos usando o ponto final como separador decimal.
Mediana para dados agrupados
Para calcular a mediana quando os dados são agrupados em intervalos, você deve primeiro encontrar o intervalo ou compartimento no qual a mediana se enquadra usando a seguinte fórmula:
![]()
Assim, a mediana estará no intervalo cuja frequência absoluta acumulada é imediatamente maior que o número obtido com a expressão algébrica anterior.
E uma vez conhecido o intervalo ao qual pertence a mediana, devemos aplicar a seguinte fórmula para encontrar o valor exato da mediana:

Ouro:
- L i é o limite inferior do intervalo em que se encontra a mediana.
- n é o número total de observações.
- F i-1 é a frequência absoluta acumulada do intervalo anterior.
- f i é a frequência absoluta do intervalo em que se encontra a mediana.
- I i é a largura do intervalo intermediário.
A título de exemplo, a seguir você resolveu um exercício no qual é calculada a mediana dos dados agrupados em intervalos.

Para encontrar a mediana do conjunto de dados, primeiro precisamos determinar o intervalo em que ela se enquadra. Para fazer isso, usamos a seguinte fórmula:
![]()
Então a mediana estará no intervalo cuja frequência absoluta acumulada é imediatamente maior que 15,5, que neste caso é o intervalo [60,70) cuja frequência absoluta acumulada é 26. E uma vez conhecido o intervalo mediano, aplicamos a segunda fórmula do processo:


Em última análise, a mediana do conjunto de dados agrupados é 60,45. Como você pode ver, nesses tipos de problemas a mediana geralmente é um número decimal.
mediana, média e moda
Nesta última seção veremos qual é a diferença entre a mediana, a média e a moda. Bem, estas são três medidas estatísticas de posição central, mas o seu significado é diferente.
Como vimos, a mediana é definida como o valor que ocupa a posição central quando os dados são ordenados.
Em contraste, a média é o valor médio de todos os dados estatísticos. Para calcular a média, você deve somar todos os dados e depois dividir o resultado pelo número de pontos de dados.
Finalmente, a moda é o valor mais repetido em uma série de dados.
Como você pode ver, todas as três medidas estatísticas ajudam a descrever uma distribuição de probabilidade, pois fornecem uma ideia de seus valores centrais. Porém, nenhuma medida é melhor que outra, elas simplesmente se referem a conceitos diferentes.