Como realizar regressão polinomial em python

A análise de regressão é usada para quantificar a relação entre uma ou mais variáveis explicativas e uma variável de resposta.

O tipo mais comum de análise de regressão é a regressão linear simples , usada quando uma variável preditora e uma variável resposta possuem um relacionamento linear.

No entanto, às vezes a relação entre uma variável preditora e uma variável de resposta é não linear.

Por exemplo, o relacionamento verdadeiro pode ser quadrático:

Ou pode ser cúbico:

Nestes casos, faz sentido utilizar a regressão polinomial , que pode dar conta da relação não linear entre as variáveis.

Este tutorial explica como realizar regressão polinomial em Python.

Exemplo: regressão polinomial em Python

Suponha que temos a seguinte variável preditora (x) e variável de resposta (y) em Python:

 x = [2, 3, 4, 5, 6, 7, 7, 8, 9, 11, 12]
y = [18, 16, 15, 17, 20, 23, 25, 28, 31, 30, 29]

Se criarmos um gráfico de dispersão simples desses dados, podemos ver que a relação entre x e y claramente não é linear:

 import matplotlib.pyplot as plt

#create scatterplot 
plt.scatter(x, y)

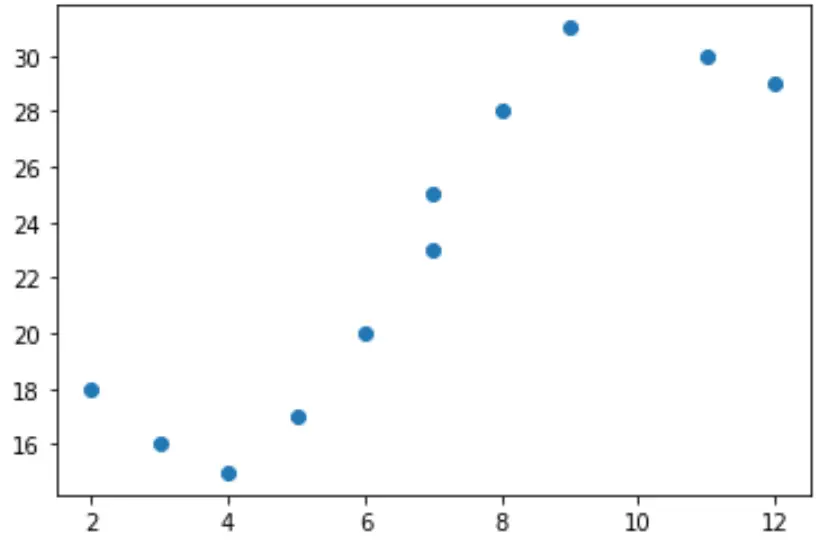
Portanto, não faria sentido ajustar um modelo de regressão linear a estes dados. Em vez disso, podemos tentar ajustar um modelo de regressão polinomial com grau 3 usando a função numpy.polyfit() :

 import numpy as np

#polynomial fit with degree = 3
model = np.poly1d(np.polyfit(x, y, 3))

#add fitted polynomial line to scatterplot
polyline = np.linspace(1, 12, 50)
plt.scatter(x, y)
plt.plot(polyline, model(polyline))
plt.show() 

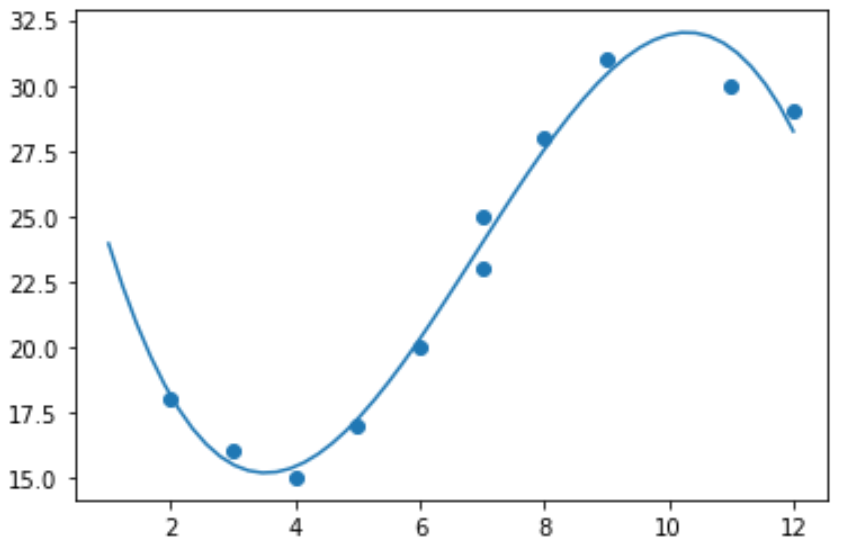
Podemos obter a equação de regressão polinomial ajustada imprimindo os coeficientes do modelo:

 print(model)

poly1d([ -0.10889554, 2.25592957, -11.83877127, 33.62640038])

A equação de regressão polinomial ajustada é:

y = -0,109x ³ + 2,256x ² – 11,839x + 33,626

Esta equação pode ser usada para encontrar o valor esperado da variável resposta dado um determinado valor da variável explicativa.

Por exemplo, suponha que x = 4. O valor esperado para a variável de resposta, y, seria:

y = -0,109(4) ³ + 2,256(4) ² – 11,839(4) + 33,626= 15,39 .

Também podemos escrever uma função curta para obter o R-quadrado do modelo, que é a proporção da variância na variável de resposta que pode ser explicada pelas variáveis preditoras.

 #define function to calculate r-squared
def polyfit(x, y, degree):
    results = {}
    coeffs = numpy.polyfit(x, y, degree)
    p = numpy.poly1d(coeffs)
    #calculate r-squared
    yhat = p(x)
    ybar = numpy.sum(y)/len(y)
    ssreg = numpy.sum((yhat-ybar)**2)
    sstot = numpy.sum((y - ybar)**2)
    results['r_squared'] = ssreg / sstot

    return results

#find r-squared of polynomial model with degree = 3
polyfit(x, y, 3)

{'r_squared': 0.9841113454245183}

Neste exemplo, o R quadrado do modelo é 0,9841 .

Isso significa que 98,41% da variação da variável resposta pode ser explicada pelas variáveis preditoras.