Como realizar um teste post hoc de tukey-kramer no excel
Uma ANOVA unidirecional é usada para determinar se há ou não uma diferença estatisticamente significativa entre as médias de três ou mais grupos independentes.
As suposições usadas em uma ANOVA são as seguintes:
A hipótese nula (H 0 ): µ 1 = µ 2 = µ 3 = … = µ k (as médias são iguais para cada grupo)
A hipótese alternativa: (Ha): pelo menos uma das médias é diferente das outras
Se o valor p da ANOVA estiver abaixo do nível de significância, podemos rejeitar a hipótese nula e concluir que temos evidências suficientes para dizer que pelo menos uma das médias do grupo é diferente das demais.
No entanto, isso não nos diz quais grupos são diferentes uns dos outros. Isto simplesmente nos diz que nem todas as médias dos grupos são iguais. Para saber exatamente quais grupos são diferentes entre si, precisamos realizar um teste post hoc.
O teste post hoc mais comumente usado é o teste de Tukey-Kramer , que compara a média entre cada combinação de grupos aos pares.
O exemplo a seguir mostra como realizar o teste Tukey-Kramer no Excel.
Exemplo: teste Tukey-Kramer no Excel
Suponha que realizamos uma ANOVA unidirecional em três grupos: A, B e C. Os resultados da ANOVA unidirecional são mostrados abaixo:
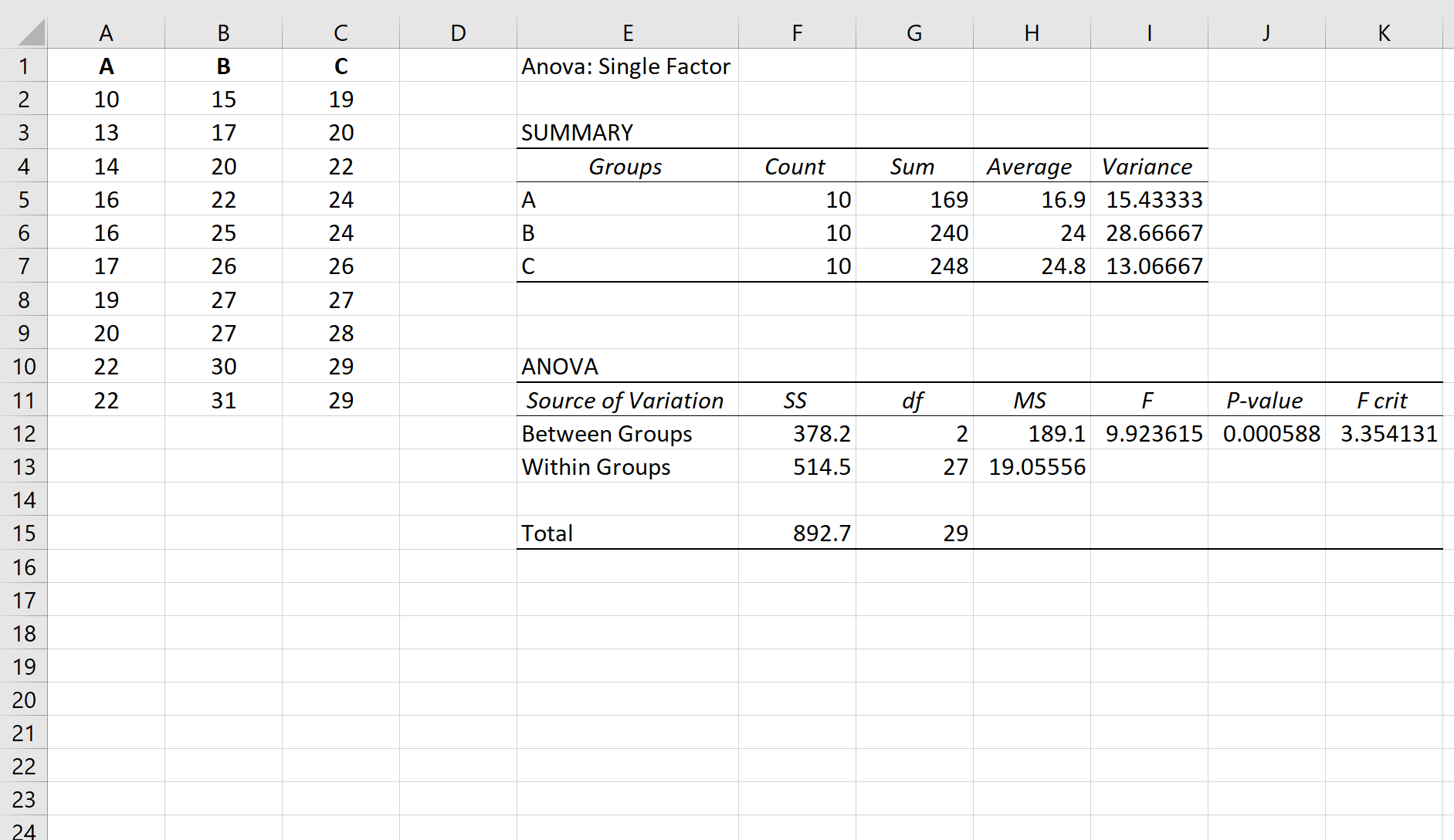
Relacionado: Como realizar ANOVA unidirecional no Excel
O valor p da tabela ANOVA é 0,000588 . Como este valor p é inferior a 0,05, podemos rejeitar a hipótese nula e concluir que as médias entre os três grupos não são iguais.
Para determinar exatamente quais médias de grupo são diferentes, podemos realizar um teste post hoc de Tukey-Kramer usando as seguintes etapas:
Etapa 1: Encontre a diferença média absoluta entre cada grupo.
Primeiro, encontraremos a diferença média absoluta entre cada grupo utilizando as médias listadas na primeira tabela do resultado da ANOVA:
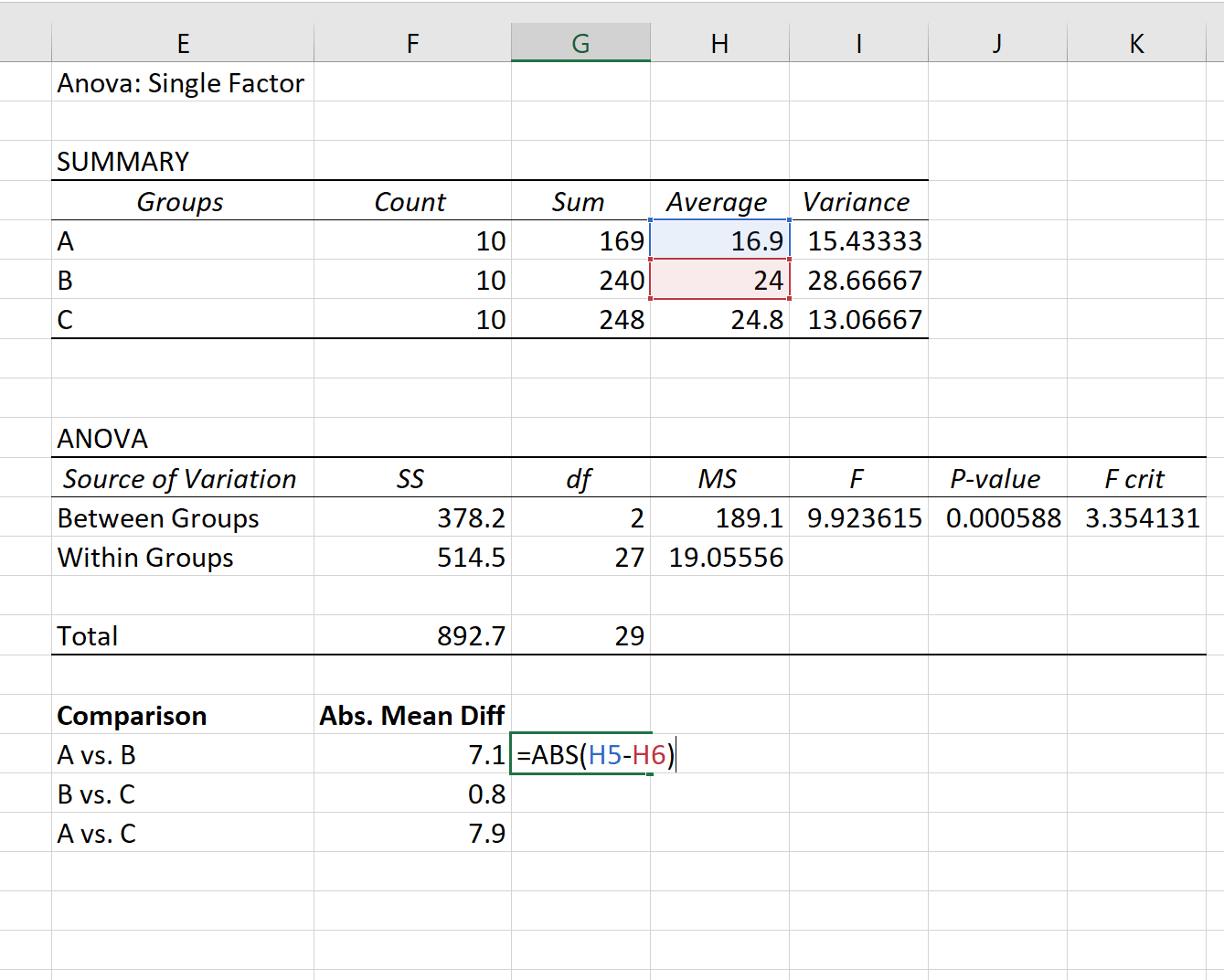
Etapa 2: Encontre o valor crítico de Q.
A seguir, precisamos encontrar o valor crítico de Q usando a seguinte fórmula:
Valor crítico Q = Q*√(s 2 agrupados / n.)
Ouro:
- Q = Valor do intervalo da Tabela Aluno Q
- s 2 agrupados = variância agrupada em todos os grupos
- não. = Tamanho da amostra para um determinado grupo
Para encontrar o valor Q, você pode consultar a tabela Q do intervalo estudantil, que se parece com isto:
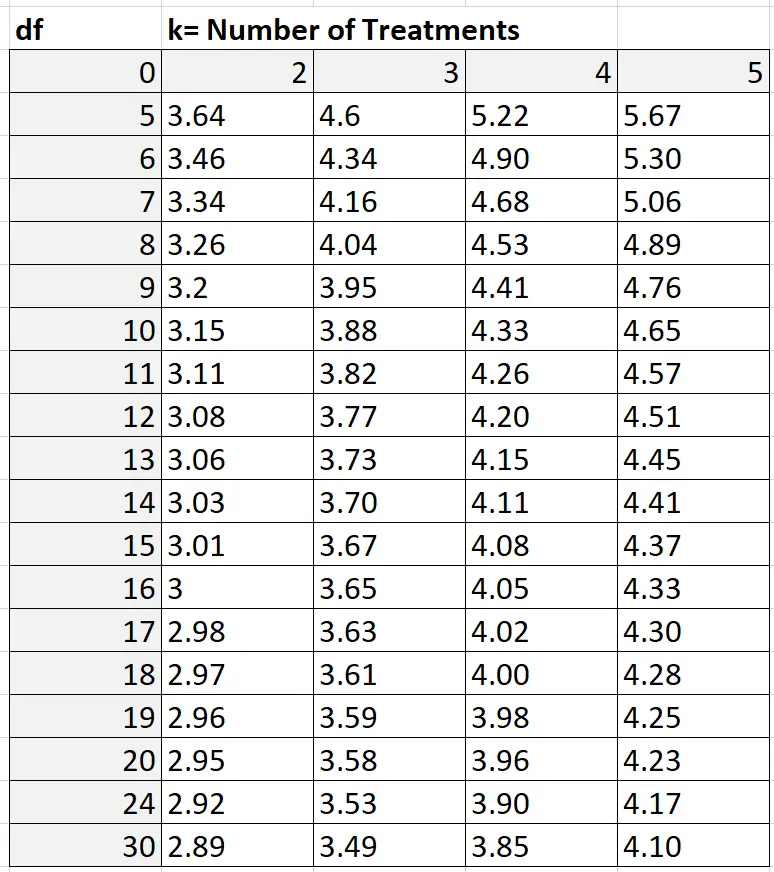
No nosso exemplo, k = o número de grupos, ou seja, k = 3. Os graus de liberdade são calculados como: nk = 30 – 3 = 27. Como 27 não é mostrado na tabela acima, podemos usar uma estimativa conservadora de 24 .Com base em k = 3 e df = 24, descobrimos que Q = 3,53 .
A variância agrupada pode ser calculada como a média das variâncias dos grupos, que resulta em 19,056 .
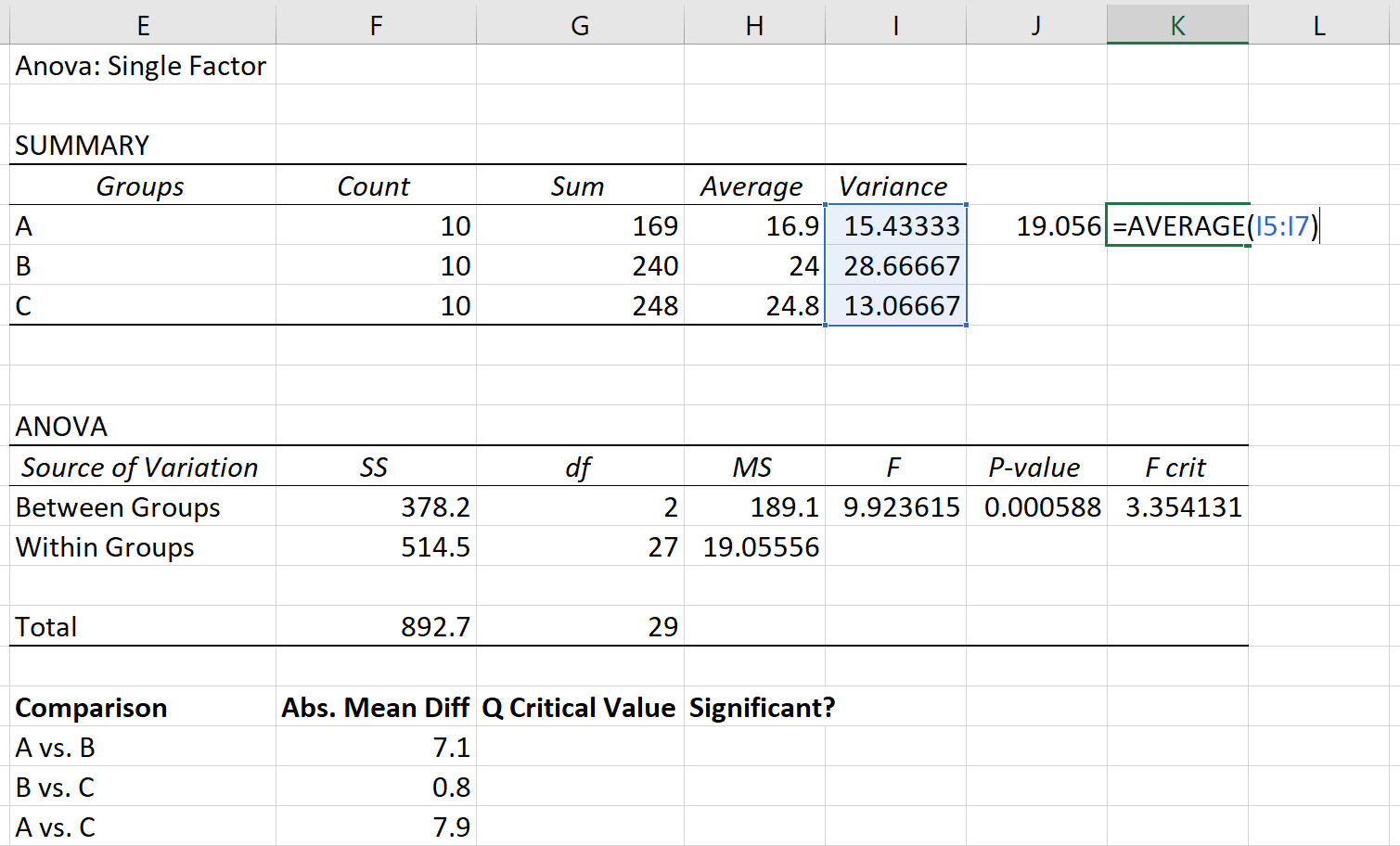
Finalmente, o tamanho da amostra de cada grupo é 10.
Assim, nosso valor crítico Q pode ser calculado da seguinte forma:
Valor crítico Q = Q*√(s 2 agrupados / n.) = 3,53*√(19,056/10) = 4,87 .
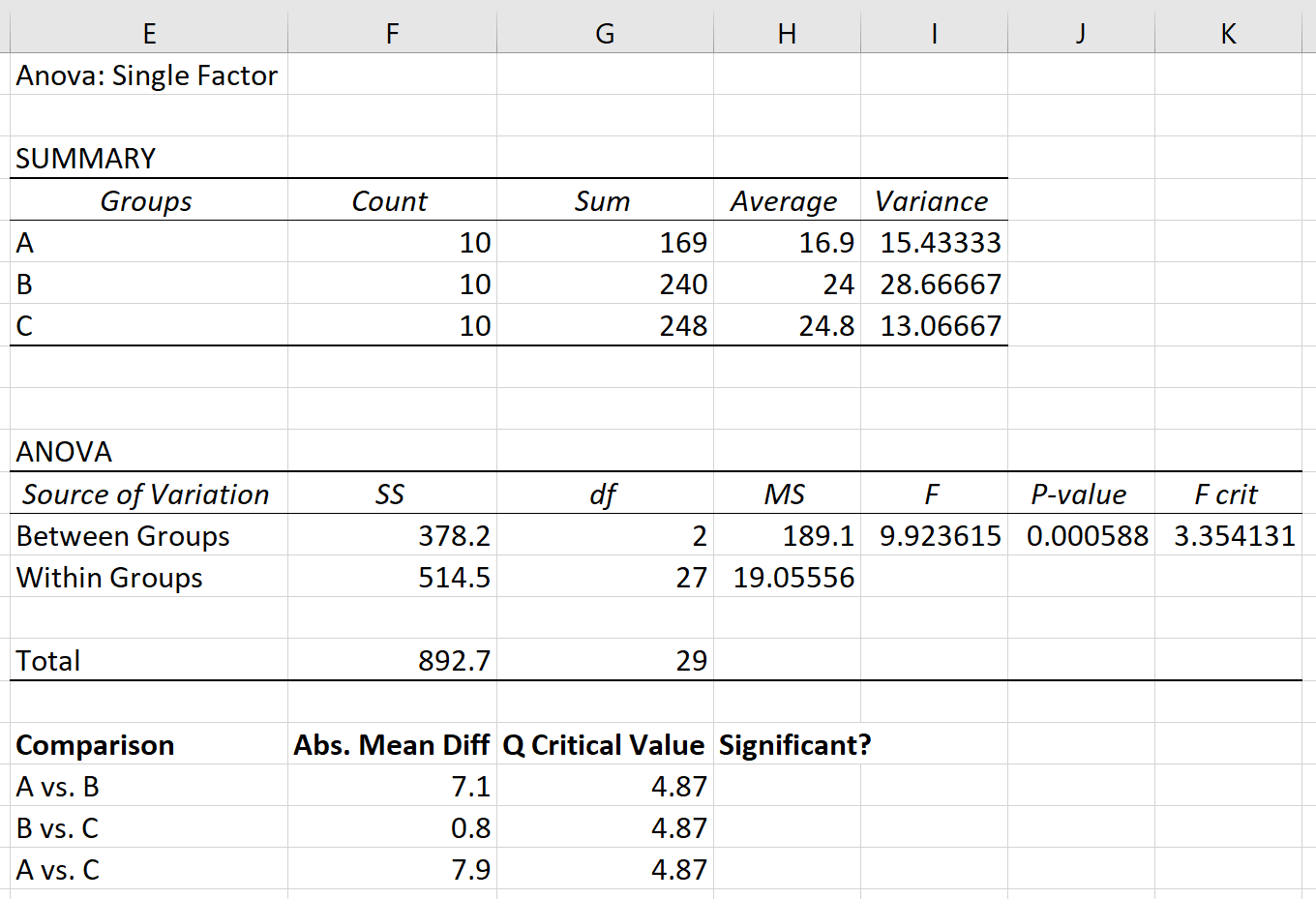
Etapa 3: Determine quais médias de grupo são diferentes .
Finalmente, podemos comparar a diferença média absoluta entre cada grupo com o valor crítico Q. Se a diferença média absoluta for maior que o valor crítico Q, então a diferença entre as médias do grupo é estatisticamente significativa:
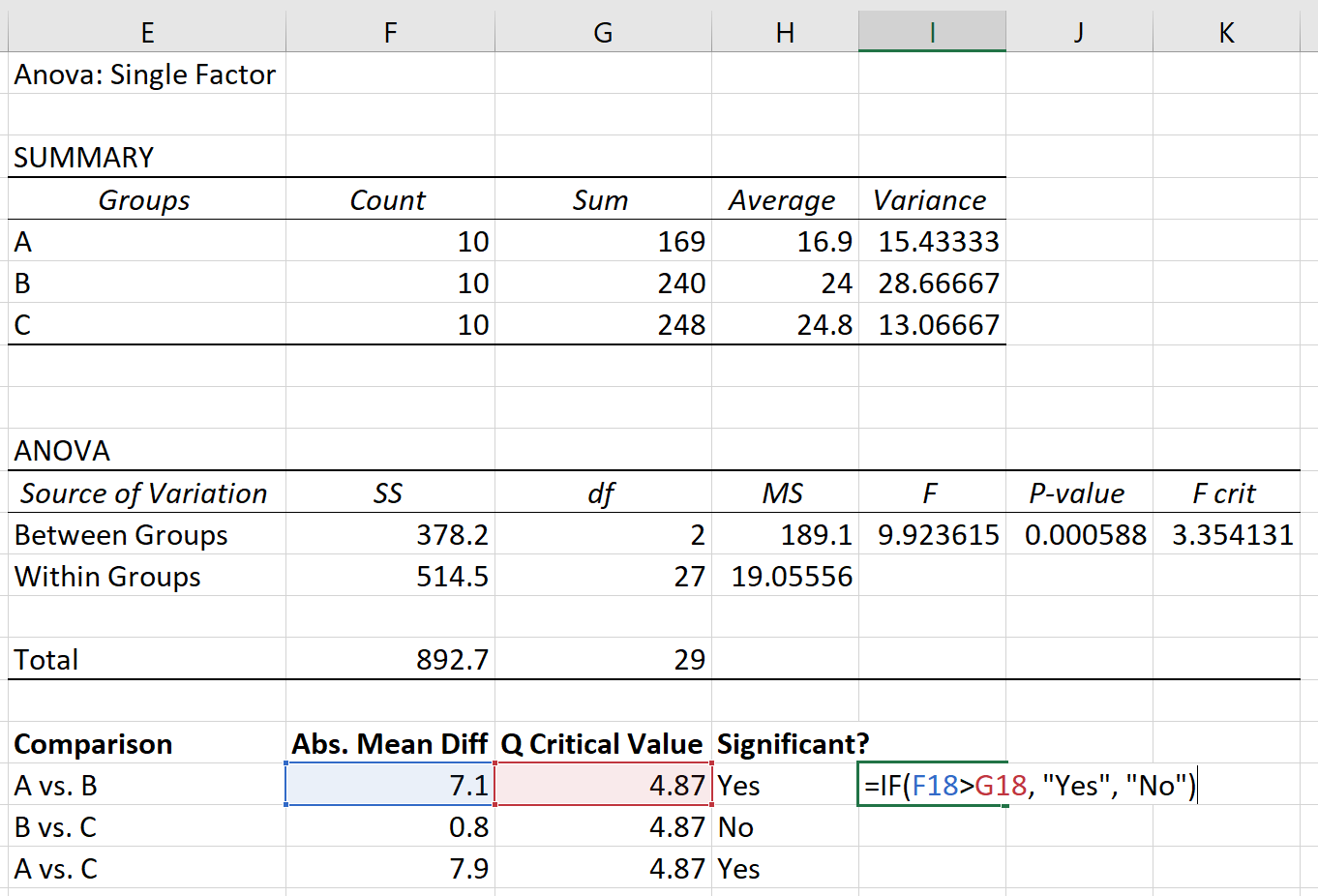
Com base no teste post hoc de Tukey-Kramer, encontramos o seguinte:
- A diferença de médias entre o grupo A e o grupo B é estatisticamente significativa.
- A diferença de médias entre o grupo B e o grupo C não é estatisticamente significativa.
- A diferença de médias entre o grupo A e o grupo C é estatisticamente significativa.
Recursos adicionais
Como realizar ANOVA unidirecional no Excel
Um guia para usar testes post-hoc com ANOVA