Moda (estatísticas)
Este artigo explica qual é o modo nas estatísticas. Você aprenderá como encontrar o modo estatístico para dados agrupados e dados desagrupados, os diferentes tipos de modo e vários exemplos desta medida estatística.
O que é modo nas estatísticas?
Nas estatísticas, a moda é o valor no conjunto de dados que possui a maior frequência absoluta, ou seja, a moda é o valor mais repetido em um conjunto de dados.
Portanto, para calcular a moda de um conjunto de dados estatísticos, basta contar o número de vezes que cada elemento de dados aparece na amostra, e os dados mais repetidos serão a moda.
A moda é usada para definir uma distribuição estatística, pois o valor mais repetido geralmente está no centro da distribuição.
O modo também pode ser considerado modo estatístico ou valor modal . Da mesma forma, quando os dados são agrupados em intervalos, o intervalo mais repetido é o intervalo modal ou classe modal .
Em geral, o termo Mo é usado como símbolo para o modo estatístico, por exemplo, o modo de distribuição X é Mo(X).
Tenha em mente que a moda é uma medida estatística da posição central, bem como da mediana e da média. A seguir veremos o que significa cada uma dessas medidas estatísticas.
Tipos de modo em estatísticas
Nas estatísticas, existem vários tipos de modos que são classificados de acordo com o número de valores mais repetidos:
- Modo Unimodal : existe apenas um valor com o número máximo de repetições. Por exemplo, [1, 4, 2, 4, 5, 3].
- Modo bimodal : O número máximo de repetições ocorre em dois valores diferentes, e ambos os valores são repetidos o mesmo número de vezes. Por exemplo, [2, 6, 7, 2, 3, 6, 9].
- Modo multimodal : Três ou mais valores possuem o mesmo número máximo de repetições. Por exemplo, [3, 3, 4, 1, 3, 4, 2, 1, 4, 5, 2, 1].
Como encontrar o modo estatístico
Para encontrar o modo estatístico de um conjunto de dados, você deve seguir as seguintes etapas:
- Coloque os dados em ordem. Esta etapa não é obrigatória, mas facilitará a contagem dos números.
- Conte quantas vezes cada número aparece.
- O número que aparece com mais frequência é o modo estatístico.
Exemplos de modo estatístico
Considerando a definição de moda nas estatísticas, abaixo você confere um exemplo de cada tipo de moda para que você possa entender melhor o conceito.
Exemplo de modo unimodal
- Qual é a moda do seguinte conjunto de dados?
![]()
Os números não estão ordenados, então vamos ordená-los primeiro para facilitar a localização da moda.
![]()
Os números 2 e 9 aparecem duas vezes, mas o número 5 se repete três vezes. Portanto, a moda da série de dados é o número 5.
![]()
Exemplo de modo bimodal
- Calcule a moda do seguinte conjunto de dados:
![]()
![]()
Primeiro colocamos os números em ordem:
![]()
![]()
Como você pode ver, o número 6 e o número 8 aparecem quatro vezes no total, que é o número máximo de repetições. Portanto, neste caso é um modo bimodal e os dois números são a moda do conjunto de dados:
![]()
Exemplo de modo multimodal
- Encontre o seguinte modo de conjunto de dados:
![]()
![]()
![]()
Como há muitos dados, primeiro os classificamos em ordem crescente para facilitar a contagem:
![]()
![]()
![]()
Os números mais repetidos são 20, 27 e 31, todos os três números são repetidos cinco vezes. O modo deste exemplo é, portanto, multimodal.
![]()
calculadora de moda
Insira dados de qualquer amostra estatística na calculadora on-line a seguir para calcular sua moda. Os dados devem ser separados por espaço e inseridos usando o ponto final como separador decimal.
Modo para dados agrupados
Quando temos dados agrupados na forma de intervalos, não sabemos realmente quantas vezes cada dado se repete, apenas sabemos a frequência de cada intervalo.
Assim, para calcular a moda dos dados agrupados em intervalos, devemos utilizar a seguinte fórmula :
![]()
Ouro:
- L i é o limite inferior do intervalo modal (maior intervalo de frequência absoluta).
- f i é a frequência absoluta do intervalo modal.
- f i-1 é a frequência absoluta do intervalo antes do modal.
- f i+1 é a frequência absoluta do intervalo após o modal.
- A i é a largura do intervalo modal.
A título de exemplo, a seguir você resolveu um exercício no qual é calculada a moda dos dados agrupados em intervalos:
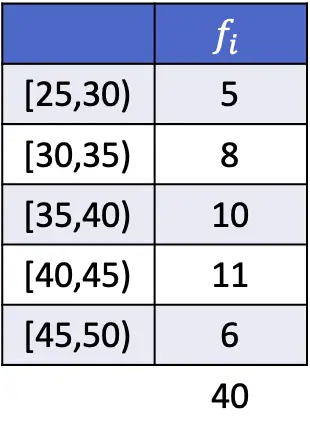
Neste caso, o intervalo modal é [40,45), pois é o intervalo com maior frequência absoluta. Portanto, os parâmetros da fórmula de modo para dados agrupados são:
![Rendered by QuickLaTeX.com \begin{array}{c}L_i=40\\[2ex]f_i=11\\[2ex]f_{i-1}=10\\[2ex]f_{i+1}=6\\[2ex]A_i=5\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-85aef7092d3e0c7769ad17b96aae294c_l3.png)
Portanto, aplicamos a fórmula para determinar a moda dos dados agrupados em intervalos e fazemos o cálculo:
![Rendered by QuickLaTeX.com \begin{aligned}Mo & =L_i+ \cfrac{f_i-f_{i-1}}{(f_i-f_{i-1})+(f_i-f_{i+1})}\cdot A_i\\[2ex]& =40+ \cfrac{11-10}{(11-10)+(11-6)}\cdot 5\\[2ex]&=40,83\end{aligned}](https://statorials.org/wp-content/ql-cache/quicklatex.com-3ee33fdb43267fdcfc6d222ed6798fca_l3.png)
Diferença entre moda, média e mediana
Nesta última seção veremos qual é a diferença entre a moda, a média e a mediana. Dado que todos os três são medidas estatísticas de posição central, o seu significado é diferente.
Conforme explicado ao longo do artigo, a moda em matemática é o valor mais repetido em um conjunto de dados.
Em segundo lugar, a média é o valor médio de todos os dados estatísticos. Assim, para obter a média de determinados dados, deve-se somar todos os dados e depois dividir o resultado pelo número de observações.
E por fim, a mediana é o valor que ocupa a posição central quando os dados são ordenados.
Assim, as três medidas estatísticas ajudam a definir uma distribuição de probabilidade, pois dão uma ideia dos seus valores centrais. Mas lembre-se de que não existe uma medida melhor que outra, apenas significam conceitos diferentes.
Propriedades da moda
As propriedades da moda são:
- A moda pode ser encontrada tanto em variáveis quantitativas quanto em variáveis qualitativas.
- Se aplicarmos uma transformação linear a uma variável aleatória, o valor da média mudará dependendo das operações aplicadas.
- Em geral, o modo é insensível a valores discrepantes.
- Se todos os valores tiverem a mesma frequência, não existe moda.
![]()