Como calcular o erro padrão da média no excel

O erro padrão da média é uma forma de medir a distribuição de valores em um conjunto de dados. É calculado da seguinte forma:

Erro padrão = s / √n

Ouro:

• s : desvio padrão da amostra
• n : tamanho da amostra

Você pode calcular o erro padrão da média de qualquer conjunto de dados no Excel usando a seguinte fórmula:

= STDEV (intervalo de valores) / SQRT ( COUNT (intervalo de valores))

O exemplo a seguir mostra como usar esta fórmula.

Exemplo: erro padrão no Excel

Suponha que temos o seguinte conjunto de dados:

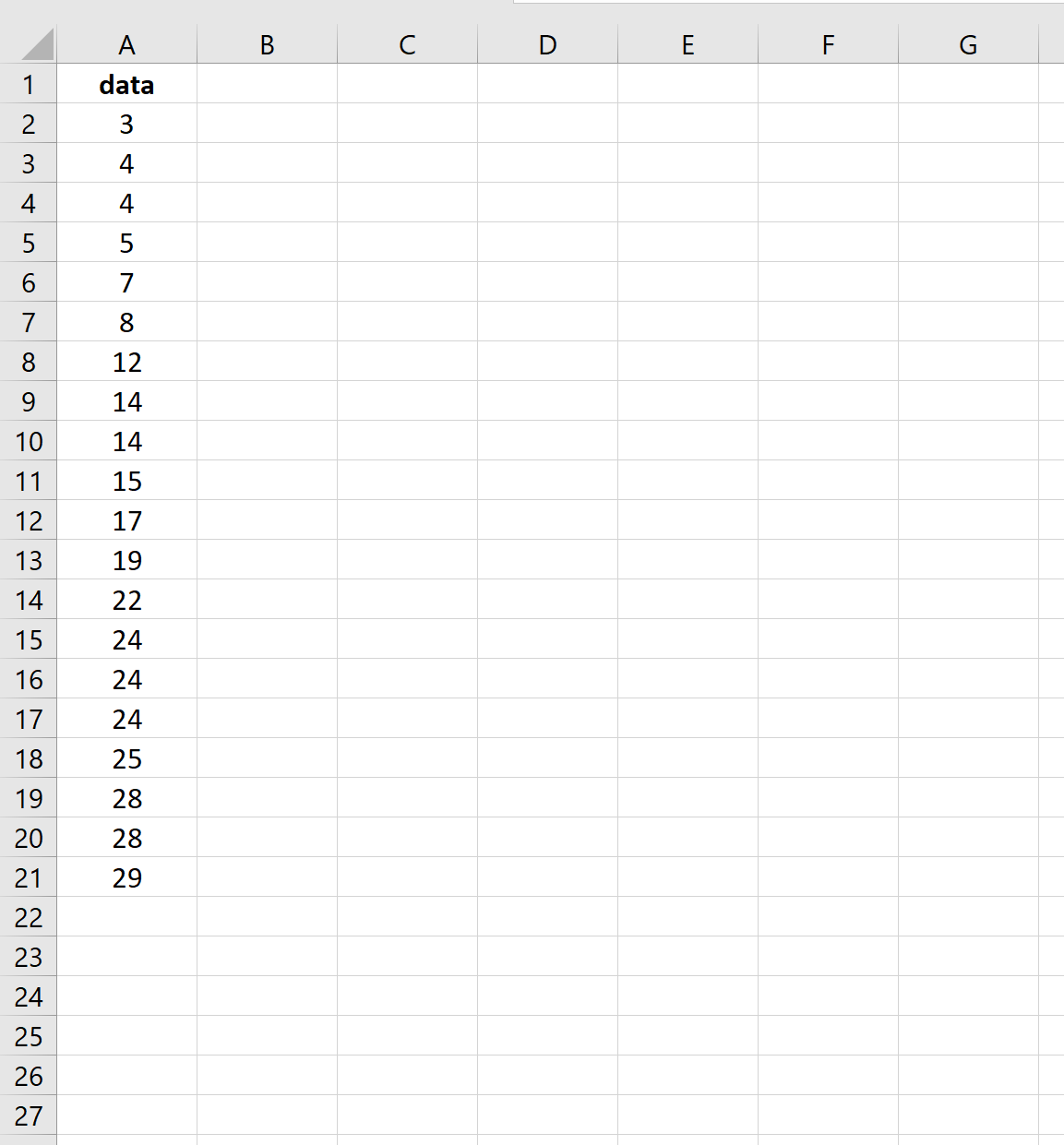
A captura de tela a seguir mostra como calcular o erro padrão da média para este conjunto de dados:

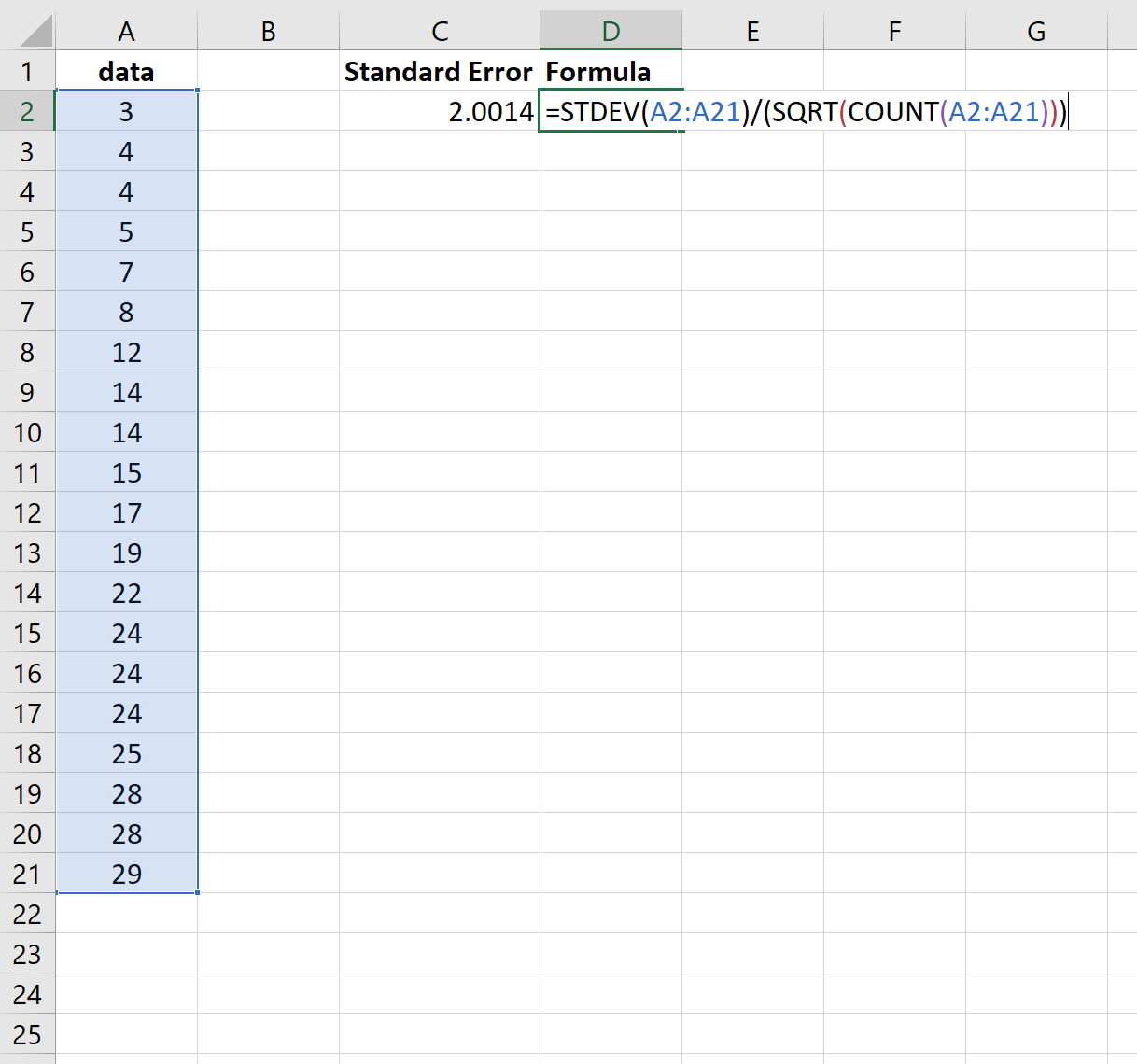
O erro padrão é 2.0014 .

Observe que a função =STDEV() calcula a média amostral, que é equivalente à função =STDEV.S() no Excel.

Então, poderíamos ter usado a seguinte fórmula para obter os mesmos resultados:

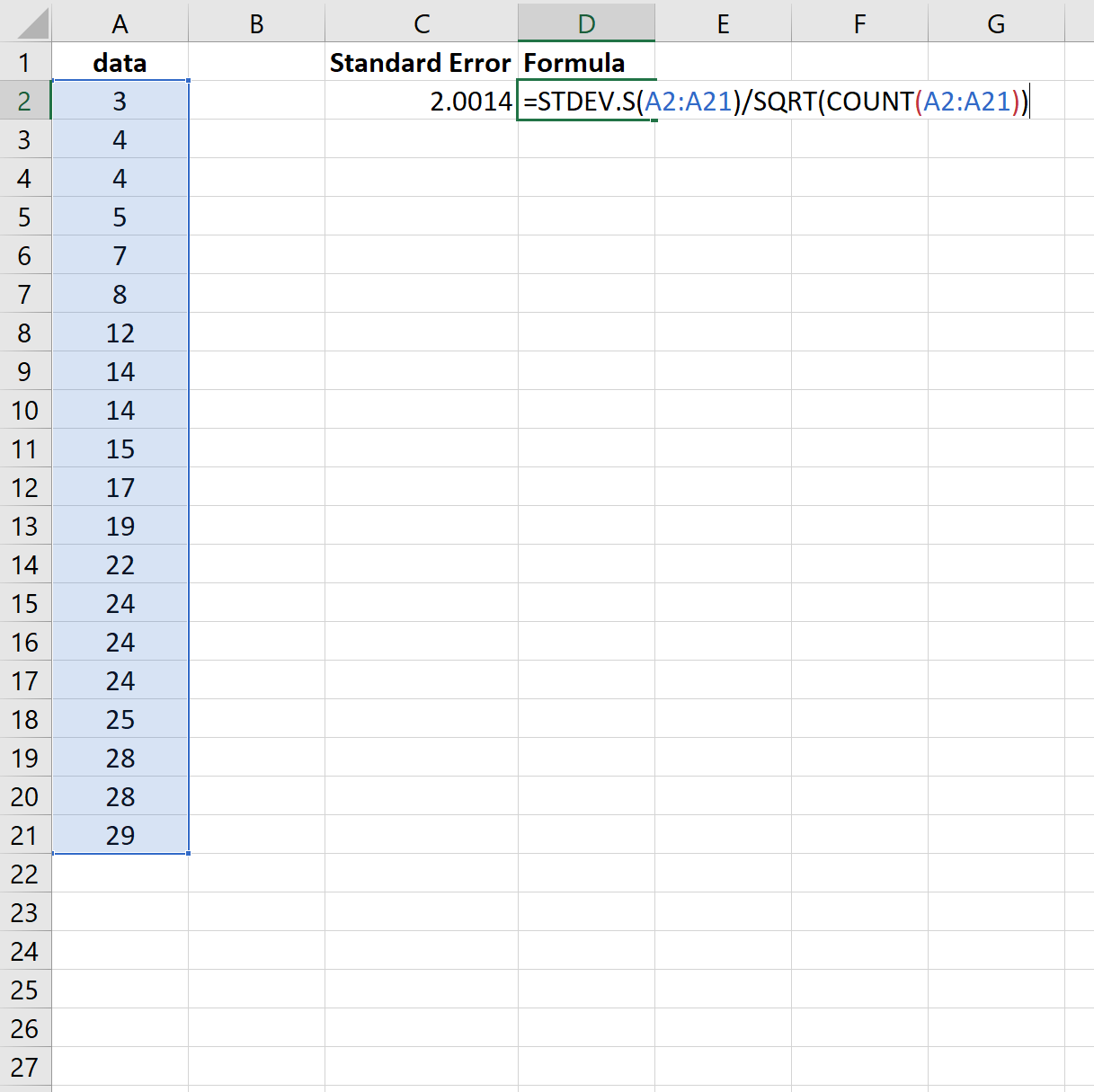
Mais uma vez, o erro padrão é 2,0014 .

Como interpretar o erro padrão da média

O erro padrão da média é simplesmente uma medida da dispersão dos valores em torno da média. Há duas coisas a se ter em mente ao interpretar o erro padrão da média:

1. Quanto maior o erro padrão da média, mais dispersos estão os valores em torno da média em um conjunto de dados.

Para ilustrar isso, considere se alterarmos o último valor do conjunto de dados anterior por um número muito maior:

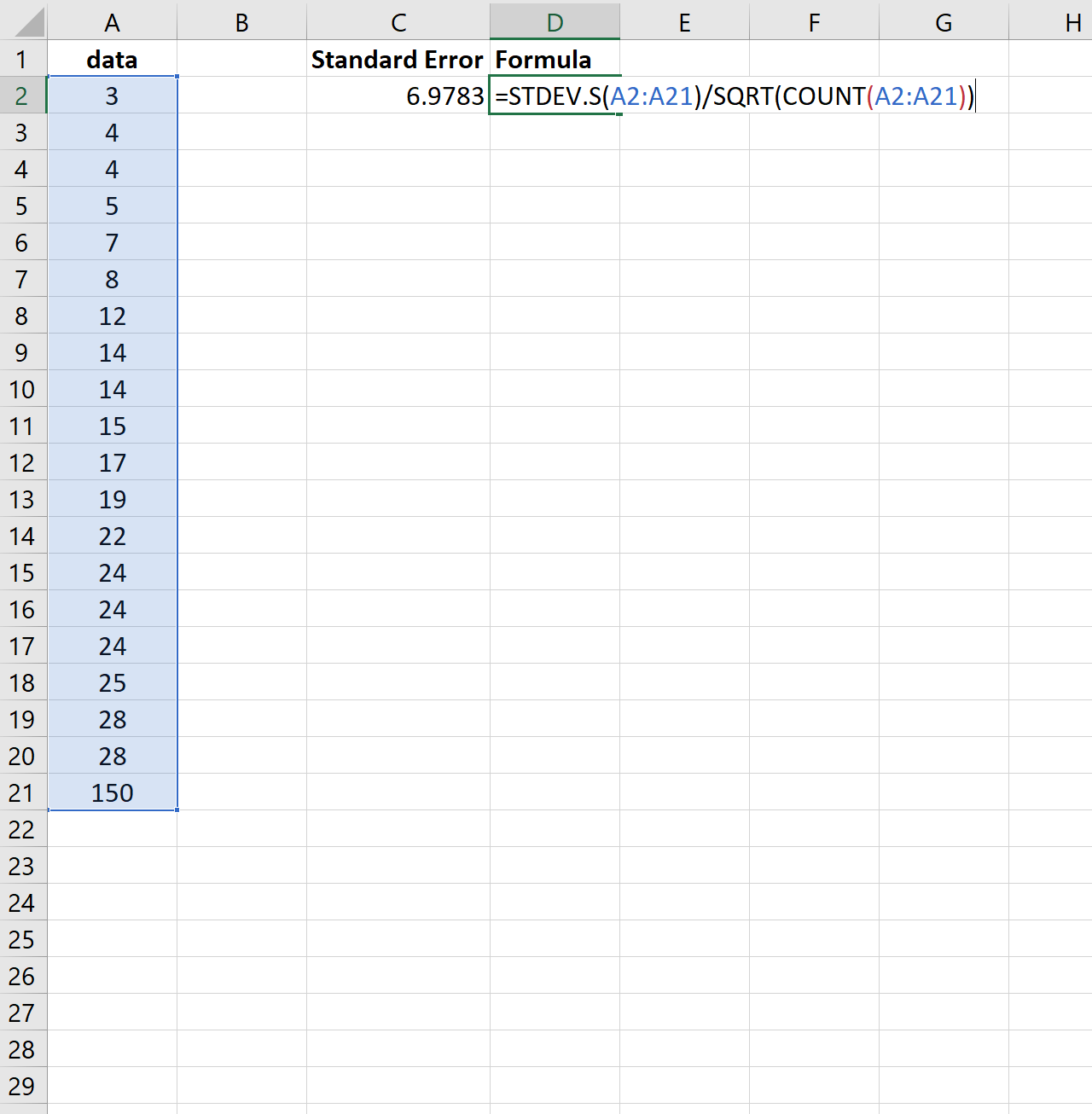
Observe como o erro padrão aumenta de 2,0014 para 6,9783 . Isso indica que os valores neste conjunto de dados estão mais distribuídos em torno da média em comparação com o conjunto de dados anterior.

2. À medida que o tamanho da amostra aumenta, o erro padrão da média tende a diminuir.

Para ilustrar isso, considere o erro padrão da média para os dois conjuntos de dados a seguir:

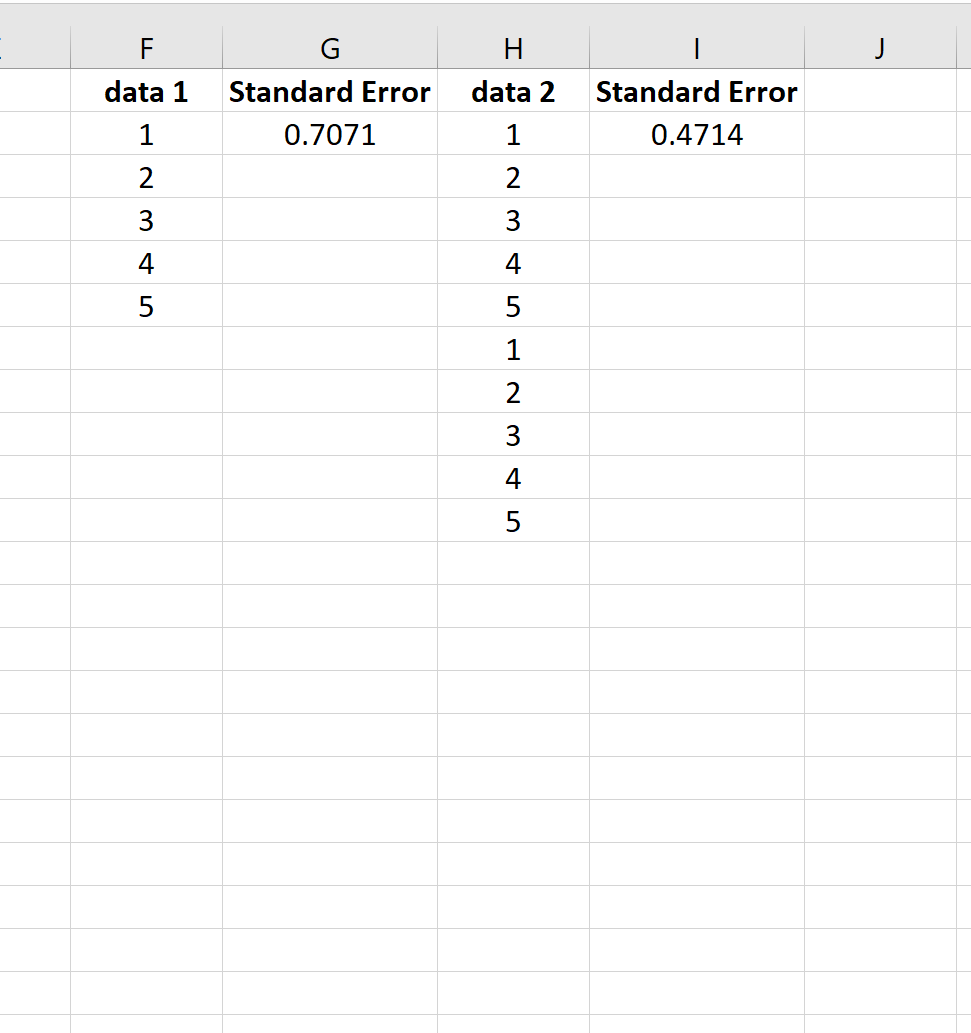
O segundo conjunto de dados é simplesmente o primeiro conjunto de dados repetido duas vezes. Portanto, ambos os conjuntos de dados têm a mesma média, mas o segundo conjunto de dados tem um tamanho de amostra maior e, portanto, tem um erro padrão menor.