Média, mediana e moda

By Agosto 5, 2023 Estatisticas 0 Comments

Este artigo explica o que são média, mediana e moda. Você aprenderá como obter a média, a mediana e a moda, para que são usadas e qual é a diferença entre essas três medidas estatísticas. Além disso, você poderá calcular a média, mediana e moda de qualquer amostra estatística com a calculadora online no final.

Qual é a média, mediana e moda?

A média, mediana e moda são medidas estatísticas de posição central. Ou seja, a média, a mediana e a moda são valores que ajudam a definir uma amostra estatística, nomeadamente, indicam quais são os seus valores centrais.

A média, mediana e moda são definidas da seguinte forma:

  • Média : é a média de todos os dados da amostra.
  • Mediana : Este é o valor médio de todos os dados ordenados do menor para o maior.
  • Moda : Este é o valor mais repetido no conjunto de dados.

Estas três medidas estatísticas são explicadas mais detalhadamente abaixo.

Metade

Para calcular a média, some todos os valores e depois divida pelo número total de dados. A fórmula para a média é, portanto, a seguinte:

\displaystyle\overline{x}=\frac{\displaystyle\sum_{i=1}^N x_i}{N}

👉 Você pode usar a calculadora abaixo para calcular a média, mediana e moda de qualquer conjunto de dados.

O símbolo médio é uma faixa horizontal acima da letra x

(\overline{x}).

Você também pode diferenciar a média amostral da média populacional com o símbolo de média: a média de uma amostra é expressa com o símbolo

\overline{x}

, enquanto a média de uma população usa a letra grega

\mu.

A média também é conhecida como média aritmética ou média . Além disso, a média de uma distribuição estatística é equivalente à sua expectativa matemática.

Exemplo médio

  • Um aluno obteve as seguintes notas durante um ano letivo: em matemática 9, em línguas 7, em história 6, em economia 8 e em ciências 7,5. Qual é a média de todas as suas notas?

Para encontrar a média aritmética, precisamos somar todas as notas e depois dividir pelo total de disciplinas do curso, que é 5. Portanto, aplicamos a fórmula da média aritmética:

\displaystyle\overline{x}=\frac{\displaystyle\sum_{i=1}^N x_i}{N}

Substituímos os dados na fórmula e calculamos a média aritmética:

\overline{x}=\cfrac{9+7+5+8+7,5}{5}=7,3

Como você pode ver, na média aritmética é atribuído o mesmo peso a cada valor, ou seja, cada dado tem o mesmo peso dentro do todo.

Mediana

A mediana é o valor médio de todos os dados ordenados do menor para o maior. Em outras palavras, a mediana divide o conjunto de dados ordenado em duas partes iguais.

O cálculo da mediana depende se o número total de dados é par ou ímpar:

  • Se o número total de dados for ímpar , a mediana será o valor que fica bem no meio dos dados. Ou seja, o valor que está na posição (n+1)/2 dos dados ordenados.

    • Me=x_{\frac{n+1}{2}

  • Se o número total de pontos de dados for par , a mediana será a média dos dois pontos de dados localizados no centro. Ou seja, a média aritmética dos valores que se encontram nas posições n/2 e n/2+1 dos dados ordenados.

    • Me=\cfrac{x_{\frac{n}{2}}+x_{\frac{n}{2}+1}}{2}

Ouro

n

é o número total de itens de dados na amostra.

O termo Me é frequentemente usado como símbolo para indicar que um valor é a mediana de todas as observações.

👉 Você pode usar a calculadora abaixo para calcular a média, mediana e moda de qualquer conjunto de dados.

Exemplo mediano

  • Encontre a mediana dos seguintes dados: 3, 4, 1, 6, 7, 4, 8, 2, 8, 4, 5

A primeira coisa a fazer antes de fazer os cálculos é classificar os dados, ou seja, colocamos os números do menor para o maior.

1 \ 2 \ 3 \ 4 \ 4 \ 4 \ 5 \ 6 \ 7 \ 8 \ 8

Neste caso temos 11 observações, então o número total de dados é ímpar. Portanto, aplicamos a seguinte fórmula para calcular a posição da mediana:

\cfrac{n+1}{2}=\cfrac{11+1}{2}=6

A mediana será, portanto, o dado localizado na sexta posição, que neste caso corresponde ao valor 4.

Me=x_6=4

Moda

Nas estatísticas, a moda é o valor no conjunto de dados que possui a maior frequência absoluta, ou seja, a moda é o valor mais repetido em um conjunto de dados.

Portanto, para calcular a moda de um conjunto de dados estatísticos, basta contar o número de vezes que cada elemento de dado aparece na amostra, e os dados mais repetidos serão a moda.

O modo também pode ser considerado modo estatístico ou valor modal . Da mesma forma, quando os dados são agrupados em intervalos, o intervalo mais repetido é o intervalo modal ou classe modal .

Em geral, o termo Mo é usado como símbolo para o modo estatístico, por exemplo, o modo de distribuição X é Mo(X).

Três tipos de modos podem ser distinguidos de acordo com o número de valores mais repetidos:

  • Modo Unimodal : existe apenas um valor com o número máximo de repetições. Por exemplo, [1, 4, 2, 4, 5, 3].
  • Modo bimodal : O número máximo de repetições ocorre em dois valores diferentes, e ambos os valores são repetidos o mesmo número de vezes. Por exemplo, [2, 6, 7, 2, 3, 6, 9].
  • Modo multimodal : Três ou mais valores possuem o mesmo número máximo de repetições. Por exemplo, [3, 3, 4, 1, 3, 4, 2, 1, 4, 5, 2, 1].

👉 Você pode usar a calculadora abaixo para calcular a média, mediana e moda de qualquer conjunto de dados.

exemplo de moda

  • Qual é a moda do seguinte conjunto de dados?

5 \ 4 \ 9 \ 7 \ 2 \ 3 \ 9 \ 6 \ 5 \ 2 \ 5

Os números estão fora de ordem, então a primeira coisa que faremos é classificá-los. Essa etapa não é obrigatória, mas vai te ajudar a encontrar moda com mais facilidade.

2 \ 2 \ 3 \ 4 \ 5 \ 5 \ 5 \ 6 \ 7 \ 9 \ 9

Os números 2 e 9 aparecem duas vezes, mas o número 5 se repete três vezes. Portanto, a moda da série de dados é o número 5.

Mo=5

Exercício resolvido de média, mediana e moda

Agora que você sabe o que são média, mediana e moda, abaixo está um exercício elaborado sobre essas medidas estatísticas para que você possa ver exatamente como elas são calculadas.

  • Encontre a média, mediana e moda do seguinte conjunto de dados estatísticos:

8 \ 7 \ 0 \ 6 \ 10 \ 9 \ 13 \ 8 \ 0 \ 6 \ 2 \ 6 \ 5 \ 11 \ 10

0 \ 9 \ 8 \ 6 \ 12 \ 3 \ 5 \ 11 \ 1 \ 4 \ 8 \ 10 \ 2 \ 5 \ 7

Para encontrar a média dos dados, precisamos somar tudo e depois dividir pelo número total de dados, que é 30:

\displaystyle\overline{x}=\frac{\displaystyle\sum_{i=1}^N x_i}{N}=\frac{192}{30}=6,4

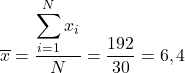
Em segundo lugar, vamos descobrir a mediana da amostra. Então colocamos todos os números em ordem crescente:

0 \ 0 \ 0 \ 1 \ 2 \ 2 \ 3 \ 4 \ 5 \ 5 \ 5 \ 6 \ 6 \ 6 \ 6

7 \ 7 \ 8 \ 8 \ 8 \ 8 \ 9 \ 9 \ 10 \ 10 \ 10 \ 11 \ 11 \ 12 \ 13

Neste caso, o número total de dados é par, por isso é necessário calcular as duas posições centrais entre as quais será encontrada a mediana. Para isso usamos as duas fórmulas a seguir:

\cfrac{n}{2}=\cfrac{30}{2}=15

\cfrac{n}{2}+1=\cfrac{30}{2}+1=16

A mediana estará portanto entre a décima quinta e a décima sexta posição, o que corresponde respetivamente aos valores 6 e 7. Mais precisamente, a mediana equivale à média destes valores:

Me=\cfrac{x_{15}+x_{16}}{2}=\cfrac{6+7}{2}=6,5

Por fim, para encontrar a moda basta contar todas as vezes que cada número aparece. Como você pode ver, o número 6 e o número 8 aparecem quatro vezes no total, que é o número máximo de repetições. Portanto, neste caso é um modo bimodal e os dois números são a moda do conjunto de dados:

Mo=\{ 6 \ ; \ 8\}

Calculadora de média, mediana e modo

Insira dados de qualquer amostra estatística na calculadora on-line a seguir para calcular sua média, mediana e moda. Os dados devem ser separados por espaço e inseridos usando o ponto final como separador decimal.

About Author

Dr. Benjamin Anderson
Dr. benjamim anderson

Olá, sou Benjamin, um professor aposentado de estatística que se tornou professor dedicado na Statorials. Com vasta experiência e conhecimento na área de estatística, estou empenhado em compartilhar meu conhecimento para capacitar os alunos por meio de Statorials. Saber mais

Add a Comment

O seu endereço de email não será publicado. Campos obrigatórios marcados com *