Como realizar regressão quadrática em python

A regressão quadrática é um tipo de regressão que podemos usar para quantificar a relação entre uma variável preditora e uma variável de resposta quando as verdadeiras relações são quadráticas, o que pode parecer um “U” ou um “U” invertido em um gráfico.

Ou seja, à medida que a variável preditora aumenta, a variável resposta tende a aumentar também, mas depois de um certo ponto a variável resposta começa a diminuir à medida que a variável preditora continua a aumentar.

Este tutorial explica como realizar regressão quadrática em Python.

Exemplo: regressão quadrática em Python

Suponha que temos dados sobre o número de horas trabalhadas por semana e o nível de felicidade relatado (numa escala de 0 a 100) para 16 pessoas diferentes:

 import numpy as np
import scipy.stats as stats

#define variables
hours = [6, 9, 12, 12, 15, 21, 24, 24, 27, 30, 36, 39, 45, 48, 57, 60]
happ = [12, 18, 30, 42, 48, 78, 90, 96, 96, 90, 84, 78, 66, 54, 36, 24]

Se fizermos um gráfico de dispersão simples desses dados, podemos ver que a relação entre as duas variáveis tem formato de “U”:

 import matplotlib.pyplot as plt

#create scatterplot
plt.scatter(hours, happ) 

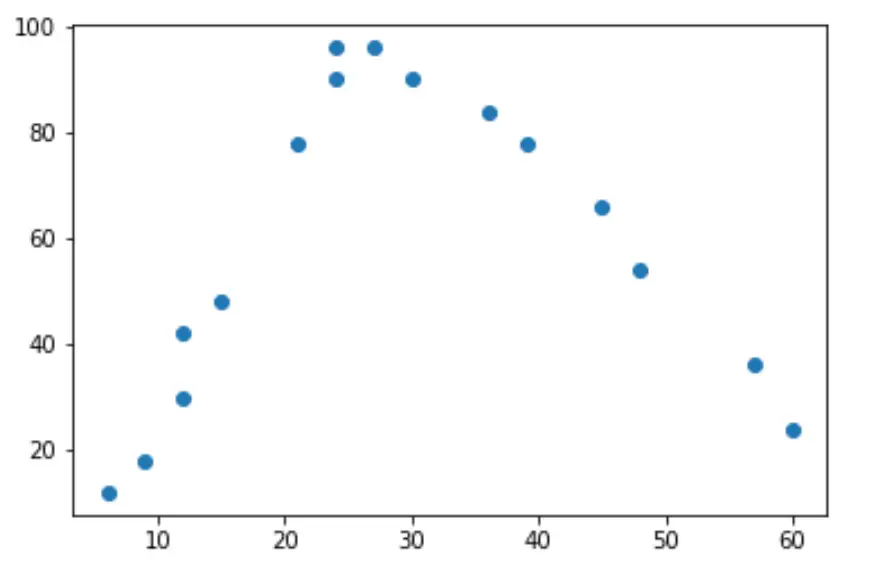
À medida que as horas trabalhadas aumentam, a felicidade também aumenta, mas quando as horas trabalhadas ultrapassam cerca de 35 horas por semana, a felicidade começa a diminuir.

Devido ao formato em “U”, isso significa que a regressão quadrática é provavelmente uma boa candidata para quantificar a relação entre as duas variáveis.

Para realmente realizar uma regressão quadrática, podemos ajustar um modelo de regressão polinomial com grau 2 usando a função numpy.polyfit() :

 import numpy as np

#polynomial fit with degree = 2
model = np.poly1d(np.polyfit(hours, happ, 2))

#add fitted polynomial line to scatterplot
polyline = np.linspace(1, 60, 50)
plt.scatter(hours, happ)
plt.plot(polyline, model(polyline))
plt.show() 

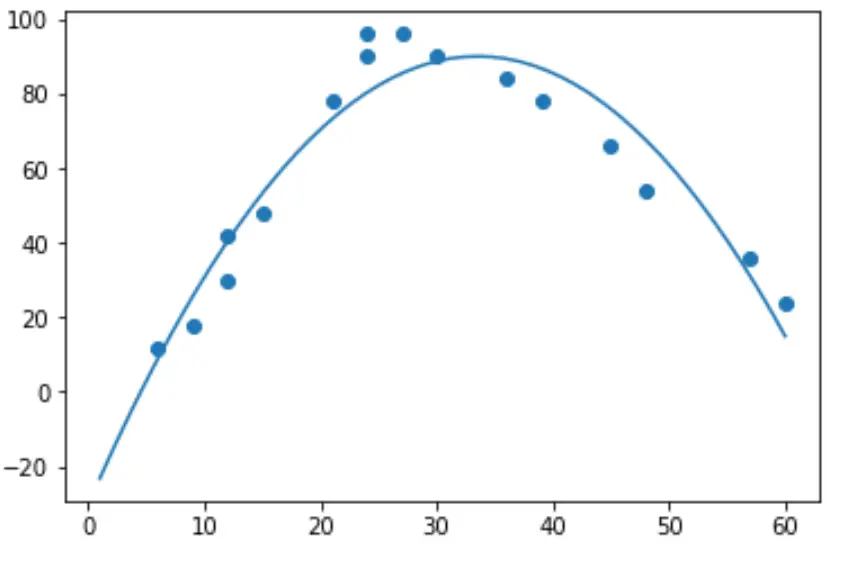
Podemos obter a equação de regressão polinomial ajustada imprimindo os coeficientes do modelo:

 print (model)

-0.107x 2 + 7.173x - 30.25

A equação de regressão quadrática ajustada é:

Felicidade = -0,107(horas) ² + 7,173(horas) – 30,25

Podemos usar esta equação para calcular o nível de felicidade esperado de um indivíduo com base nas horas trabalhadas. Por exemplo, o nível de felicidade esperado de uma pessoa que trabalha 30 horas por semana é:

Felicidade = -0,107(30) ² + 7,173(30) – 30,25 = 88,64 .

Também podemos escrever uma função curta para obter o R-quadrado do modelo, que é a proporção da variância na variável de resposta que pode ser explicada pelas variáveis preditoras.

 #define function to calculate r-squared
def polyfit(x, y, degree):
    results = {}
    coeffs = np.polyfit(x, y, degree)
    p = np.poly1d(coeffs)
    #calculate r-squared
    yhat = p(x)
    ybar = np.sum(y)/len(y)
    ssreg = np.sum((yhat-ybar)**2)
    sstot = np.sum((y - ybar)**2)
    results['r_squared'] = ssreg / sstot

    return results

#find r-squared of polynomial model with degree = 3
polyfit(hours, happ, 2)

{'r_squared': 0.9092114182131691}

Neste exemplo, o R quadrado do modelo é 0,9092 .

Isto significa que 90,92% da variação nos níveis de felicidade relatados pode ser explicada pelas variáveis preditoras.

Recursos adicionais

Como realizar regressão polinomial em Python
Como realizar regressão quadrática em R
Como realizar regressão quadrática no Excel