A distribuição normal
A distribuição normal é a distribuição de probabilidade mais comum nas estatísticas.
As distribuições normais têm as seguintes características:
- Formato de sino
- Simétrico
- A média e a mediana são iguais; ambos estão localizados no centro da distribuição
- Cerca de 68% dos dados estão dentro de um desvio padrão da média
- Cerca de 95% dos dados estão dentro de dois desvios padrão da média.
- Cerca de 99,7% dos dados estão dentro de três desvios padrão da média.
Os últimos três pontos são conhecidos como regra prática , às vezes chamada de regra 68-95-99,7 .
Relacionado: Regra prática (questões práticas)
Como desenhar uma curva normal
Para desenhar uma curva normal, precisamos saber a média e o desvio padrão.
Exemplo 1: Suponha que a altura dos homens em uma determinada escola seja normalmente distribuída com média de desvio padrão de
Etapa 1: esboce uma curva normal.
Passo 2: A média de 70 polegadas fica no meio.
Etapa 3: Cada desvio padrão corresponde a uma distância de 2 polegadas.
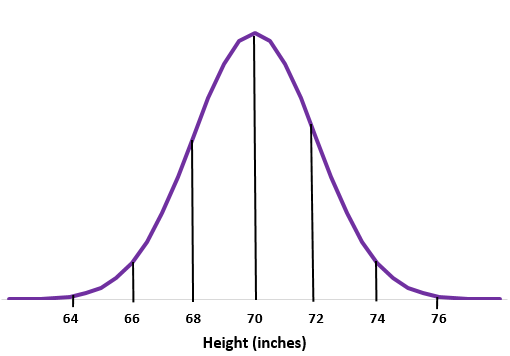
Exemplo 2: Suponha que o peso de uma certa espécie de lontra seja normalmente distribuído com média desvio padrão de
Etapa 1: esboce uma curva normal.
Passo 2: A média de 30 libras fica no meio.
Etapa 3: cada desvio padrão corresponde a uma distância de 5 libras
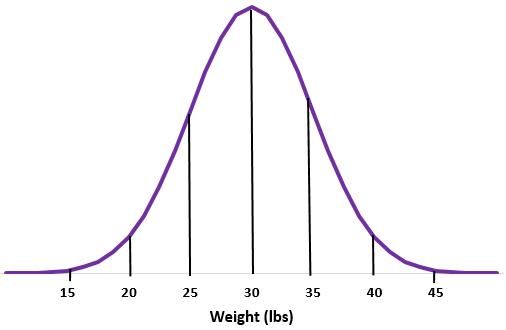
Como encontrar porcentagens usando a distribuição normal
A regra prática , às vezes chamada de regra 68-95-99,7 , afirma que, para uma variável aleatória normalmente distribuída, 68% dos dados estão dentro do intervalo de um desvio padrão da média, 95% estão dentro do intervalo de dois desvios padrão. desvios da média e 99,7% estão dentro de três desvios padrão da média.
Usando esta regra podemos responder perguntas sobre porcentagens.
Exemplo: Suponha que a altura dos homens em uma determinada escola seja normalmente distribuída com média desvio padrão de
Solução:
Etapa 1: esboce uma distribuição normal com média de desvio padrão de
Etapa 2: uma altura de 74 polegadas está dois desvios padrão acima da média. Adicione as porcentagens acima deste ponto à distribuição normal.
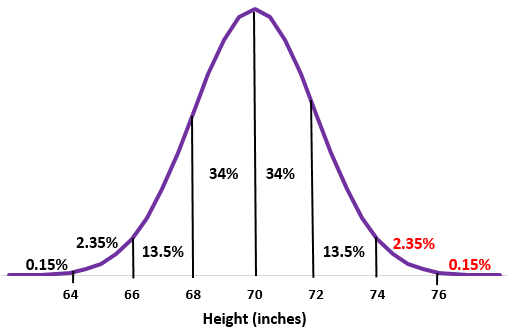
2,35% + 0,15% = 2,5%
Cerca de 2,5% dos homens nesta escola têm mais de 74 centímetros de altura.
Solução:
Etapa 1: esboce uma distribuição normal com média de desvio padrão de
Etapa 2: uma altura de 68 polegadas e 72 polegadas está um desvio padrão abaixo e acima da média, respectivamente. Basta somar as porcentagens entre esses dois pontos na distribuição normal.
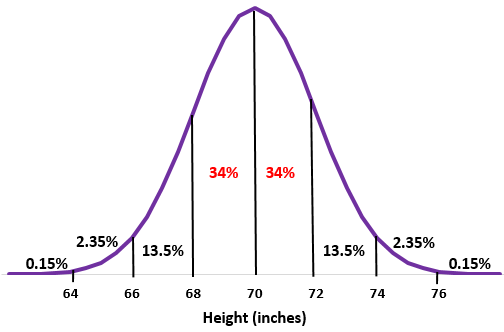
34% + 34% = 68%
Cerca de 68% dos homens nesta escola têm entre 68 e 72 polegadas de altura.
Como encontrar contagens usando a distribuição normal
Também podemos utilizar a regra prática para responder a perguntas sobre contagens.
Exemplo: Suponha que o peso de uma certa espécie de lontra seja normalmente distribuído com média desvio padrão de
Uma certa colônia tem 200 dessas lontras. Aproximadamente quantas dessas lontras pesam mais de 35 quilos?
Solução:
Etapa 1: esboce uma distribuição normal com média de desvio padrão de
Passo 2: Um peso de 35 libras está um desvio padrão acima da média. Adicione as porcentagens acima deste ponto à distribuição normal.
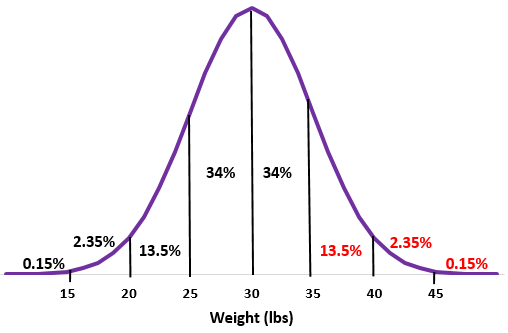
13,5% + 2,35% + 0,15% = 16%
Passo 3: Como existem 200 lontras na colônia, 16% de 200 = 0,16 * 200 = 32
Cerca de 32 lontras nesta colônia pesam mais de 35 quilos.
Aproximadamente quantas lontras nesta colônia pesam menos de 30 libras?
Em vez de seguir todos os passos que acabámos de seguir acima, podemos reconhecer que a mediana de uma distribuição normal é igual à média, que neste caso é de 30 libras.
Isso significa que metade das lontras pesa mais de 30 quilos e a outra metade pesa menos de 30 quilos. Isso significa que 50% das 200 lontras pesam menos de 30 libras, então 0,5 * 200 = 100 lontras .
Recursos adicionais
Os tutoriais a seguir fornecem informações adicionais sobre a distribuição normal:
6 exemplos concretos da distribuição normal
Distribuição normal vs distribuição t: a diferença
Como criar uma curva em forma de sino no Excel
Como criar uma curva em forma de sino em Python
About Author
Dr. benjamim anderson
Olá, sou Benjamin, um professor aposentado de estatística que se tornou professor dedicado na Statorials. Com vasta experiência e conhecimento na área de estatística, estou empenhado em compartilhar meu conhecimento para capacitar os alunos por meio de Statorials. Saber mais