A variância pode ser negativa?

Nas estatísticas, o termo variância refere-se a como os valores são distribuídos em um determinado conjunto de dados.

Uma pergunta comum que os alunos fazem sobre a variância é:

A variância pode ser negativa?

A resposta: Não, a variância não pode ser negativa. O valor mais baixo que pode assumir é zero.

Para entender por que isso acontece, precisamos entender como a variância é realmente calculada.

Como calcular a lacuna

A fórmula para encontrar a variância de uma amostra (denotada por s ² ) é:

s ² = Σ ( _xi – x ) ² / (n-1)

Ouro:

• x : A amostra significa
• x _i : A ^i-ésima observação na amostra
• N : Tamanho da amostra
• Σ : Um símbolo grego que significa “soma”

Por exemplo, suponha que temos o seguinte conjunto de dados com 10 valores:

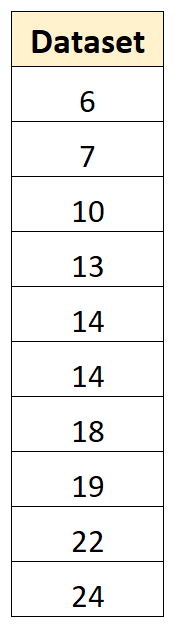
Podemos usar as seguintes etapas para calcular a variância desta amostra:

Etapa 1: Encontre a média

A média é simplesmente a média. Isso resulta em 14,7 .

Etapa 2: Encontre os desvios quadrados

Então podemos calcular o desvio quadrado de cada valor individual da média.

Por exemplo, o primeiro desvio quadrado é calculado como (6-14,7) ² = 75,69.

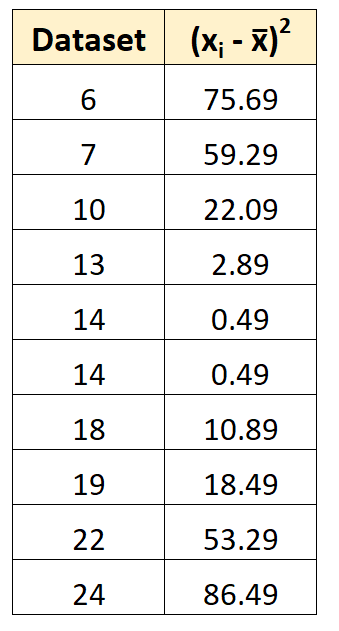
Etapa 3: Encontre a soma dos desvios quadrados

Então podemos somar todos os quadrados dos desvios:

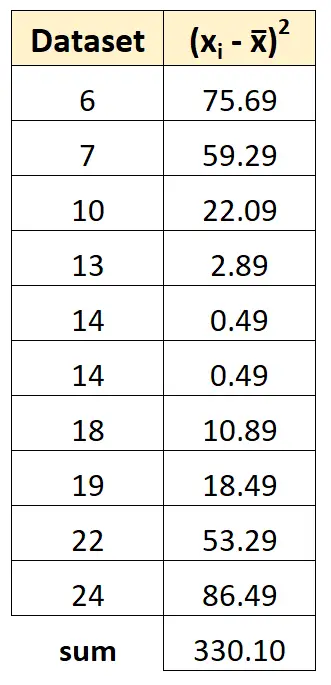
Etapa 4: calcular a variação da amostra

Finalmente, podemos calcular a variância amostral como a soma dos desvios quadrados dividida por (n-1):

s ² = 330,1 / (10-1) = 330,1 / 9 = 36,678

A variância da amostra é 36.678 .

Um exemplo de variância zero

A única maneira de um conjunto de dados ter variação zero é se todos os valores no conjunto de dados forem iguais .

Por exemplo, o seguinte conjunto de dados tem uma variação amostral igual a zero:

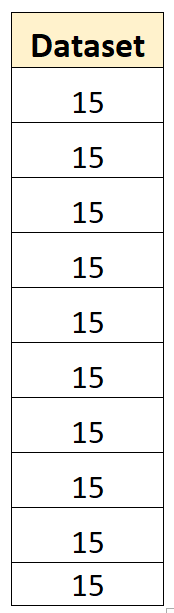
A média do conjunto de dados é 15 e nenhum dos valores individuais se desvia da média. Assim, a soma dos quadrados dos desvios será zero e a variância da amostra será simplesmente zero.

O desvio padrão pode ser negativo?

Uma forma mais comum de medir a distribuição de valores em um conjunto de dados é usar o desvio padrão, que é simplesmente a raiz quadrada da variância.

Por exemplo, se a variância de uma determinada amostra for ^s2 = 36,678 , então o desvio padrão (escrito s ) é calculado da seguinte forma:

s = √ ^s2 = √ 36,678 = 6,056

Como já sabemos que a variância é sempre zero ou um número positivo, isso significa que o desvio padrão nunca pode ser negativo, pois a raiz quadrada de zero ou de um número positivo não pode ser negativa.

Recursos adicionais

Medidas de tendência central: definição e exemplos
Medidas de dispersão: definição e exemplos