O que é d de somers? (definição e #038; exemplo)

Somers’ D , abreviação de Somers’ Delta, é uma medida da força e direção da associação entre uma variável dependente ordinal e uma variável independente ordinal.

Uma variável ordinal é aquela em que os valores possuem uma ordem natural (ex.: “ruim”, “neutro”, “bom”).

O valor de D de Somers está entre -1 e 1 onde:

• -1: Indica que todos os pares de variáveis não concordam
• 1: indica que todos os pares de variáveis correspondem

O D de Somers é usado na prática para muitos métodos estatísticos não paramétricos.

D de Somers: definição

Dadas duas variáveis, X e Y, podemos dizer:

• Dois pares (x _i , y _i ) e (x _j , y _j ) são concordantes se as classificações dos dois elementos corresponderem.
• Dois pares (x _i , y _i ) e (x _j , y _j ) são discordantes se as classificações dos dois elementos corresponderem.

Podemos então calcular o D de Somers usando a seguinte fórmula:

D de Somers = ( _NC – N _D ) / ( _NC + N _D + N _T )

Ouro:

• N _C : O número de pares correspondentes
• _ND : O número de pares discordantes
• N _T : O número de pares empatados

O valor resultante estará sempre entre -1 e 1.

D de Somers: exemplo em R

Suponha que uma mercearia queira avaliar a relação entre as duas variáveis ordinais a seguir:

• Simpatia geral do caixa (classificado de 1 a 3)
• Satisfação geral com a experiência do cliente (também classificada de 1 a 3)

Eles coletam as seguintes classificações de uma amostra de 10 clientes:

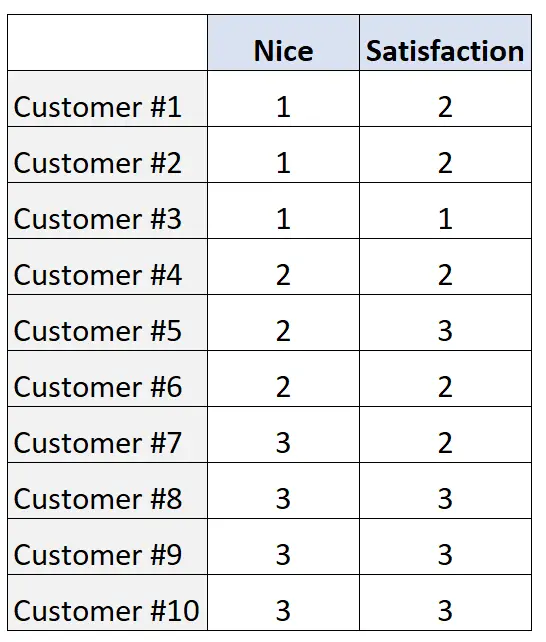
Para quantificar a relação entre as duas variáveis, podemos calcular o D de Somers usando o seguinte código em R:

 #enter data
nice <- c(1, 1, 1, 2, 2, 2, 3, 3, 3, 3)
satisfaction <- c(2, 2, 1, 2, 3, 2, 2, 3, 3, 3)

#load DescTools package
library(DescTools)

#calculate Somers' D
SomersDelta(nice, satisfaction)

[1] 0.6896552

O D de Somers é 0,6896552 .

Sendo este valor bastante próximo de 1, indica que existe uma relação positiva bastante forte entre as duas variáveis.

Isso faz sentido intuitivamente: os clientes que classificam os caixas como mais gentis também tendem a avaliar sua satisfação geral mais alta.

Recursos adicionais

Uma introdução ao coeficiente de correlação de Pearson
Uma introdução ao Tau de Kendall