Amostragem estratificada

Neste artigo explicamos o que é a amostragem estratificada e como ela é realizada. Aqui você encontrará a explicação dos subtipos de amostragem estratificada e, finalmente, quais são as vantagens e desvantagens da amostragem estratificada.

O que é amostragem estratificada?

A amostragem estratificada é um método estatístico usado para selecionar elementos de uma amostra dividindo a população em grupos (chamados estratos). Ou seja, na amostragem estratificada, a população é dividida em estratos e os indivíduos de cada estrato são selecionados aleatoriamente para formar toda a amostra do estudo.

Estratos são grupos homogêneos, ou seja, os indivíduos de um estrato possuem características próprias que os diferenciam dos demais estratos. Um indivíduo, portanto, só pode pertencer a um estrato.

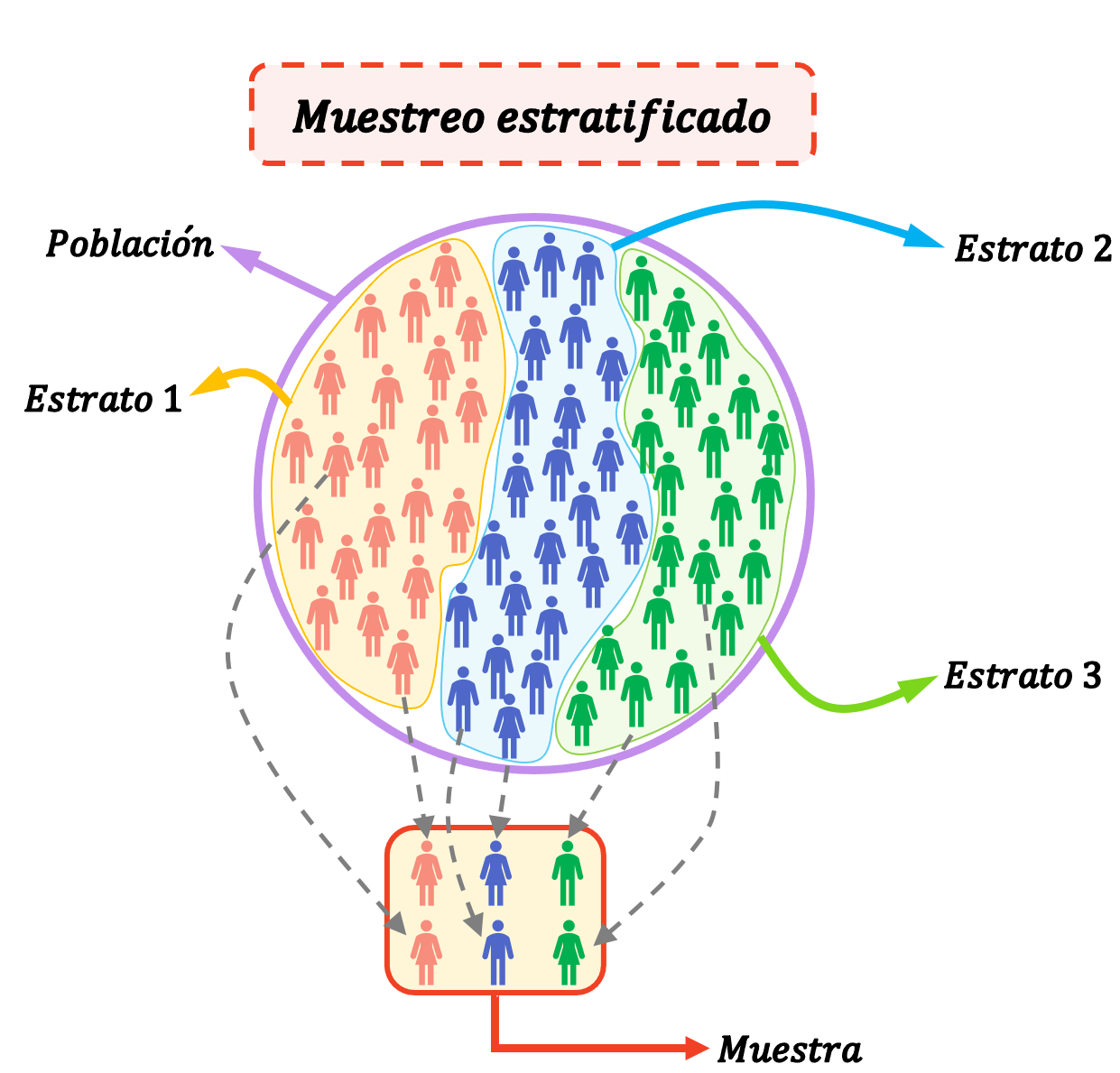
A amostragem estratificada é muito útil quando a população é composta por grupos muito homogêneos e muito diferentes entre si.

Logicamente, a soma do tamanho de todos os estratos dá o tamanho da população estatística:

Da mesma forma, a soma do tamanho da amostra escolhido em cada estrato é igual ao tamanho total da amostra do estudo estatístico:

Geralmente diferenciamos letras maiúsculas e minúsculas para designar a população ou amostra, respectivamente.

Como fazer amostragem estratificada

As etapas para realizar a amostragem estratificada são as seguintes:

1. Defina a população-alvo.
2. Escolha a estratificação da variável e quantos estratos haverá.
3. Identifique a qual estrato pertence cada elemento da população.
4. Calcule o tamanho de cada estrato que fará parte da amostra.
5. Selecionar aleatoriamente os elementos de cada estrato que pertencerão à amostra do estudo. Para cada estrato devem ser selecionados tantos elementos quantos foram decididos na etapa anterior.

Tenha em mente que o tamanho que cada estrato representará na amostra depende não apenas do tamanho do estrato, mas também do tipo de amostragem estratificada. A seguir, é explicado cada tipo de amostragem estratificada e como o tamanho da amostra de cada estrato é calculado por meio de um exemplo.

Tipos de amostragem estratificada

Agora que você conhece a definição de amostragem estratificada, deve saber que existem vários tipos de amostragem estratificada, que são classificados da seguinte forma:

• Amostragem estratificada proporcional
• Amostragem Estratificada Uniforme
• A amostragem é ótima

Cada tipo de amostragem estratificada é explicado em detalhes abaixo para melhor compreender o significado de cada um.

Amostragem estratificada proporcional

Na amostragem estratificada proporcional , ou amostragem de alocação proporcional, o número de elementos de cada estrato que fazem parte da amostra do estudo é proporcional ao tamanho de cada estrato.

Assim, se um estrato for maior que outro, a amostra final conterá mais elementos desse estrato. Por outro lado, se um estrato for menor que outro, haverá menos elementos deste estrato na amostra de análise estatística.

Este tipo de amostragem estratificada é útil quando os estratos têm tamanhos diferentes e queremos que a amostra inclua mais elementos dos estratos maiores.

Para calcular o número de elementos de cada estrato que estarão na amostra, o tamanho de cada estrato deve ser dividido pela soma dos tamanhos de todos os estratos. O resultado será a proporção do estrato que deverá ser incluída na amostra, portanto deverá ser multiplicada pelo tamanho de amostra desejado.

Ouro

é o tamanho total da amostra desejado,

o número de elementos no estrato

ser incluído na amostra,

tamanho do estrato

, E

o número total de elementos da população.

Por exemplo, imagine que quiséssemos fazer um estudo numa empresa com 150 trabalhadores, pegando numa amostra de 50 pessoas e estratificando os dados com base na idade dos trabalhadores. Podemos classificar os dados da seguinte forma:

• De 20 a 29 anos: 35 trabalhadores
• De 30 a 39 anos: 57 funcionários
• De 40 a 49 anos: 42 funcionários
• De 50 a 59 anos: 16 funcionários

Assim, se estratificarmos os dados proporcionalmente, a amostragem será a seguinte:

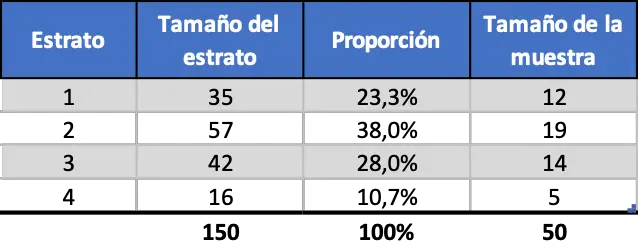
Amostragem Estratificada Uniforme

Na amostragem estratificada uniforme , ou amostragem por afixação uniforme, o número de elementos de cada estrato que fazem parte da amostra do estudo é igual.

Cada estrato tem, portanto, o mesmo peso neste tipo de amostragem. Quer um estrato tenha mais ou menos indivíduos que outro estrato, todos serão representados na amostra pelo mesmo número de indivíduos.

Neste caso, para calcular o tamanho dos elementos de cada estrato, o tamanho da amostra desejado deve ser dividido pelo número de estratos existentes. Em outras palavras, a seguinte fórmula deve ser usada:

Ouro

é o tamanho total da amostra desejado,

o número de elementos no estrato

quem será incluído na amostra, e

o número de estratos em que a população foi dividida.

Seguindo o exemplo anterior, como queríamos uma amostra de 50 trabalhadores e no total havia 4 estratos diferentes, o tamanho da amostra de cada estrato será:

Sendo o resultado um número decimal, alguns estratos terão 12 trabalhadores e outros 13 até chegar a 50 trabalhadores. Portanto, a amostragem estratificada uniforme é a seguinte:

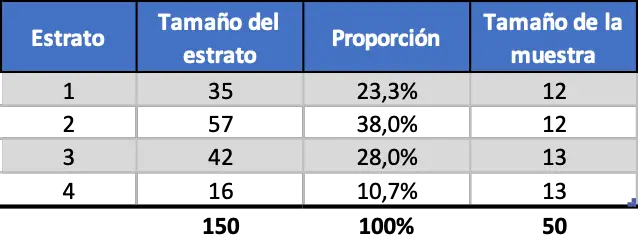
Como você pode ver, o tamanho da amostra de cada estrato independe da proporção de cada um.

Amostragem estratificada ideal

Na amostragem estratificada ótima , o número de elementos em cada estrato depende proporcionalmente da variabilidade de cada estrato.

Assim, os estratos com maior variabilidade terão um tamanho amostral maior, e vice-versa, os estratos com menor variabilidade terão um tamanho amostral menor.

A fórmula para determinar quantos elementos de cada estrato farão parte da amostra estatística do estudo é a seguinte:

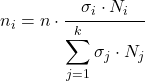
Ouro

é o tamanho total da amostra desejado,

é o número de elementos no estrato

ser incluído na amostra,

é o desvio padrão (ou desvio típico) do estrato

, E

é o tamanho do estrato

.

Vantagens e desvantagens da amostragem estratificada

A amostragem estratificada tem as seguintes vantagens e desvantagens:

vantagem	Desvantagens
Permite estudar estatisticamente não só toda a população, mas também cada estrato específico.	Este é um método de amostragem complicado de implementar.
O erro amostral cometido pela amostragem estratificada é sempre igual ou menor que o da amostragem aleatória simples.	Este é um processo de amostragem demorado e, portanto, caro.
Permite aproveitar o conhecimento do pesquisador sobre a população.	São necessárias muitas informações sobre a amostra analisada para poder estratificá-la.
Com a amostragem estratificada, garantimos que pelo menos um elemento de cada estrato seja incluído na amostra.	É necessário conhecer a proporção de cada estrato para poder realizar a amostragem.

A principal característica da amostragem estratificada é que ela serve para analisar estatisticamente cada grupo ou estrato em que a população foi dividida. É claro que toda a população também pode ser estudada com este tipo de amostragem. Além disso, os benefícios da estratificação dos dados serão maiores se os estratos forem diferentes entre si.

Pelo contrário, o facto de estratificar os dados para poder realizar a amostragem implica um aumento na complexidade da amostragem, sendo a amostragem estratificada mais complicada de realizar em comparação com outros tipos de amostragem. Esta propriedade também implica que é uma amostra cara, pois leva tempo para fazer a estratificação corretamente.

Outra desvantagem da amostragem estratificada é que ela requer muitas informações sobre a população que se deseja estudar, o que não é necessário em outros tipos de amostragem, como a amostragem aleatória simples. Embora esta desvantagem possa ser mitigada se o pesquisador tiver grande conhecimento na área.

Por fim, com a amostragem estratificada, obtemos uma amostra mais representativa da população do que em outros tipos de amostragem, porque garantimos a inclusão de elementos de cada estrato. Em contrapartida, em outras amostras, a amostra resultante não pode conter quaisquer elementos de nenhum estrato.