Análise de componentes principais em r: exemplo passo a passo

A análise de componentes principais, muitas vezes abreviada como PCA, é uma técnica de aprendizado de máquina não supervisionada que busca encontrar os componentes principais – combinações lineares dos preditores originais – que explicam uma grande parte da variação em um conjunto de dados.

O objetivo da PCA é explicar a maior parte da variabilidade em um conjunto de dados com menos variáveis do que o conjunto de dados original.

Para um determinado conjunto de dados com p variáveis, poderíamos examinar os gráficos de dispersão de cada combinação de variáveis aos pares, mas o número de gráficos de dispersão pode se tornar grande muito rapidamente.

Para preditores p , existem nuvens de pontos p(p-1)/2.

Portanto, para um conjunto de dados com p = 15 preditores, haveria 105 gráficos de dispersão diferentes!

Felizmente, o PCA oferece uma maneira de encontrar uma representação de baixa dimensão de um conjunto de dados que capture o máximo possível da variação dos dados.

Se pudermos capturar a maior parte da variação em apenas duas dimensões, poderemos projetar todas as observações do conjunto de dados original em um gráfico de dispersão simples.

A forma como encontramos os componentes principais é a seguinte:

_{Dado um conjunto de dados com} p _preditores : _

• _{Z m = ΣΦ jm _}
• Z ₁ é a combinação linear de preditores que captura o máximo de variação possível.
• Z ₂ é a próxima combinação linear de preditores que captura a maior variância enquanto é ortogonal (ou seja, não correlacionada) a Z ₁ .
• Z ₃ é então a próxima combinação linear de preditores que captura a maior variação enquanto é ortogonal a Z ₂ .
• E assim por diante.

Na prática, usamos as seguintes etapas para calcular as combinações lineares dos preditores originais:

1. Dimensione cada uma das variáveis para obter uma média de 0 e um desvio padrão de 1.

2. Calcule a matriz de covariância para as variáveis escalonadas.

3. Calcule os autovalores da matriz de covariância.

Usando álgebra linear, podemos mostrar que o autovetor que corresponde ao maior autovalor é o primeiro componente principal. Em outras palavras, esta combinação específica de preditores explica a maior variação nos dados.

O autovetor correspondente ao segundo maior autovalor é o segundo componente principal e assim por diante.

Este tutorial fornece um exemplo passo a passo de como realizar esse processo em R.

Etapa 1: carregar dados

Primeiro carregaremos o pacote Tidyverse , que contém várias funções úteis para visualizar e manipular dados:

 library (tidyverse)

Para este exemplo, usaremos o conjunto de dados USArrests incorporado ao R, que contém o número de prisões por 100.000 residentes em cada estado dos EUA em 1973 por assassinato , agressão e estupro .

Inclui também o percentual da população de cada estado que vive em áreas urbanas, UrbanPop .

O código a seguir mostra como carregar e exibir as primeiras linhas do conjunto de dados:

 #load data
data ("USArrests")

#view first six rows of data
head(USArrests)

           Murder Assault UrbanPop Rape
Alabama 13.2 236 58 21.2
Alaska 10.0 263 48 44.5
Arizona 8.1 294 80 31.0
Arkansas 8.8 190 50 19.5
California 9.0 276 91 40.6
Colorado 7.9 204 78 38.7

Passo 2: Calcule os componentes principais

Depois de carregar os dados, podemos usar a função integrada prcomp() do R para calcular os componentes principais do conjunto de dados.

Certifique-se de especificar scale = TRUE para que cada uma das variáveis no conjunto de dados seja dimensionada para ter uma média de 0 e um desvio padrão de 1 antes de calcular os componentes principais.

Observe também que os autovetores em R apontam na direção negativa por padrão, então multiplicaremos por -1 para inverter os sinais.

 #calculate main components
results <- prcomp(USArrests, scale = TRUE )

#reverse the signs
results$rotation <- -1*results$rotation

#display main components
results$rotation

               PC1 PC2 PC3 PC4
Murder 0.5358995 -0.4181809 0.3412327 -0.64922780
Assault 0.5831836 -0.1879856 0.2681484 0.74340748
UrbanPop 0.2781909 0.8728062 0.3780158 -0.13387773
Rape 0.5434321 0.1673186 -0.8177779 -0.08902432

Podemos perceber que o primeiro componente principal (PC1) apresenta valores elevados para homicídio, agressão e estupro, indicando que este componente principal descreve a maior variação nessas variáveis.

Podemos observar também que o segundo componente principal (PC2) tem um valor alto para UrbanPop, indicando que este componente principal enfatiza a população urbana.

Observe que as pontuações dos componentes principais para cada estado são armazenadas em results$x . Também multiplicaremos essas pontuações por -1 para inverter os sinais:

 #reverse the signs of the scores
results$x <- -1*results$x

#display the first six scores
head(results$x)

                  PC1 PC2 PC3 PC4
Alabama 0.9756604 -1.1220012 0.43980366 -0.154696581
Alaska 1.9305379 -1.0624269 -2.01950027 0.434175454
Arizona 1.7454429 0.7384595 -0.05423025 0.826264240
Arkansas -0.1399989 -1.1085423 -0.11342217 0.180973554
California 2.4986128 1.5274267 -0.59254100 0.338559240
Colorado 1.4993407 0.9776297 -1.08400162 -0.001450164

Etapa 3: visualize os resultados com um biplot

A seguir, podemos criar um biplot – um gráfico que projeta cada uma das observações do conjunto de dados em um gráfico de dispersão que usa o primeiro e o segundo componentes principais como eixos:

Observe que scale = 0 garante que as setas no gráfico sejam dimensionadas para representar as cargas.

 biplot(results, scale = 0 )

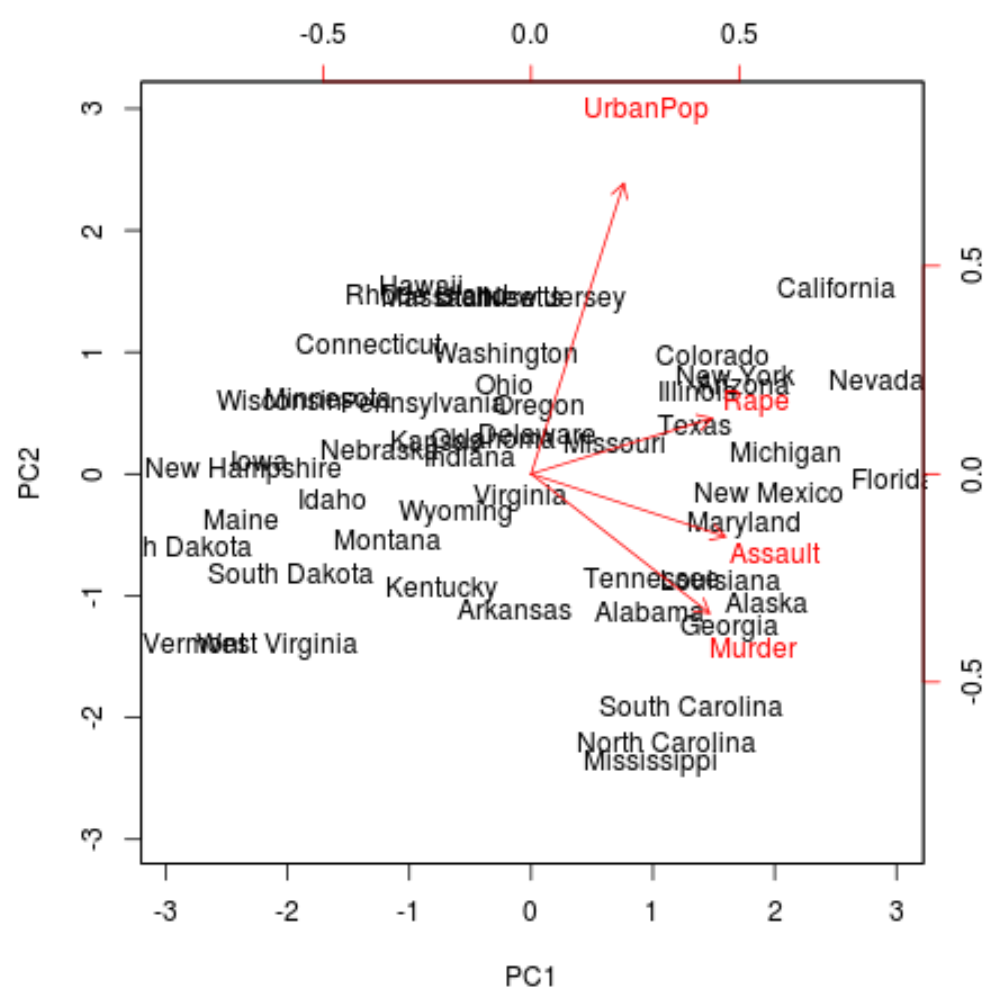
No gráfico podemos ver cada um dos 50 estados representados em um espaço bidimensional simples.

Os estados próximos uns dos outros no gráfico têm padrões de dados semelhantes em relação às variáveis no conjunto de dados original.

Podemos também ver que alguns estados estão mais fortemente associados a certos crimes do que outros. Por exemplo, a Geórgia é o estado mais próximo da variável Assassinato no gráfico.

Se olharmos para os estados com as maiores taxas de homicídios no conjunto de dados original, podemos ver que a Geórgia está realmente no topo da lista:

 #display states with highest murder rates in original dataset
head(USArrests[ order (-USArrests$Murder),])

               Murder Assault UrbanPop Rape
Georgia 17.4 211 60 25.8
Mississippi 16.1 259 44 17.1
Florida 15.4 335 80 31.9
Louisiana 15.4 249 66 22.2
South Carolina 14.4 279 48 22.5
Alabama 13.2 236 58 21.2

Etapa 4: Encontre a variação explicada por cada componente principal

Podemos usar o código a seguir para calcular a variação total no conjunto de dados original explicada por cada componente principal:

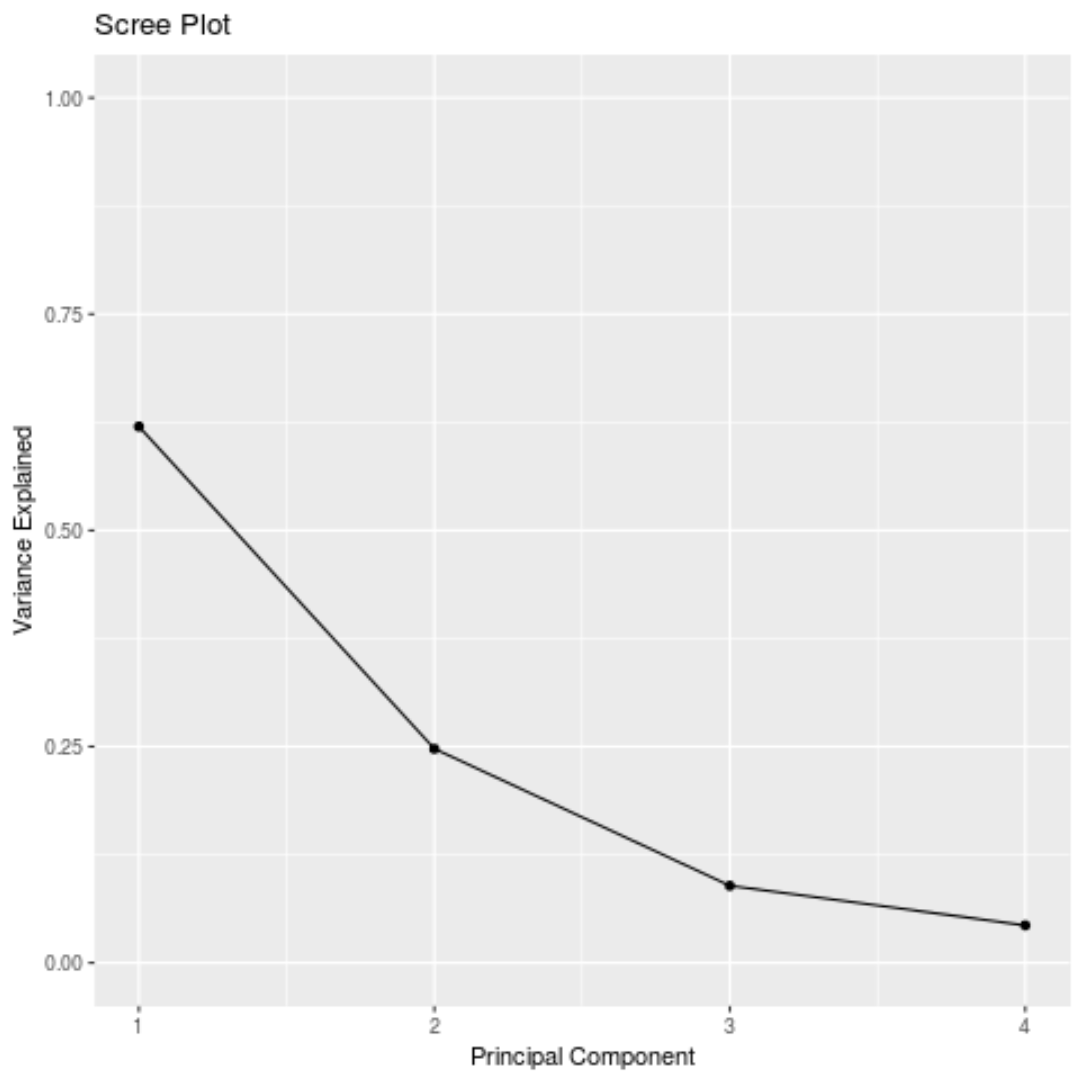
 #calculate total variance explained by each principal component
results$sdev^2 / sum (results$sdev^2)

[1] 0.62006039 0.24744129 0.08914080 0.04335752

A partir dos resultados, podemos observar o seguinte:

• O primeiro componente principal explica 62% da variação total no conjunto de dados.
• O segundo componente principal explica 24,7% da variação total do conjunto de dados.
• O terceiro componente principal explica 8,9% da variação total do conjunto de dados.
• O quarto componente principal explica 4,3% da variação total do conjunto de dados.

Assim, os dois primeiros componentes principais explicam a maior parte da variância total dos dados.

Isto é um bom sinal porque o biplot anterior projetou cada uma das observações dos dados originais em um gráfico de dispersão que levou em consideração apenas os dois primeiros componentes principais.

Assim, é válido examinar os padrões do biplot para identificar estados que sejam semelhantes entre si.

Também podemos criar um scree plot – um gráfico que exibe a variância total explicada por cada componente principal – para visualizar os resultados do PCA:

 #calculate total variance explained by each principal component
var_explained = results$sdev^2 / sum (results$sdev^2)

#create scree plot
qplot(c(1:4), var_explained) + 
  geom_line() + 
  xlab(" Principal Component ") + 
  ylab(" Variance Explained ") +
  ggtitle(" Scree Plot ") +
  ylim(0, 1) 

Análise de componentes principais na prática

Na prática, o PCA é usado com mais frequência por dois motivos:

1. Análise Exploratória de Dados – Usamos PCA quando exploramos pela primeira vez um conjunto de dados e queremos entender quais observações nos dados são mais semelhantes entre si.

2. Regressão de componentes principais – Também podemos usar o PCA para calcular componentes principais que podem então ser usados na regressão de componentes principais . Esse tipo de regressão é frequentemente usado quando há multicolinearidade entre os preditores em um conjunto de dados.

O código R completo usado neste tutorial pode ser encontrado aqui .