Como realizar análise de componentes principais no sas

A análise de componentes principais (PCA) é uma técnica de aprendizado de máquina não supervisionada que busca encontrar os componentes principais – combinações lineares de variáveis preditoras – que explicam uma grande parte da variação em um conjunto de dados.

A maneira mais simples de realizar PCA no SAS é usar a instrução PROC PRINCOMP , que utiliza a seguinte sintaxe básica:

 proc princomp data =my_data out =out_data outstat =stats;
    var var1 var2 var3;
run ;

Aqui está o que cada instrução faz:

• data : o nome do conjunto de dados a ser usado para o PCA
• out : o nome do conjunto de dados a ser criado que contém todos os dados originais mais as pontuações dos componentes principais
• outstat : especifica que um conjunto de dados deve ser criado contendo médias, desvios padrão, coeficientes de correlação, valores próprios e vetores próprios.
• var : as variáveis a serem usadas para PCA do conjunto de dados de entrada.

O exemplo passo a passo a seguir mostra como usar a instrução PROC PRINCOMP na prática para realizar análise de componentes principais no SAS.

Etapa 1: crie um conjunto de dados

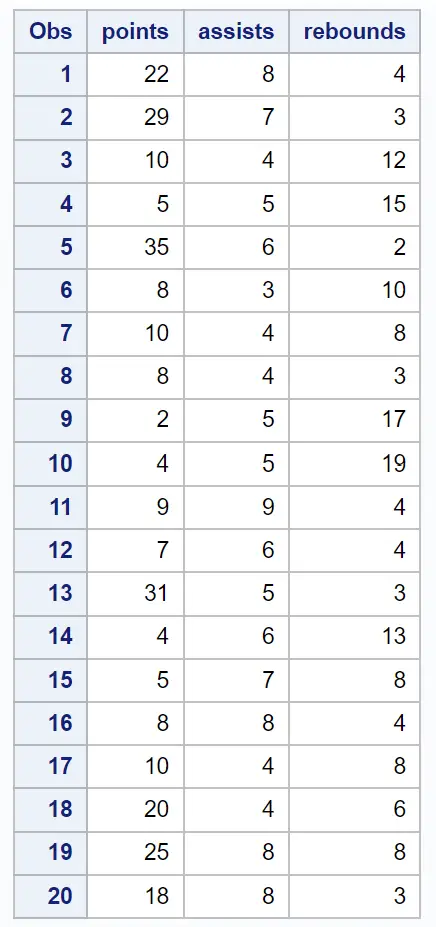
Suponha que temos o seguinte conjunto de dados contendo diversas informações sobre 20 jogadores de basquete:

 /*create dataset*/
data my_data;
    input points assists rebounds;
    datalines ;
22 8 4
29 7 3
10 4 12
5 5 15
35 6 2
8 3 10
10 4 8
8 4 3
2 5 17
4 5 19
9 9 4
7 6 4
31 5 3
4 6 13
5 7 8
8 8 4
10 4 8
20 4 6
25 8 8
18 8 3
;
run ;

/*view dataset*/
proc print data =my_data; 

Passo 2: Realizar análise de componentes principais

Podemos usar a instrução PROC PRINCOMP para realizar a análise de componentes principais usando as variáveis points , assists e bounces do conjunto de dados:

 /*perform principal components analysis*/
proc princomp data =my_data out =out_data outstat =stats;
    var points assists rebounds;
run ;

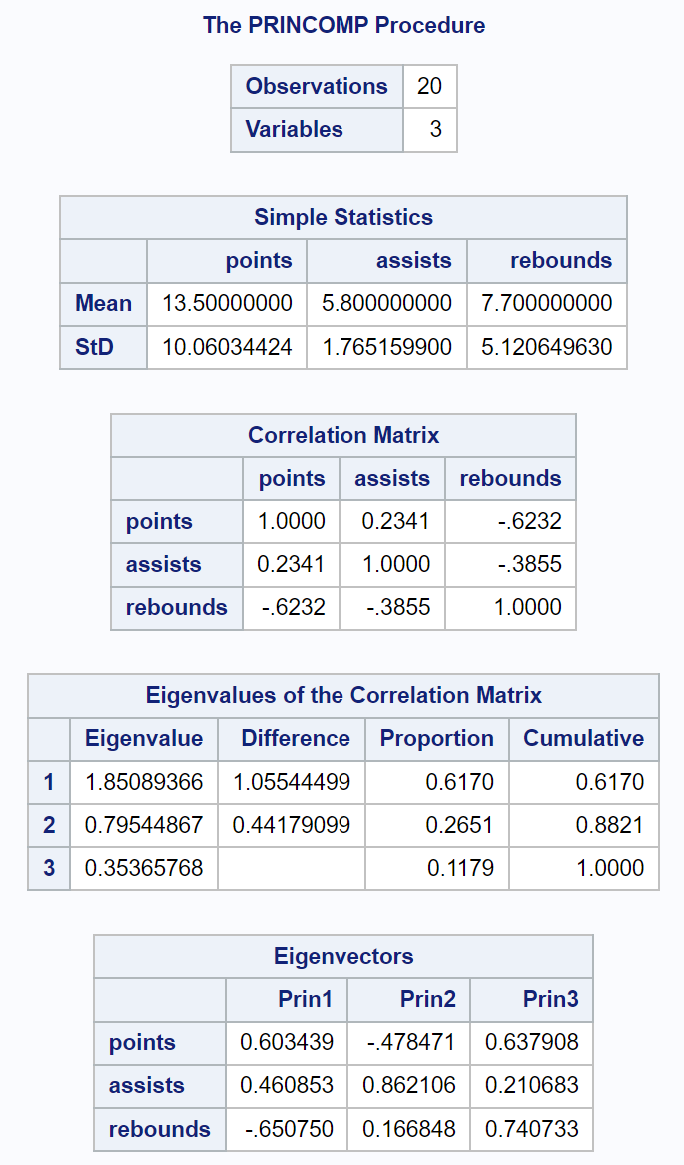
A primeira parte da saída exibe várias estatísticas descritivas, incluindo a média e os desvios padrão de cada variável de entrada, uma matriz de correlação e os valores dos autovalores e autovetores:

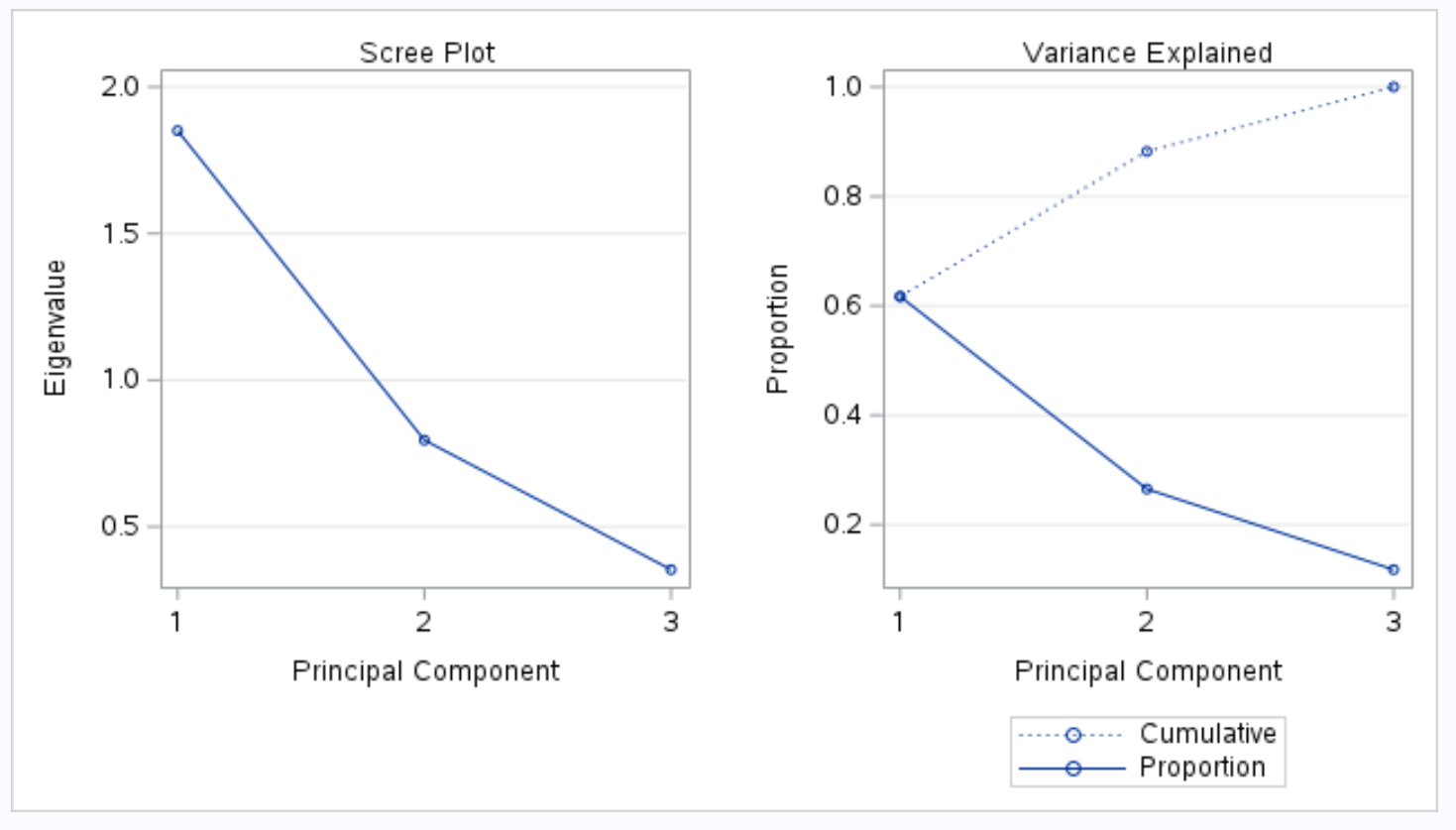
A próxima parte da saída exibe um gráfico de scree e um gráfico de variância explicado :

Quando realizamos PCA, muitas vezes queremos entender qual porcentagem da variação total no conjunto de dados pode ser explicada por cada componente principal.

A tabela resultante intitulada Autovalores da Matriz de Correlação nos permite ver exatamente qual porcentagem da variação total é explicada por cada componente principal:

• O primeiro componente principal explica 61,7% da variação total do conjunto de dados.
• O segundo componente principal explica 26,51% da variação total do conjunto de dados.
• O terceiro componente principal explica 11,79% da variação total do conjunto de dados.

Observe que todas as porcentagens somam 100%.

O gráfico intitulado Variância Explicada nos permite visualizar esses valores.

O eixo x exibe o componente principal e o eixo y exibe a porcentagem da variância total explicada por cada componente principal individual.

Etapa 3: Crie um biplot para visualizar os resultados

Para visualizar os resultados do PCA para um determinado conjunto de dados, podemos criar um biplot , que é um gráfico que exibe cada observação em um conjunto de dados em um plano formado pelos dois primeiros componentes principais.

Podemos usar a seguinte sintaxe no SAS para criar um biplot:

 /*create dataset with column called obs to represent row numbers of original data*/
data biplot_data;
   set out_data;
   obs=_n_;
run ;

/*create biplot using values from first two principal components*/
proc sgplot data =biplot_data;
    scatter x =Prin1 y =Prin2 / datalabel =obs;
run ; 

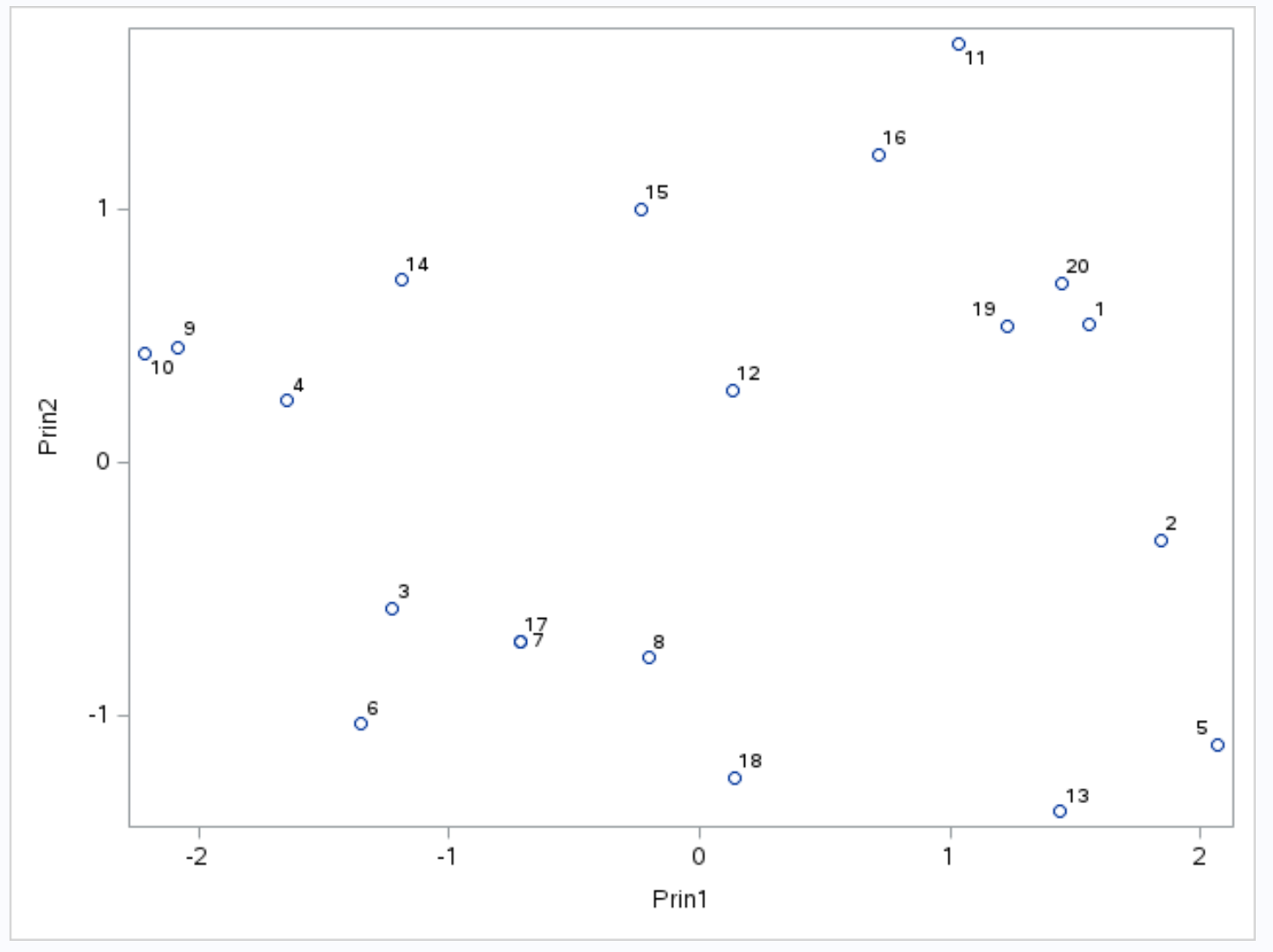
O eixo x exibe o primeiro componente principal, o eixo y exibe o segundo componente principal e as observações individuais do conjunto de dados são exibidas dentro do gráfico como pequenos círculos.

As observações que estão lado a lado no gráfico possuem valores semelhantes para as três variáveis de pontos , assistências e rebotes .

Por exemplo, na extremidade esquerda do gráfico, podemos ver que as observações nº 9 e nº 10 estão extremamente próximas uma da outra.

Se nos referirmos ao conjunto de dados original, podemos ver os seguintes valores para estas observações:

• Observação nº 9 : 2 pontos, 5 assistências, 17 rebotes
• Observação #10 : 4 pontos, 5 assistências, 19 rebotes

Os valores são semelhantes para cada uma das três variáveis, o que explica porque essas observações estão tão próximas umas das outras no biplot.

Também vimos na tabela de resultados intitulada Valores próprios da matriz de correlação que os dois primeiros componentes principais respondem por 88,21% da variação total no conjunto de dados.

Como esse percentual é muito alto, é válido analisar quais observações do biplot estão próximas uma da outra, pois os dois componentes principais que compõem o biplot respondem por quase toda a variação do conjunto de dados.

Recursos adicionais

Os tutoriais a seguir explicam como executar outras tarefas comuns no SAS:

Como realizar regressão linear simples no SAS
Como realizar regressão linear múltipla no SAS
Como realizar regressão logística no SAS