Análise univariada ou multivariada: qual a diferença?

O termo análise univariada refere-se à análise de uma variável. Você pode se lembrar disso porque o prefixo “uni” significa “um”.

O termo análise multivariada refere-se à análise de mais de uma variável. Você pode se lembrar disso porque o prefixo “multi” significa “mais de um”.

Existem três maneiras comuns de realizar análises univariadas :

1. Estatísticas resumidas

• Podemos calcular medidas de tendência central como a média ou mediana de uma variável.
• Também podemos calcular medidas de dispersão, como o desvio padrão de uma variável.

2. Distribuições de frequência

• Podemos criar uma distribuição de frequência , que descreve a frequência com que cada valor aparece para uma variável.

3. Gráficos

• Podemos criar gráficos como boxplots, histogramas, gráficos de densidade, etc. para visualizar a distribuição dos valores de uma variável.

Existem duas maneiras comuns de realizar análise multivariada :

1. Matriz de gráfico de dispersão

• Podemos criar uma matriz de gráfico de dispersão, que nos permite visualizar a relação entre cada combinação de variáveis em pares em um conjunto de dados.

2. Algoritmos de aprendizado de máquina

• Podemos usar um algoritmo de aprendizado supervisionado para ajustar um modelo como a regressão linear múltipla , que quantifica a relação entre múltiplas variáveis preditoras e uma variável de resposta.
• Também podemos usar um algoritmo de aprendizagem não supervisionado, como a análise de componentes principais, para encontrar simultaneamente a estrutura e as relações entre múltiplas variáveis em um conjunto de dados.

Os exemplos a seguir mostram como realizar análises univariadas e multivariadas com o seguinte conjunto de dados:

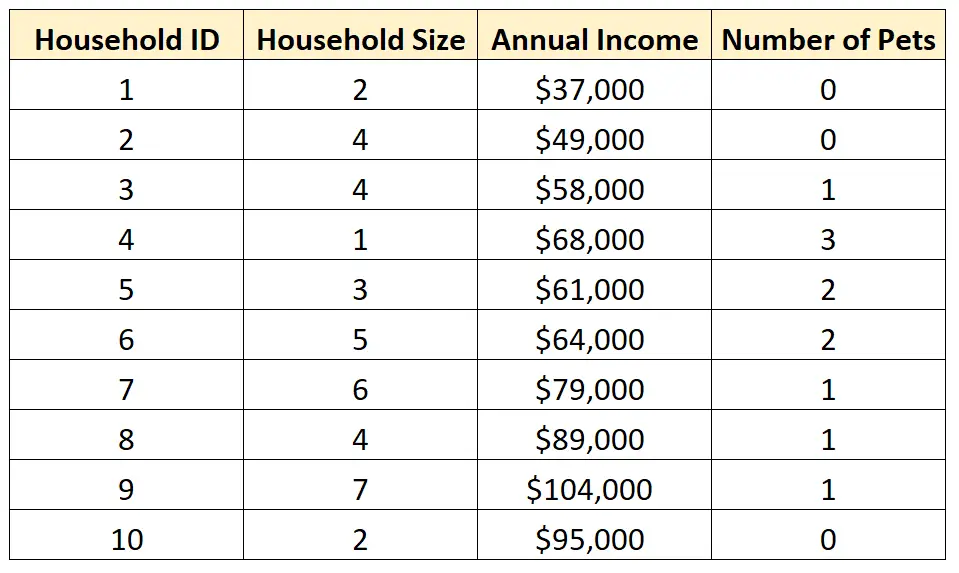
Nota : Quando você analisa exatamente duas variáveis, chama-se análise bivariada .

Exemplo: como realizar análise univariada

Poderíamos optar por realizar uma análise univariada em qualquer uma das variáveis individuais do conjunto de dados.

Por exemplo, podemos optar por realizar uma análise univariada sobre a variável Tamanho do agregado familiar :

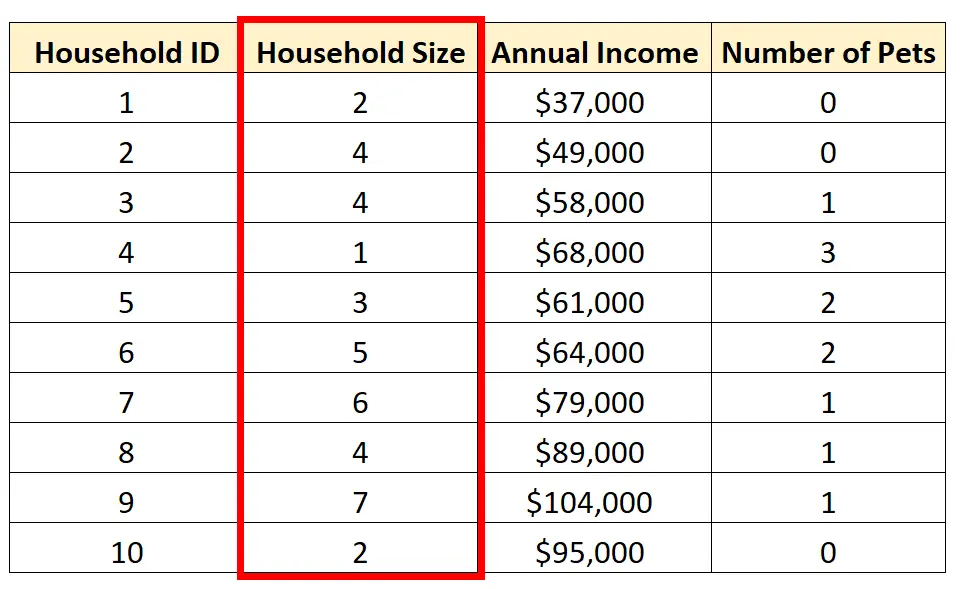
Podemos calcular as seguintes medidas de tendência central do tamanho do agregado familiar:

• Média (o valor médio): 3,8
• Mediana (o valor médio): 4

Esses valores nos dão uma ideia de onde está o valor “central”.

Também podemos calcular as seguintes medidas de dispersão:

• Faixa (a diferença entre máximo e mínimo): 6
• Escala interquartil (a distribuição dos 50% intermediários dos valores): 2,5
• Desvio padrão (uma medida média de spread): 1,87

Esses valores nos dão uma ideia da distribuição dos valores desta variável.

Também podemos criar a seguinte tabela de distribuição de frequência para resumir a frequência com que ocorrem valores diferentes:

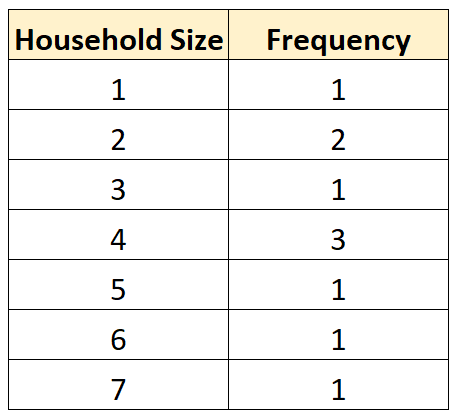
Também podemos criar um boxplot para visualizar a distribuição dos valores de acordo com o tamanho do domicílio:

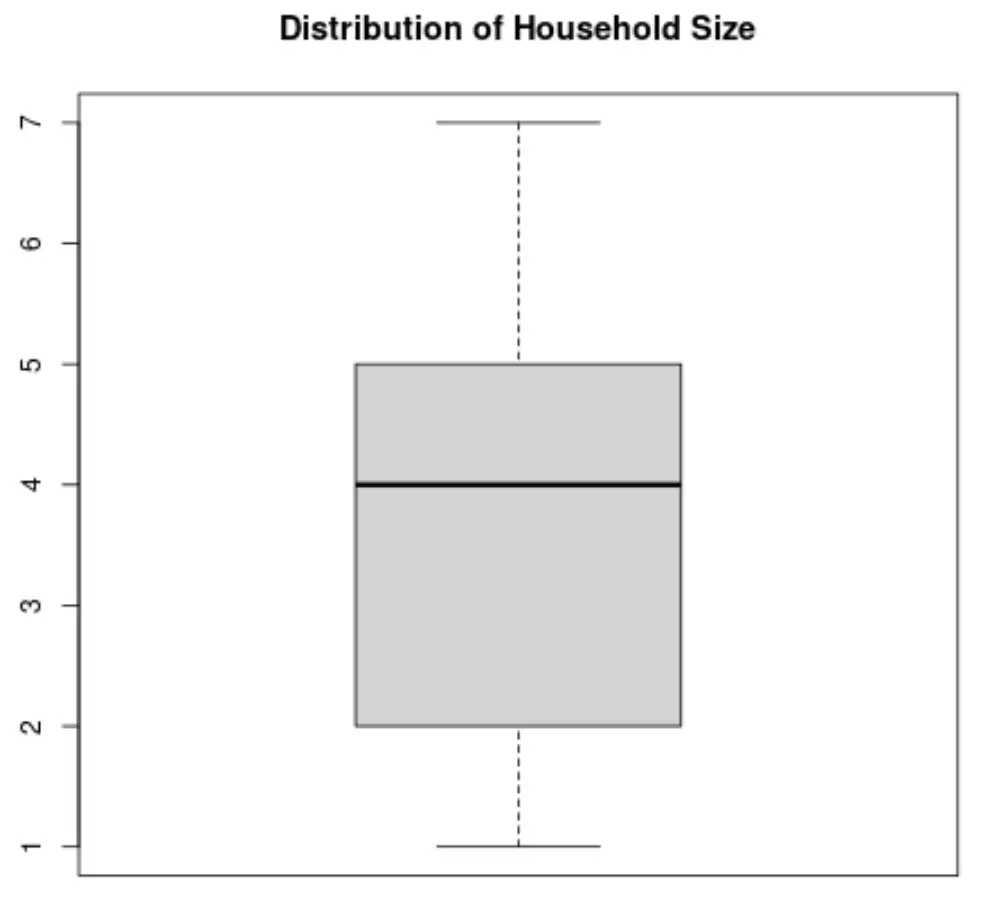
Alternativamente, poderíamos criar um histograma para visualizar a distribuição dos valores:

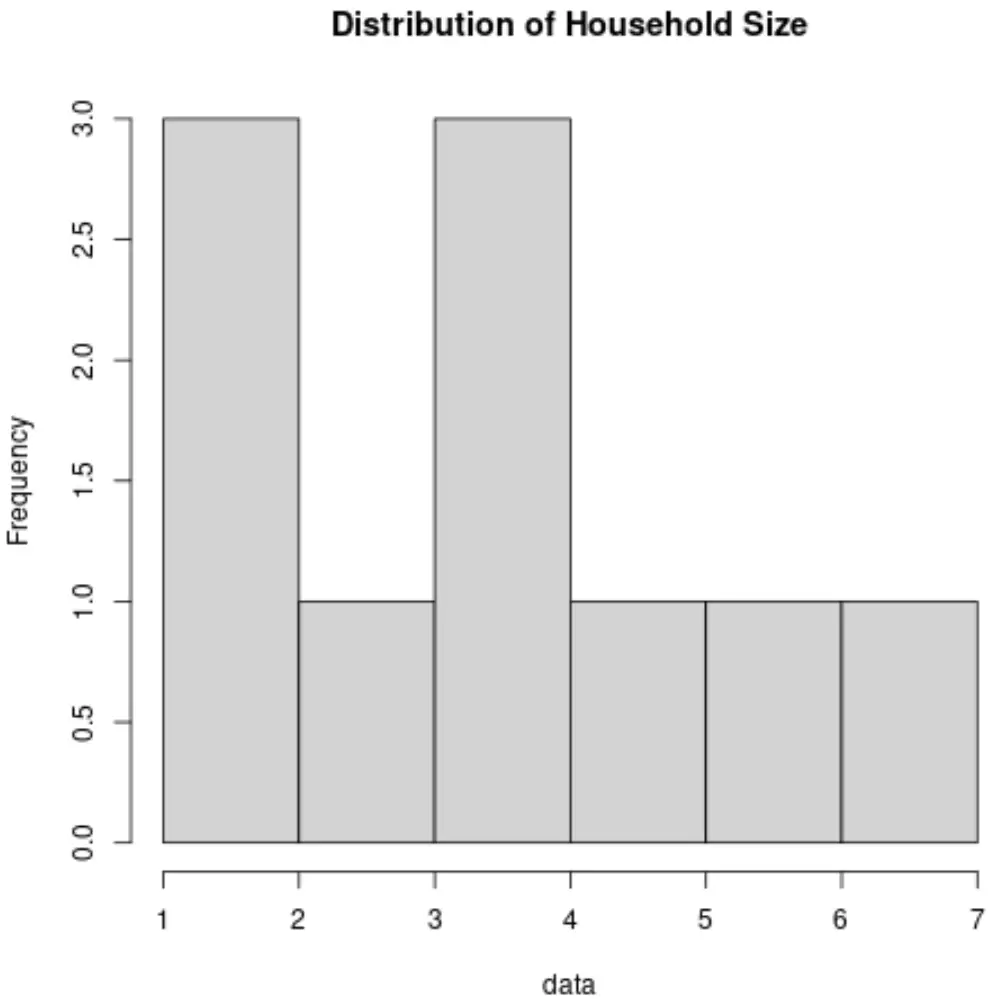
Calculando essas medidas e criando esses gráficos, podemos entender melhor como os valores estão distribuídos para a variável Tamanho do Domicílio.

Exemplo: como realizar análise multivariada

Vamos supor novamente que temos o mesmo conjunto de dados:

Uma forma simples de análise multivariada que poderíamos realizar neste conjunto de dados é criar uma matriz de gráfico de dispersão , que é uma matriz que mostra um gráfico de dispersão para cada combinação de pares de variáveis numéricas no conjunto de dados.

Poderíamos criar este tipo de matriz para visualizar simultaneamente a relação entre tamanho do agregado familiar, rendimento anual e número de animais de estimação.

Recurso : Confira este tutorial para ver como criar uma matriz de gráfico de dispersão em R.

Outra forma de realizar análises multivariadas neste conjunto de dados seria ajustar um modelo de regressão linear múltipla . Por exemplo, poderíamos criar um modelo de regressão que utilizasse o tamanho da família e o número de animais de estimação para prever a renda anual.

Recurso : Confira este tutorial para ver como realizar regressão linear múltipla em R.

Outra forma de realizar análise multivariada neste conjunto de dados seria realizar análise de componentes principais , o que nos permite encontrar a estrutura subjacente no conjunto de dados.

Recurso : Confira este tutorial para ver como realizar a análise de componentes principais em R.

Conclusão

Aqui está um breve resumo deste artigo:

• A análise univariada é a análise de uma variável.
• A análise multivariada é a análise de mais de uma variável.
• Existem diferentes maneiras de realizar cada tipo de análise dependendo do seu objetivo final.
• No mundo real, frequentemente realizamos os dois tipos de análise em um único conjunto de dados.
• A análise univariada nos permite compreender a distribuição de valores de uma variável, enquanto a análise multivariada nos permite compreender a relação entre múltiplas variáveis.