Anova vs regressão: qual a diferença?

Dois modelos comumente usados em estatística são ANOVA e modelos de regressão.

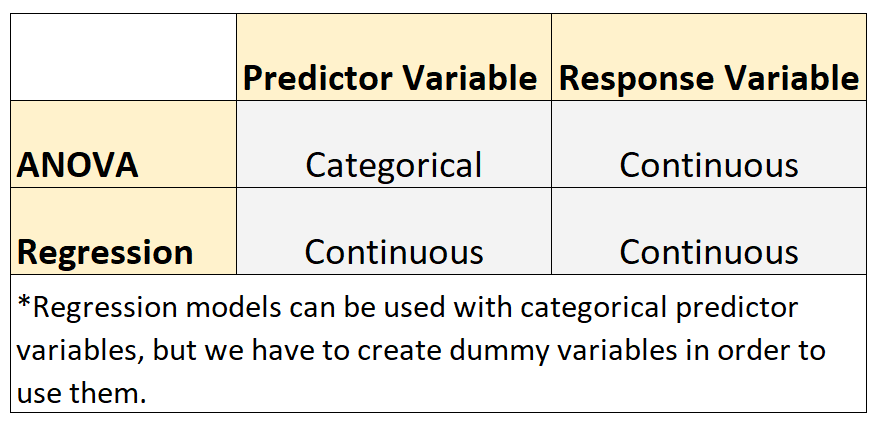
Esses dois tipos de modelos compartilham a seguinte semelhança:

• A variável resposta em cada modelo é contínua. Exemplos de variáveis contínuas incluem peso, altura, comprimento, largura, tempo, idade, etc.

No entanto, esses dois tipos de modelos compartilham a seguinte diferença :

• Os modelos ANOVA são usados quando as variáveis preditoras são categóricas. Exemplos de variáveis categóricas incluem nível de escolaridade, cor dos olhos, estado civil, etc.
• Modelos de regressão são usados quando as variáveis preditoras são contínuas.*

*Modelos de regressão podem ser usados com variáveis preditoras categóricas, mas precisamos criar variáveis fictícias para usá-las.

Os exemplos a seguir mostram quando usar ANOVA ou modelos de regressão na prática.

Exemplo 1: Modelo ANOVA preferido

Suponha que um biólogo queira entender se quatro fertilizantes diferentes levam ou não ao mesmo crescimento médio das plantas (em polegadas) durante o período de um mês. Para testar isso, ela aplica cada fertilizante em 20 plantas e registra o crescimento de cada planta após um mês.

Nesse cenário, o biólogo deve utilizar um modelo ANOVA unidirecional para analisar as diferenças entre os fertilizantes porque existe uma variável preditora e ela é categórica.

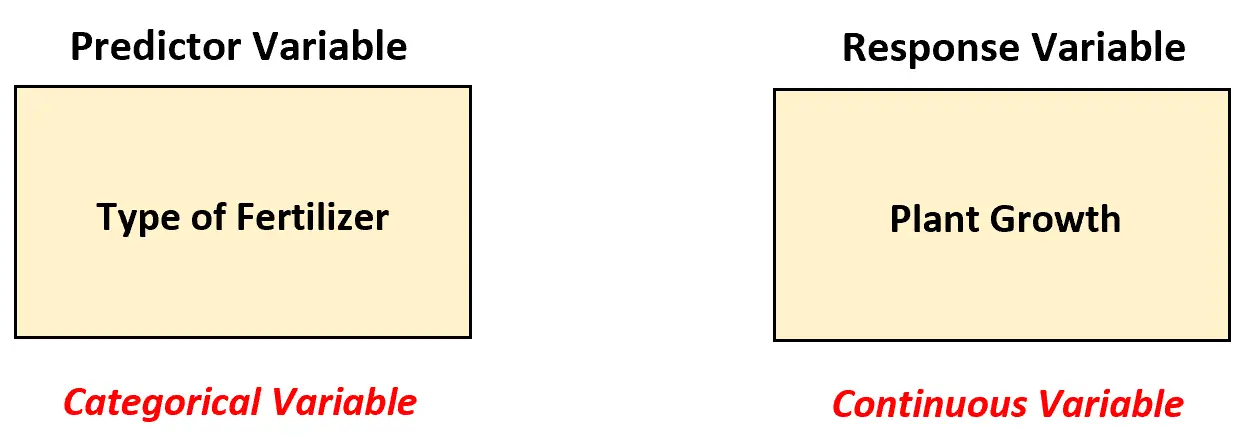
Em outras palavras, os valores da variável preditora podem ser classificados nas seguintes “categorias”:

• Fertilizante 1
• Fertilizante 2
• Fertilizante 3
• Fertilizante 4

Uma ANOVA unidirecional dirá ao biólogo se o crescimento médio das plantas é ou não igual entre os quatro fertilizantes diferentes.

Exemplo 2: Modelo de Regressão Preferencial

Digamos que um corretor de imóveis queira entender a relação entre a metragem quadrada e o preço do imóvel. Para analisar essa relação, ele coleta dados sobre a metragem quadrada e o preço de 200 casas em uma determinada cidade.

Nesse cenário, o agente imobiliário deve utilizar um modelo de regressão linear simples para analisar a relação entre essas duas variáveis, pois a variável preditora (metragem quadrada) é contínua.

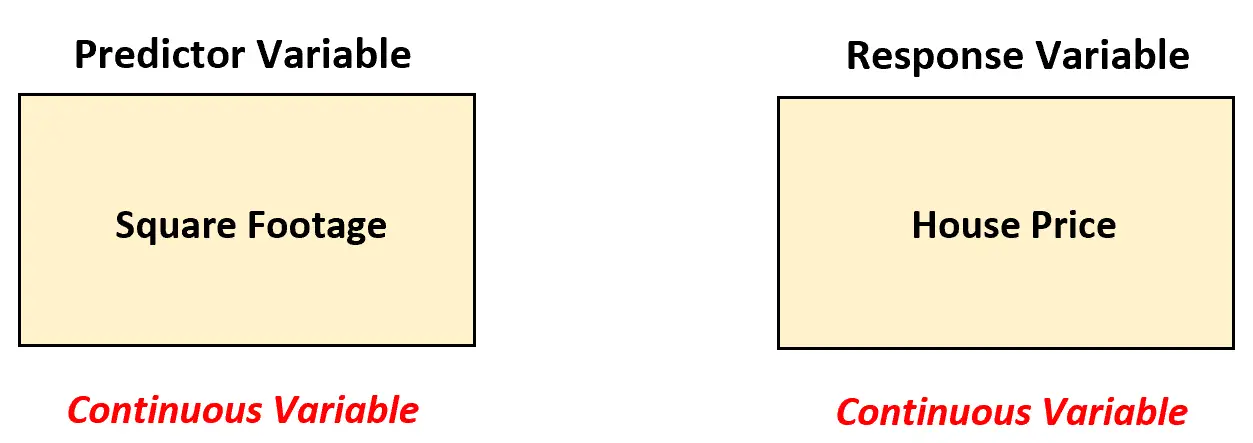
Utilizando regressão linear simples, o agente imobiliário pode ajustar o seguinte modelo de regressão:

Preço do imóvel = β ₀ + β ₁ (área quadrada)

O valor de β ₁ representará a variação média no preço da habitação associada a cada metro quadrado adicional.

Isso permitirá ao agente imobiliário quantificar a relação entre a metragem quadrada e o preço do imóvel.

Exemplo 3: Modelo de regressão com variáveis dummy preferenciais

Suponha que um corretor de imóveis queira entender a relação entre as variáveis preditoras “metragem quadrada” e “tipo de casa” (unifamiliar, apartamento, sobrado) com a variável resposta preço do imóvel.

Neste cenário, o agente imobiliário pode utilizar a regressão linear múltipla convertendo o “tipo de casa” em uma variável dummy, uma vez que atualmente é uma variável categórica.

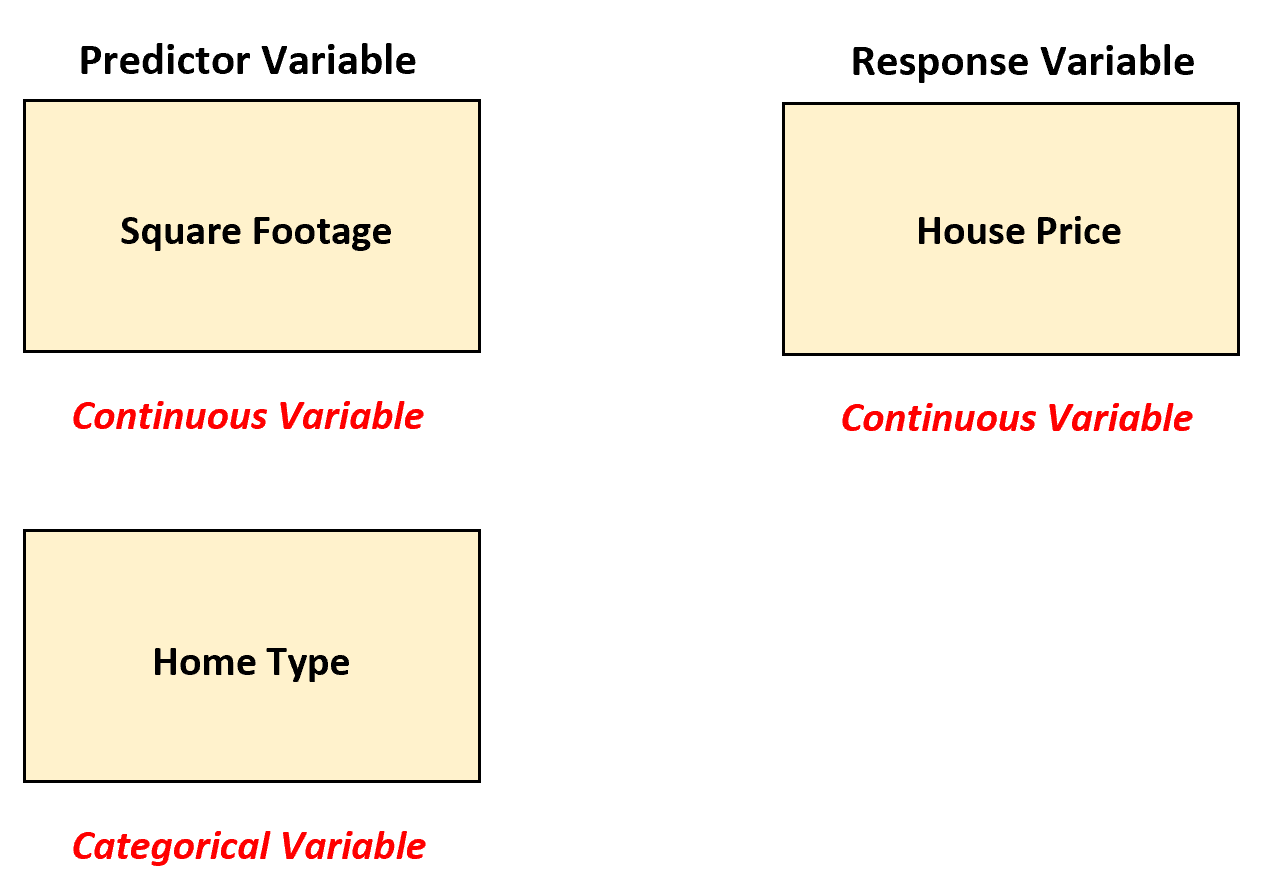
O agente imobiliário pode então ajustar o seguinte modelo de regressão linear múltipla:

Preço do imóvel = β ₀ + β ₁ (área quadrada) + β ₂ (família unifamiliar) + β ₃ (apartamento)

Aqui está como interpretaríamos os coeficientes do modelo:

• β ₁ : A variação média no preço da habitação associada a um metro quadrado adicional.
• β ₂ : A diferença média de preço entre uma casa unifamiliar e uma casa geminada, assumindo que a metragem quadrada permanece constante.
• β ₃ : Diferença média de preço entre uma casa unifamiliar e um apartamento, assumindo uma superfície constante.

Confira os seguintes tutoriais para ver como criar variáveis fictícias em diferentes softwares estatísticos:

• Como criar variáveis fictícias em R
• Como criar variáveis fictícias no Excel

Recursos adicionais

Os tutoriais a seguir fornecem uma introdução detalhada aos modelos ANOVA:

• Introdução à ANOVA unidirecional
• Introdução à ANOVA bidirecional

Os tutoriais a seguir fornecem uma introdução detalhada aos modelos de regressão linear:

• Introdução à regressão linear simples
• Introdução à regressão linear múltipla