Binompdf vs binomcdf: a diferença (mais exemplos)

A distribuição binomial é uma das distribuições mais comumente usadas em todas as estatísticas.

Em uma calculadora TI-84, você pode usar duas funções para encontrar probabilidades relacionadas à distribuição binomial:

• binompdf(n, p, x) : encontra a probabilidade de que exatamente x sucessos ocorram ao longo de n tentativas, onde a probabilidade de sucesso em uma determinada tentativa é igual a p .
• binomcdf(n, p, x) : encontra a probabilidade de que x ou menos sucessos ocorram em n tentativas, onde a probabilidade de sucesso em uma determinada tentativa é igual a p .

Você pode acessar cada uma dessas funções em uma calculadora TI-84 pressionando 2 e depois VARS . Isso o levará a uma tela DISTR onde você poderá usar binompdf() e binomcdf() :

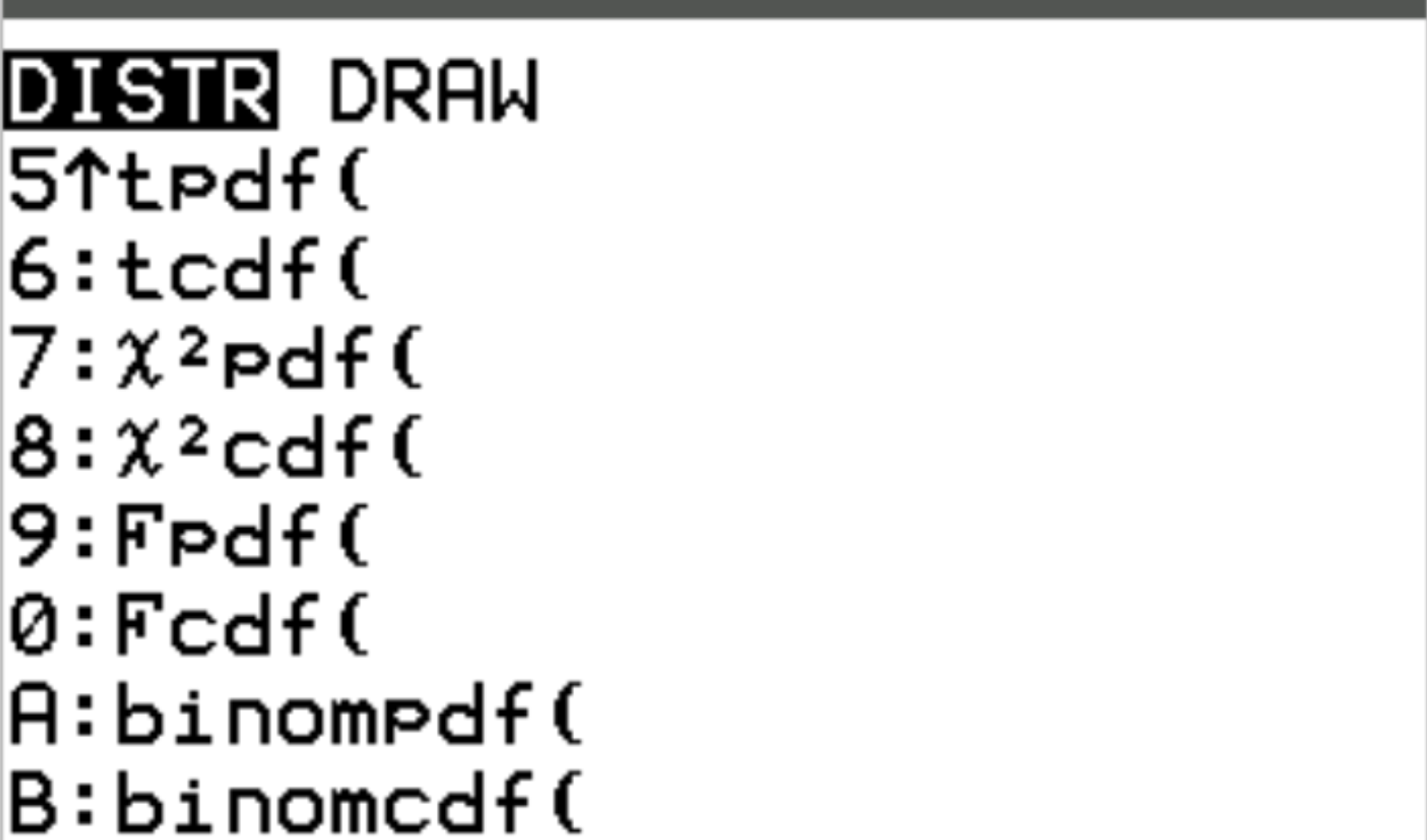
Os exemplos a seguir mostram como usar cada uma dessas funções na prática.

Exemplos: Como usar Binompdf()

Os exemplos a seguir mostram como usar a função binompdf() .

Exemplo 1: Tentativas de lance livre

Jéssica acerta 80% de suas tentativas de lance livre. Se ela acertar 10 lances livres, qual é a probabilidade de ela acertar exatamente 7?

Para responder a esta pergunta, podemos digitar a seguinte fórmula:

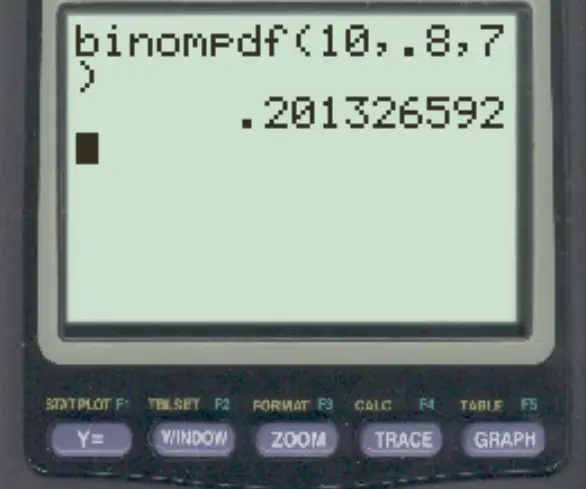
A probabilidade de ela obter exatamente 7 é 0,2013 .

Exemplo 2: transações fraudulentas

Um banco sabe que 3% de todas as transações são fraudulentas. Se ocorrerem 20 transações em um determinado dia, qual é a probabilidade de que exatamente 2 sejam fraudulentas?

Para responder a esta pergunta, podemos digitar a seguinte fórmula:

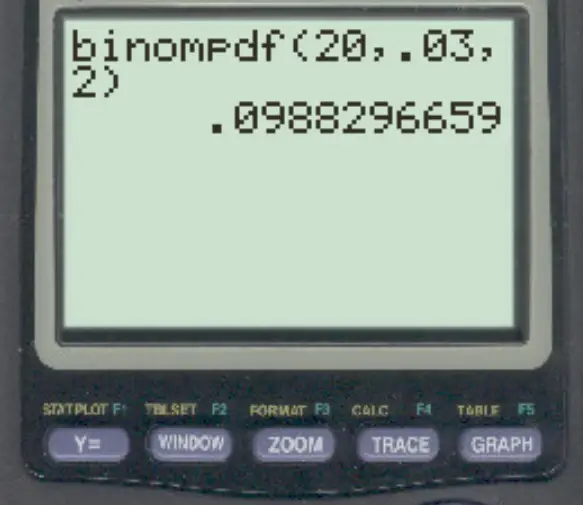
A probabilidade de que exatamente 2 transações sejam fraudulentas é de 0,0988 .

Exemplos: Como usar Binomcdf()

Os exemplos a seguir mostram como usar a função binomcdf() .

Exemplo 1: Tentativas de lance livre

Jéssica acerta 50% de suas tentativas de lance livre. Se ela acertar 10 lances livres, qual é a probabilidade de ela acertar 7 ou menos?

Para responder a esta pergunta, podemos digitar a seguinte fórmula:

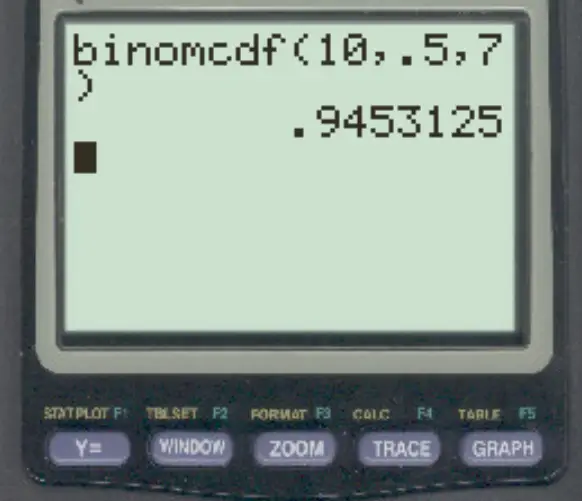
A probabilidade de ela acertar 7 ou menos lances livres é 0,9453 .

Exemplo 2: transações fraudulentas

Um banco sabe que 3% de todas as transações são fraudulentas. Se ocorrerem 20 transações em um determinado dia, qual é a probabilidade de que mais de 2 transações sejam fraudulentas?

Para responder a esta pergunta, podemos digitar a seguinte fórmula:

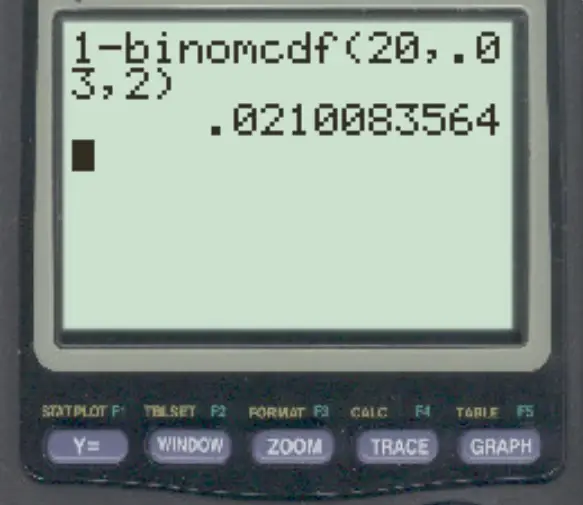
A probabilidade de mais de 2 transações serem fraudulentas é de 0,021 .

Recursos adicionais

Calculadora de distribuição binomial
Como realizar um teste binomial no Excel