Como criar florestas aleatórias em r (passo a passo)

Quando a relação entre um conjunto de variáveis preditoras e uma variável de resposta é muito complexa, frequentemente usamos métodos não lineares para modelar a relação entre elas.

Um desses métodos é construir uma árvore de decisão . No entanto, a desvantagem de usar uma única árvore de decisão é que ela tende a sofrer de alta variância .

Ou seja, se dividirmos o conjunto de dados em duas metades e aplicarmos a árvore de decisão a ambas as metades, os resultados poderão ser muito diferentes.

Um método que podemos usar para reduzir a variância de uma única árvore de decisão é construir um modelo de floresta aleatório , que funciona da seguinte forma:

1. Pegue b amostras inicializadas do conjunto de dados original.

2. Crie uma árvore de decisão para cada amostra de bootstrap.

• Ao construir a árvore, cada vez que uma divisão é considerada, apenas uma amostra aleatória de m preditores é considerada candidata à divisão do conjunto completo de p preditores. Geralmente, escolhemos m igual a √p .

3. Calcule a média das previsões de cada árvore para obter um modelo final.

Acontece que florestas aleatórias tendem a produzir modelos muito mais precisos do que árvores de decisão única e até mesmo modelos empacotados .

Este tutorial fornece um exemplo passo a passo de como criar um modelo de floresta aleatório para um conjunto de dados em R.

Passo 1: Carregue os pacotes necessários

Primeiro, carregaremos os pacotes necessários para este exemplo. Para este exemplo simples, precisamos apenas de um pacote:

 library (randomForest)

Etapa 2: ajustar o modelo de floresta aleatória

Para este exemplo, usaremos um conjunto de dados R integrado chamado Qualidade do Ar , que contém medições da qualidade do ar na cidade de Nova York durante 153 dias individuais.

 #view structure of air quality dataset
str(airquality)

'data.frame': 153 obs. of 6 variables:
 $ Ozone: int 41 36 12 18 NA 28 23 19 8 NA ...
 $Solar.R: int 190 118 149 313 NA NA 299 99 19 194 ...
 $ Wind: num 7.4 8 12.6 11.5 14.3 14.9 8.6 13.8 20.1 8.6 ...
 $ Temp: int 67 72 74 62 56 66 65 59 61 69 ...
 $Month: int 5 5 5 5 5 5 5 5 5 5 ...
 $Day: int 1 2 3 4 5 6 7 8 9 10 ...

#find number of rows with missing values
sum(! complete . cases (airquality))

[1] 42

Este conjunto de dados possui 42 linhas com valores ausentes. Portanto, antes de ajustar um modelo de floresta aleatório, preencheremos os valores faltantes em cada coluna com as medianas das colunas:

 #replace NAs with column medians
for (i in 1: ncol (air quality)) {
  airquality[,i][ is . na (airquality[, i])] <- median (airquality[, i], na . rm = TRUE )
}

Relacionado: Como imputar valores ausentes em R

O código a seguir mostra como ajustar um modelo de floresta aleatório em R usando a função randomForest() do pacote randomForest .

 #make this example reproducible
set.seed(1)

#fit the random forest model
model <- randomForest(
  formula = Ozone ~ .,
  data = airquality
)

#display fitted model
model

Call:
 randomForest(formula = Ozone ~ ., data = airquality) 
               Type of random forest: regression
                     Number of trees: 500
No. of variables tried at each split: 1

          Mean of squared residuals: 327.0914
                    % Var explained: 61

#find number of trees that produce lowest test MSE
which.min(model$mse)

[1] 82

#find RMSE of best model
sqrt(model$mse[ which . min (model$mse)]) 

[1] 17.64392

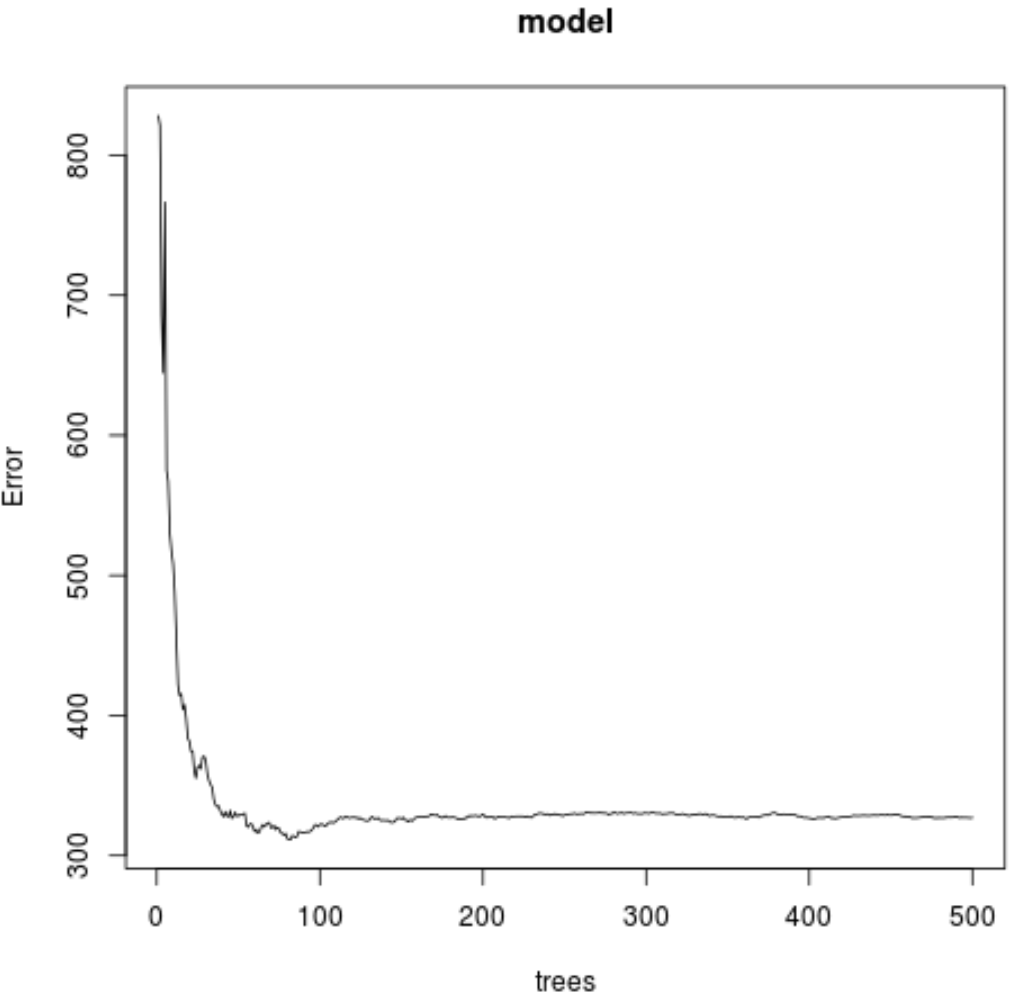
Pelo resultado, podemos perceber que o modelo que produziu o menor erro quadrático médio (MSE) de teste utilizou 82 árvores.

Também podemos ver que a raiz do erro quadrático médio deste modelo foi 17,64392 . Podemos pensar nisso como a diferença média entre o valor previsto para o ozônio e o valor real observado.

Também podemos usar o código a seguir para produzir um gráfico do teste MSE com base no número de árvores usadas:

 #plot the MSE test by number of trees
plot(model)

E podemos usar a função varImpPlot() para criar um gráfico que exibe a importância de cada variável preditora no modelo final:

 #produce variable importance plot
varImpPlot(model) 

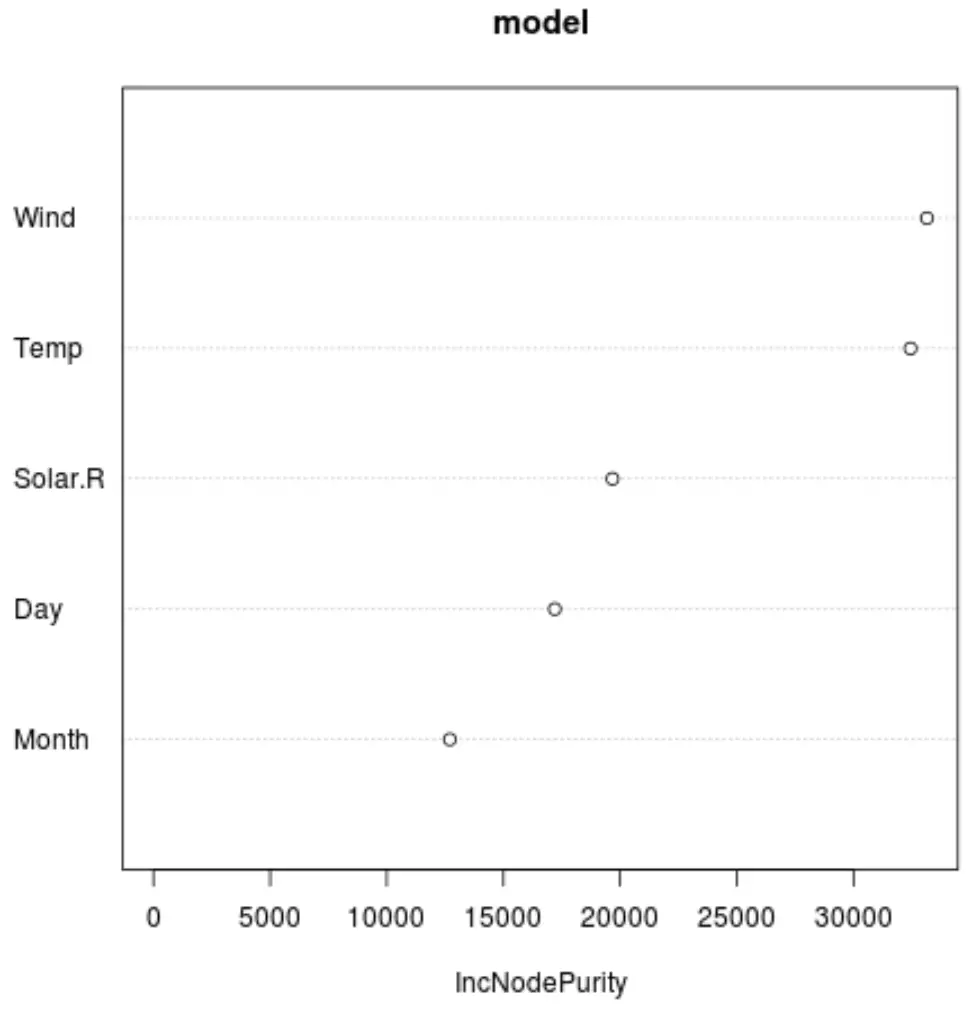
O eixo x exibe o aumento médio na pureza dos nós das árvores de regressão como uma função da divisão entre os diferentes preditores exibidos no eixo y.

No gráfico, podemos ver que Vento é a variável preditora mais importante, seguida de perto por Temp .

Etapa 3: ajuste o modelo

Por padrão, a função randomForest() usa 500 árvores e (total de preditores/3) preditores selecionados aleatoriamente como candidatos potenciais para cada divisão. Podemos ajustar esses parâmetros usando a função tuneRF() .

O código a seguir mostra como encontrar o modelo ideal usando as seguintes especificações:

• ntreeTry: O número de árvores a serem construídas.
• mtryStart: o número inicial de variáveis preditoras a serem consideradas em cada divisão.
• stepFactor: Fator para aumentar até que o erro fora da sacola estimado pare de melhorar em um determinado valor.
• melhorar: a quantidade pela qual o erro de saída da bolsa deve ser melhorado para continuar aumentando o fator de passo.

 model_tuned <- tuneRF(
               x=airquality[,-1], #define predictor variables
               y=airquality$Ozone, #define response variable
               ntreeTry= 500 ,
               mtryStart= 4 , 
               stepFactor= 1.5 ,
               improve= 0.01 ,
               trace= FALSE #don't show real-time progress
               )

Esta função produz o gráfico a seguir, que exibe o número de preditores usados em cada divisão ao construir as árvores no eixo x e o erro fora do saco estimado no eixo y:

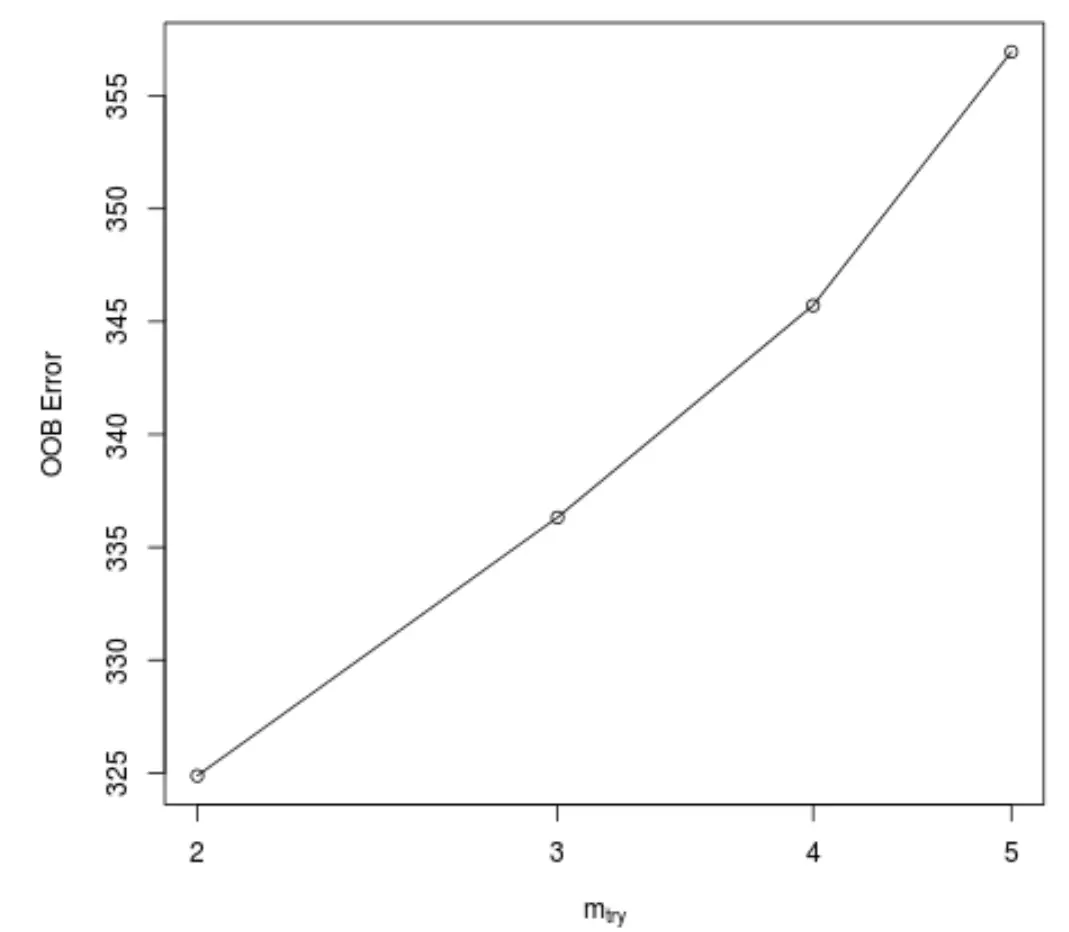
Podemos ver que o menor erro OOB é obtido usando 2 preditores escolhidos aleatoriamente em cada divisão ao construir as árvores.

Na verdade, isso corresponde à configuração padrão (total de preditores/3 = 6/3 = 2) usada pela função randomForest() inicial.

Etapa 4: use o modelo final para fazer previsões

Finalmente, podemos usar o modelo de floresta aleatória ajustado para fazer previsões sobre novas observações.

 #define new observation
new <- data.frame(Solar.R=150, Wind=8, Temp=70, Month=5, Day=5)

#use fitted bagged model to predict Ozone value of new observation
predict(model, newdata=new)

27.19442

Com base nos valores das variáveis preditoras, o modelo de floresta aleatória ajustado prevê que o valor do ozônio será 27,19442 neste dia específico.

O código R completo usado neste exemplo pode ser encontrado aqui .