Como calcular um coeficiente de correlação em uma calculadora ti-84
Um coeficiente de correlação é uma medida da associação linear entre duas variáveis. Pode assumir um valor entre -1 e 1 onde:
- -1 indica uma correlação linear perfeitamente negativa entre duas variáveis
- 0 indica nenhuma correlação linear entre duas variáveis
- 1 indica uma correlação linear perfeitamente positiva entre duas variáveis
Você pode usar as seguintes etapas para calcular o coeficiente de correlação entre duas variáveis em uma calculadora TI-84:
Etapa 1: Habilite o diagnóstico.
Primeiro, precisamos habilitar o diagnóstico. Para fazer isso, pressione 2 e depois pressione o número 0. Isso nos levará para a tela CATALOG.

Vá até DiagnosticOn e pressione ENTER .
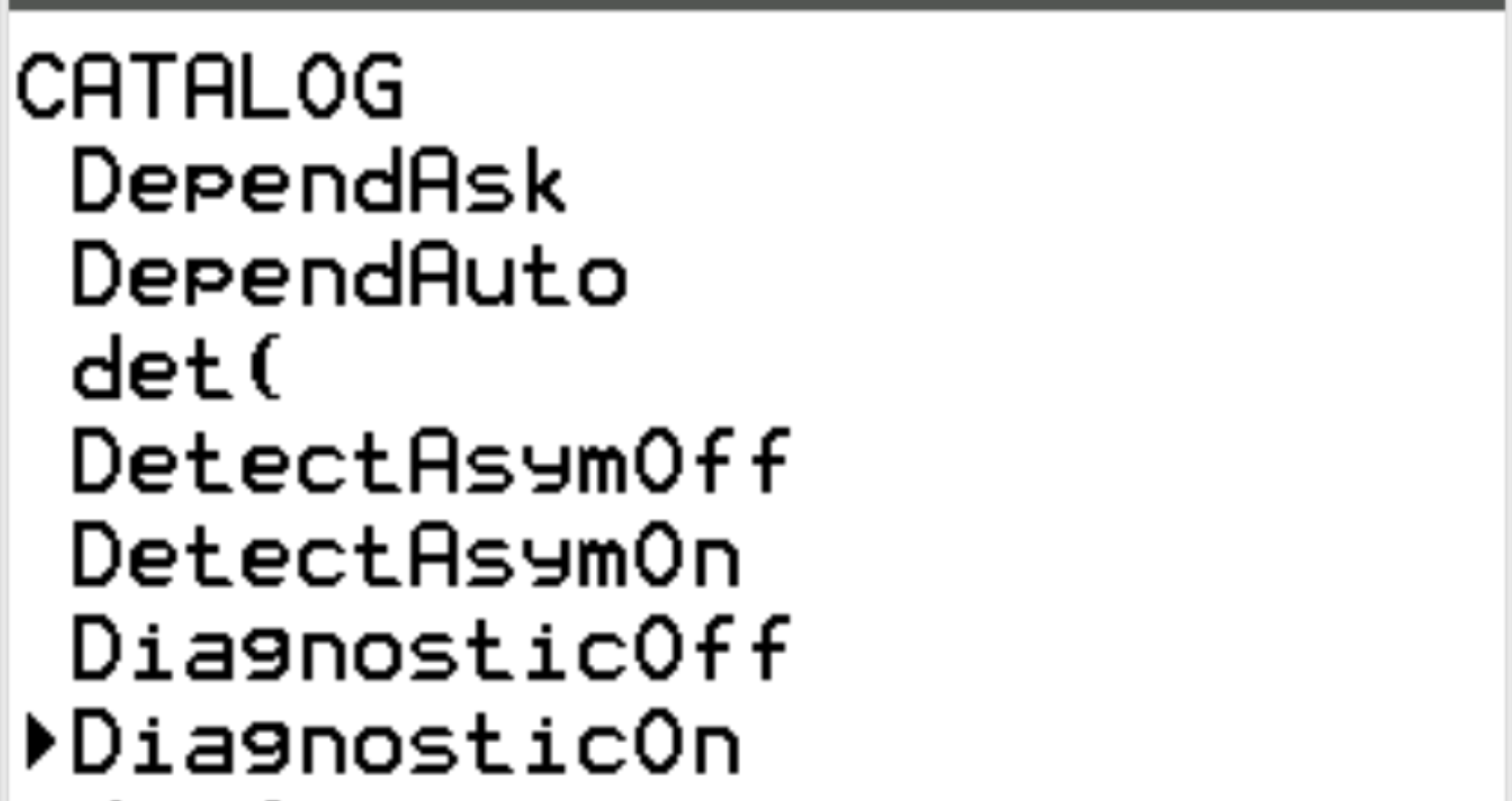
Em seguida, pressione ENTER novamente.
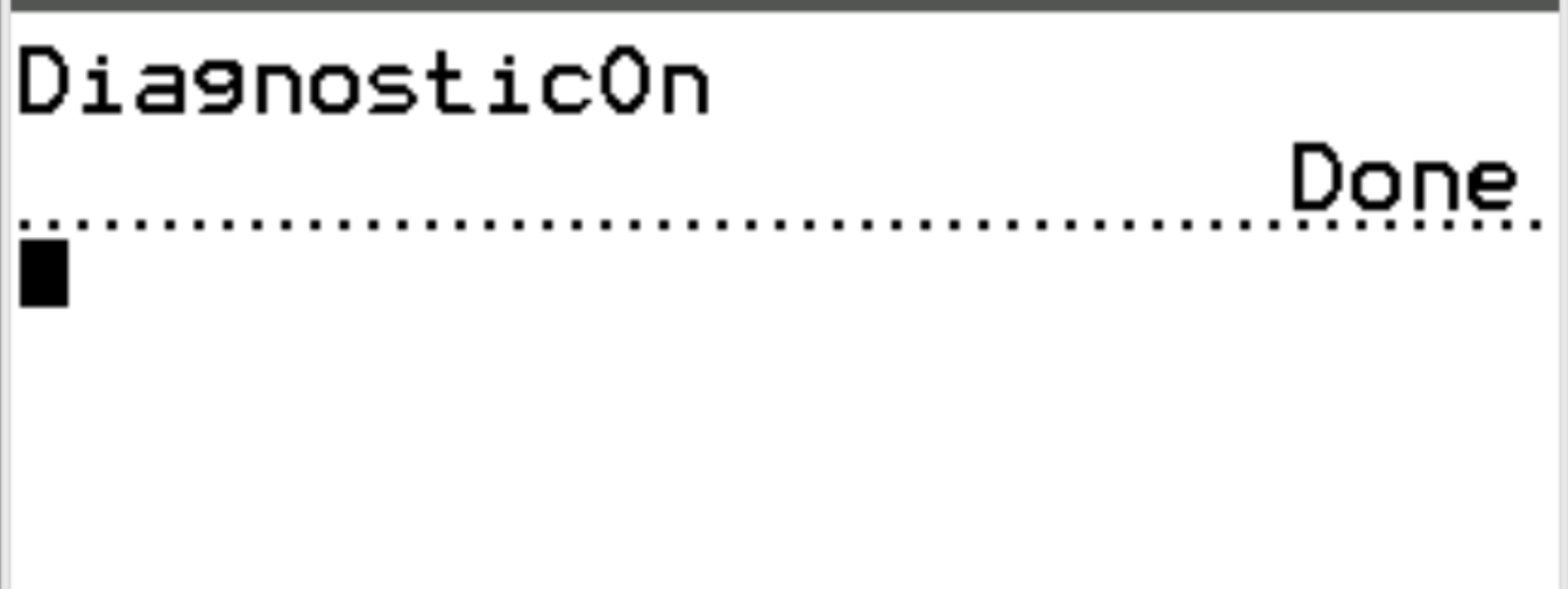
Os diagnósticos agora estão habilitados para que possamos calcular o coeficiente de correlação entre duas variáveis.
Passo 2: Insira os dados.
A seguir, precisamos inserir os valores dos dados para nossas duas variáveis. Pressione Stat e depois pressione EDIT . Insira os valores da primeira variável na coluna L1 e os valores da segunda variável na coluna L2:
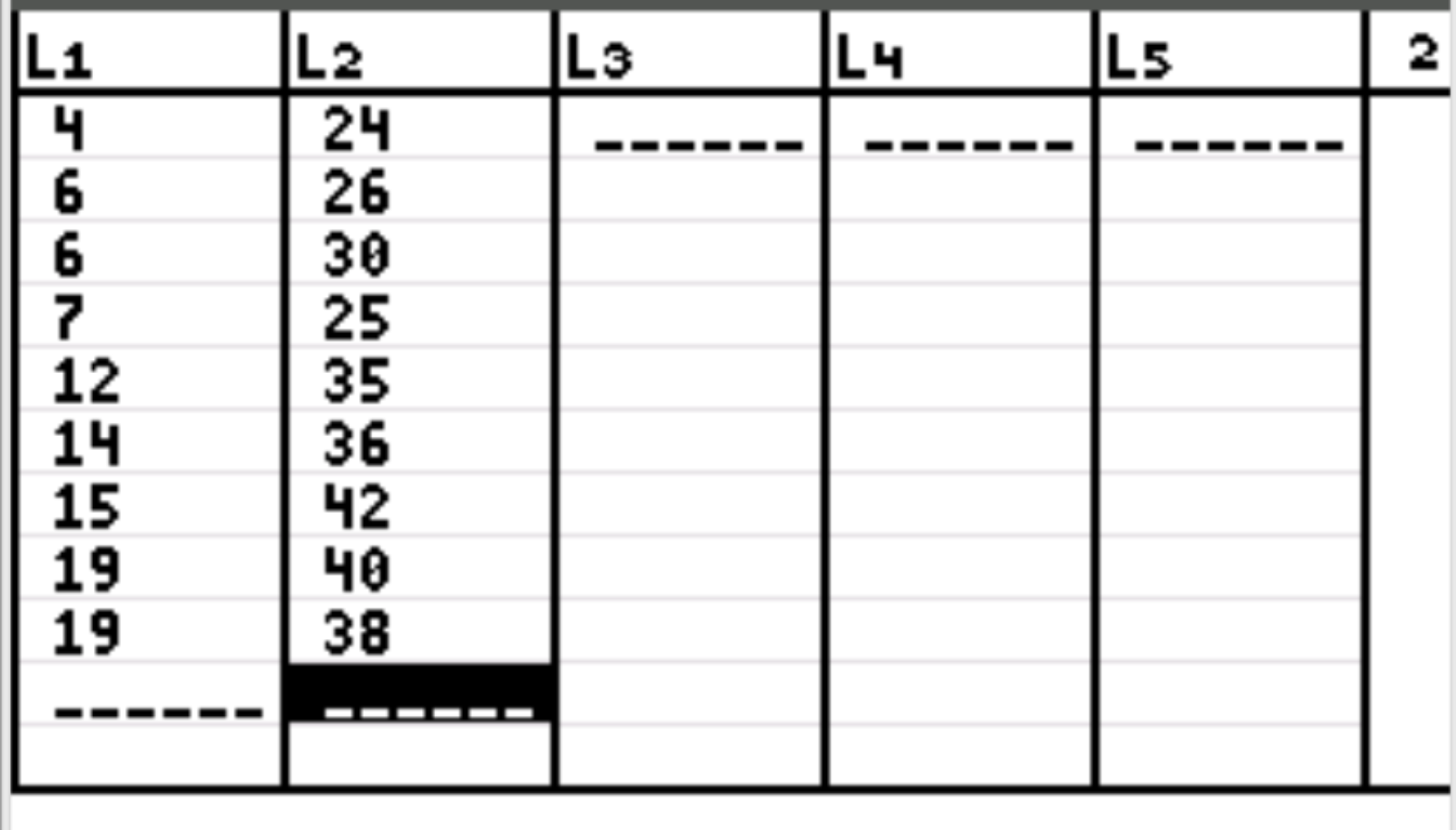
Etapa 3: Encontre o coeficiente de correlação.
A seguir, calcularemos o coeficiente de correlação entre as duas variáveis. Pressione Stat e vá até CALC . Em seguida, vá até 8: Linreg(a+bx) e pressione Enter .
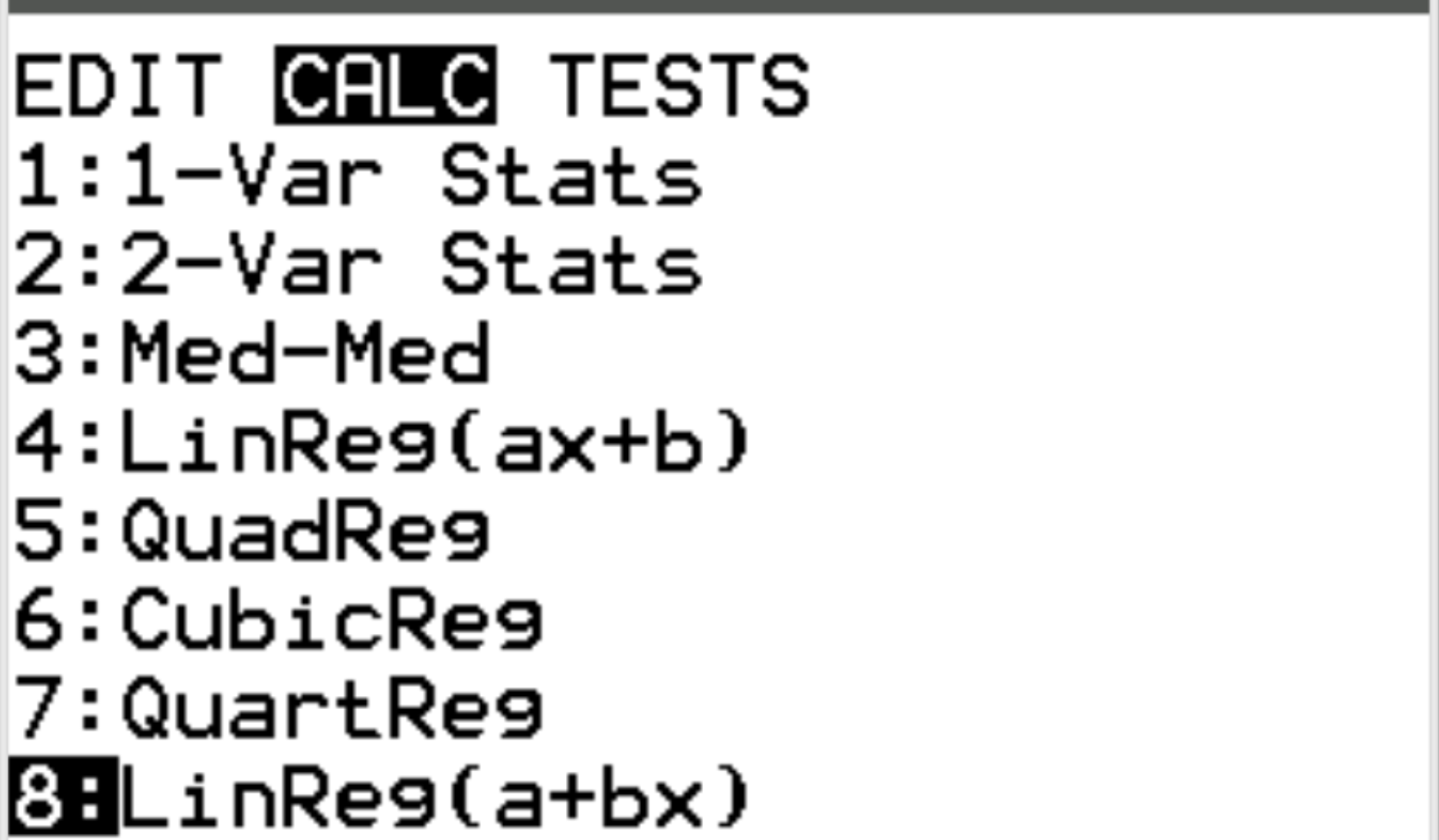
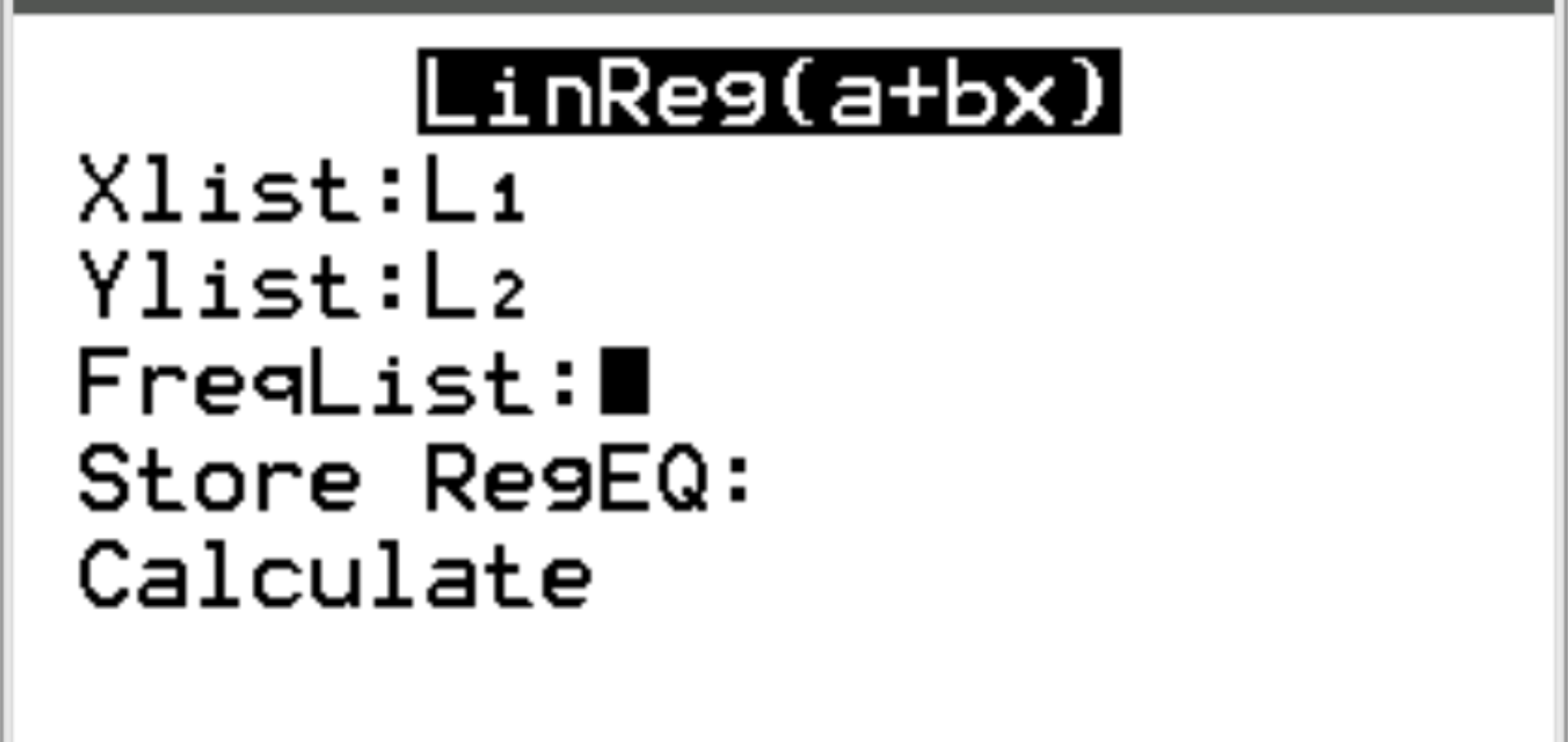
Para Xlist e Ylist, certifique-se de que L1 e L2 estejam selecionados, pois essas são as colunas que usamos para inserir nossos dados. Deixe FreqList vazio. Role para baixo até Calcular e pressione Enter .
Na nova tela podemos ver que o coeficiente de correlação (r) entre as duas variáveis é 0,9145 .
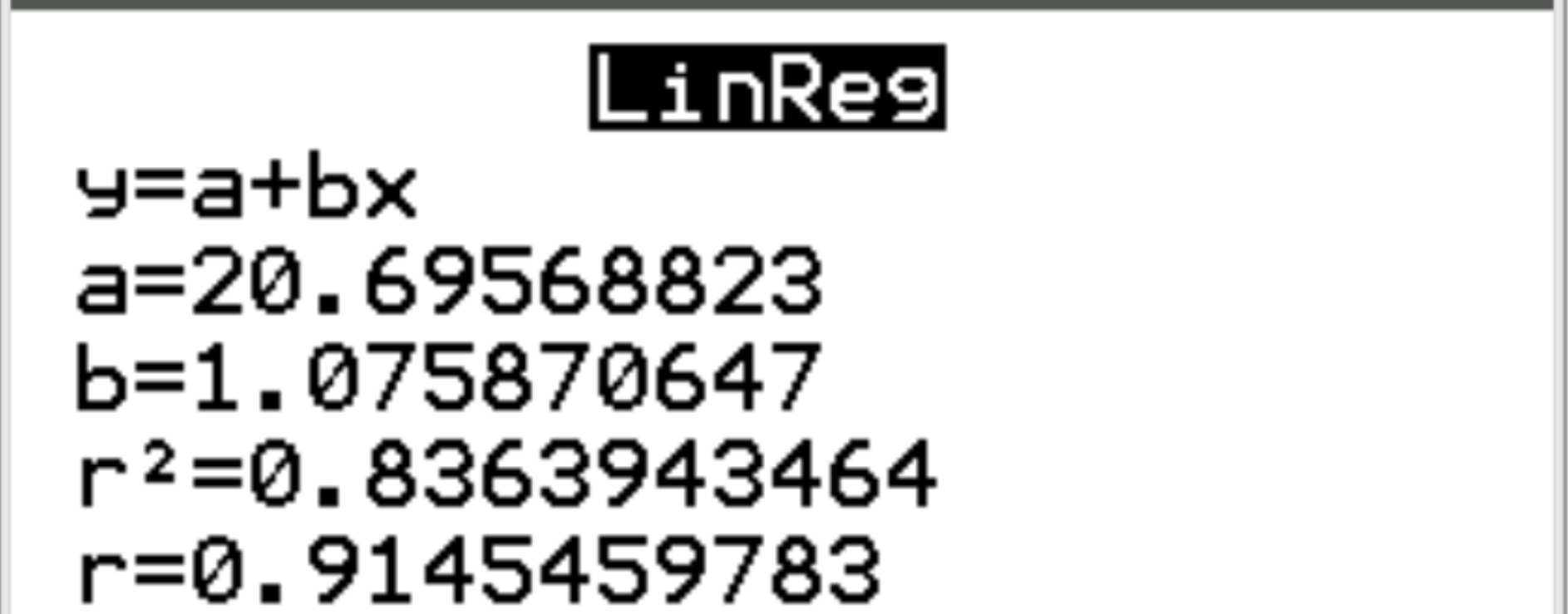
Como interpretar um coeficiente de correlação
A tabela a seguir mostra a regra prática para interpretar a força do relacionamento entre duas variáveis com base no valor de r :
| Valor absoluto de r | Força do relacionamento |
|---|---|
| r < 0,25 | Sem relacionamento |
| 0,25 < r < 0,5 | Relacionamento fraco |
| 0,5 < r < 0,75 | Relacionamentos moderados |
| r > 0,75 | Relacionamentos fortes |
No nosso exemplo, um coeficiente de correlação de 0,9145 indica uma forte relação positiva entre as duas variáveis.