Como calcular probabilidades normais em uma calculadora ti-84

A distribuição normal é a distribuição mais comumente usada em todas as estatísticas. Este tutorial explica como usar as seguintes funções em uma calculadora TI-84 para encontrar probabilidades de distribuição normal:

normalpdf(x, μ, σ) retorna a probabilidade associada à pdf normal onde:

• x = valor individual
• μ = média populacional
• σ = desvio padrão populacional

normalcdf(lower_x, upper_x, μ, σ) retorna a probabilidade cumulativa associada ao cdf normal entre dois valores.

Ouro:

• lower_x = menor valor individual
• superior_x = valor individual superior
• μ = média populacional
• σ = desvio padrão populacional

Essas duas funções são acessíveis em uma calculadora TI-84 pressionando 2nd e depois pressionando vars . Isso o levará a uma tela DISTR onde você poderá usar normalpdf() e normalcdf() :

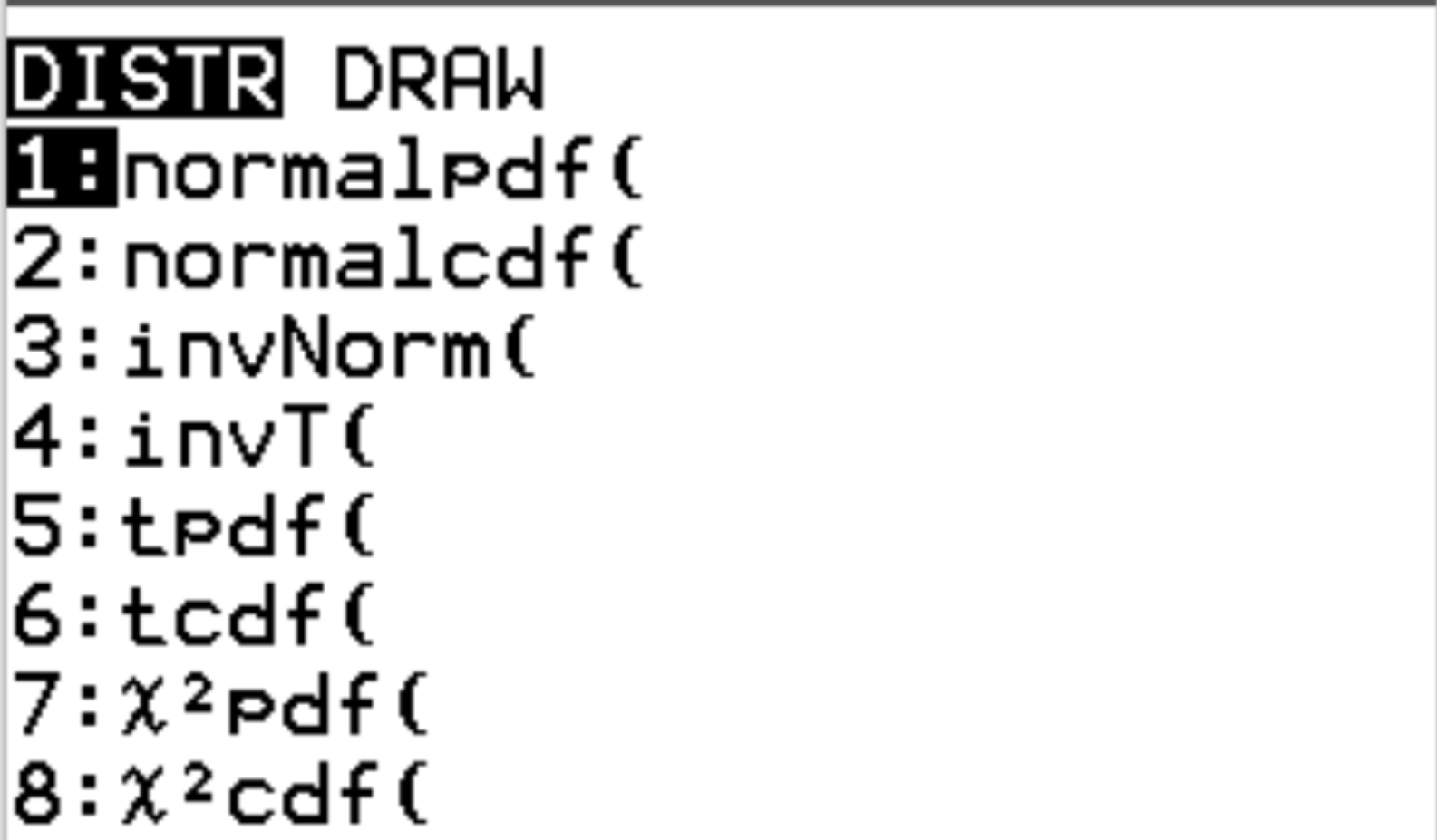
Os exemplos a seguir ilustram como usar essas funções para responder a diferentes perguntas.

Exemplo 1: probabilidade normal maior que x

Pergunta: Para uma distribuição normal com média = 40 e desvio padrão = 6, encontre a probabilidade de um valor ser maior que 45.

Resposta: Use a função normalcdf(x, 10000, μ, σ):

normalcdf(45, 10000, 40, 6) = 0,2023

Nota: Como a função requer um valor upper_x, simplesmente usamos 10.000.

Exemplo 2: probabilidade normal menor que x

Pergunta: Para uma distribuição normal com média = 100 e desvio padrão = 11,3, encontre a probabilidade de um valor ser inferior a 98.

Resposta: Use a função normalcdf(-10000, x, μ, σ):

normalcdf(-10000, 98, 100, 11,3) = 0,4298

Nota: Como a função requer um valor lower_x, simplesmente usamos -10000.

Exemplo 3: Probabilidade normal entre dois valores

Pergunta: Para uma distribuição normal com média = 50 e desvio padrão = 4, encontre a probabilidade de um valor estar entre 48 e 52.

Resposta: Use a função normalcdf(smaller_x, Larger_x, μ, σ)

normalcdf(48, 52, 50, 4) = 0,3829

Exemplo 4: Probabilidade normal separada de dois valores

Pergunta: Para uma distribuição normal com média = 22 e desvio padrão = 4, encontre a probabilidade de um valor ser menor que 20 ou maior que 24.

Resposta: Use a função normalcdf(-10000, small_x, μ, σ) + normalcdf(larger_x, 10000, μ, σ)

normalcdf(-10000, 20, 22, 4) + normalcdf(24, 10000, 22, 4) = 0,6171