Teste de ajuste qui-quadrado em uma calculadora ti-84

Um teste de ajuste qui-quadrado é usado para determinar se uma variável categórica segue ou não uma distribuição hipotética.

Este tutorial explica como realizar um teste de ajuste qui-quadrado em uma calculadora TI-84.

Exemplo: teste de ajuste qui-quadrado em uma calculadora TI-84

O dono de uma loja diz que um número igual de clientes vem à sua loja todos os dias da semana. Para testar esta hipótese, um investigador independente regista o número de clientes que entram na loja numa determinada semana e descobre o seguinte:

• Segunda-feira: 50 clientes
• Terça-feira: 60 clientes
• Quarta-feira: 40 clientes
• Quinta-feira: 47 clientes
• Sexta-feira: 53 clientes

Usaremos as etapas a seguir para realizar um teste de adequação do qui-quadrado para determinar se os dados são consistentes com a afirmação do proprietário da loja.

Passo 1: Insira os dados.

Primeiro, inseriremos os valores dos dados para o número esperado de clientes por dia e o número observado de clientes por dia. Pressione Stat e depois pressione EDIT . Insira os seguintes valores para o número observado de clientes na coluna L1 e os valores para o número esperado de clientes na coluna L2:

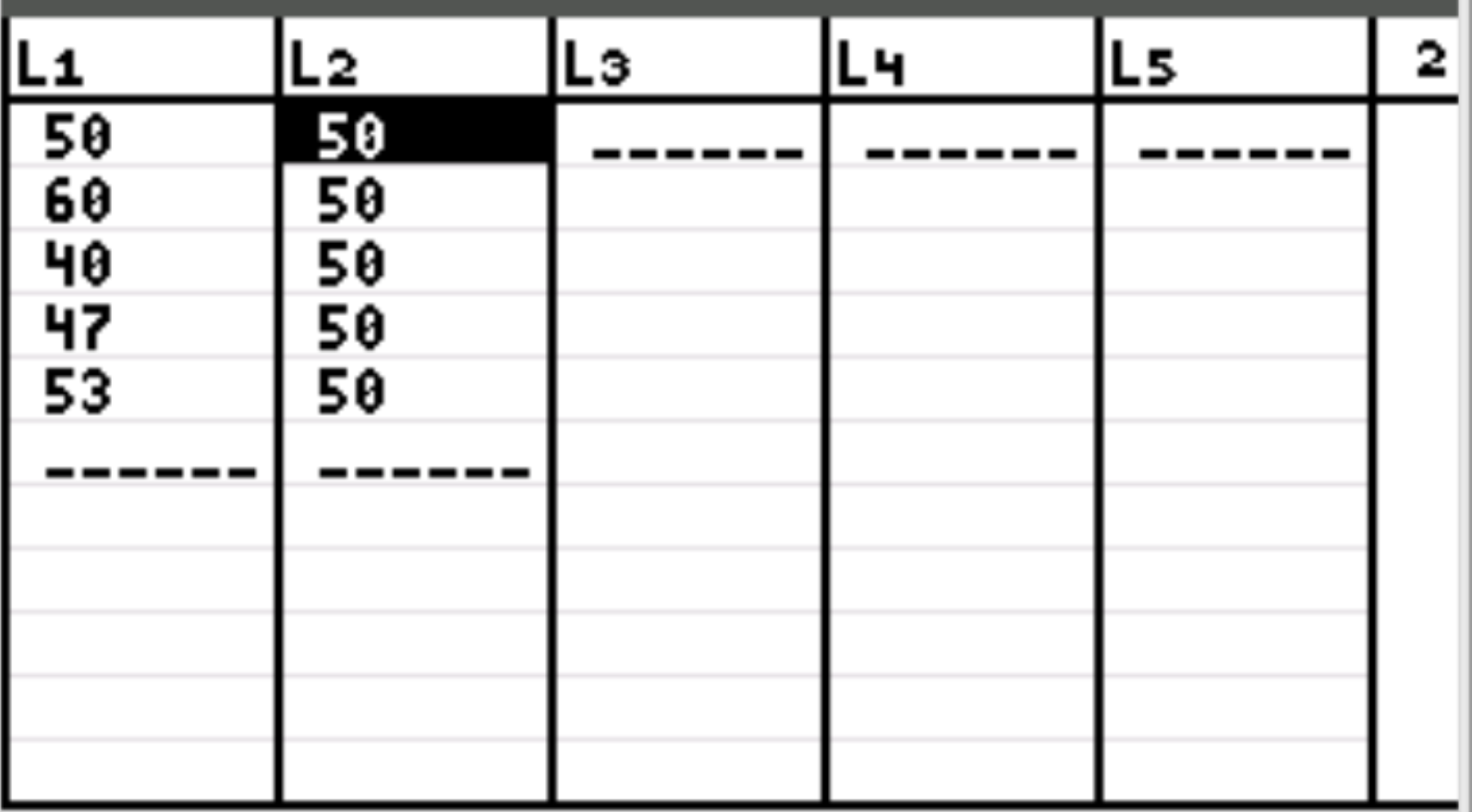
Nota: Havia 250 clientes no total. Portanto, se o dono da loja espera que um número igual de clientes entre na loja todos os dias, seriam 50 clientes por dia.

Etapa 2: execute o teste de adequação do qui-quadrado.

A seguir, realizaremos o teste de adequação do qui-quadrado. Pressione Stat e vá até TESTES . Em seguida, role para baixo até X ² GOF-Test e pressione Enter .

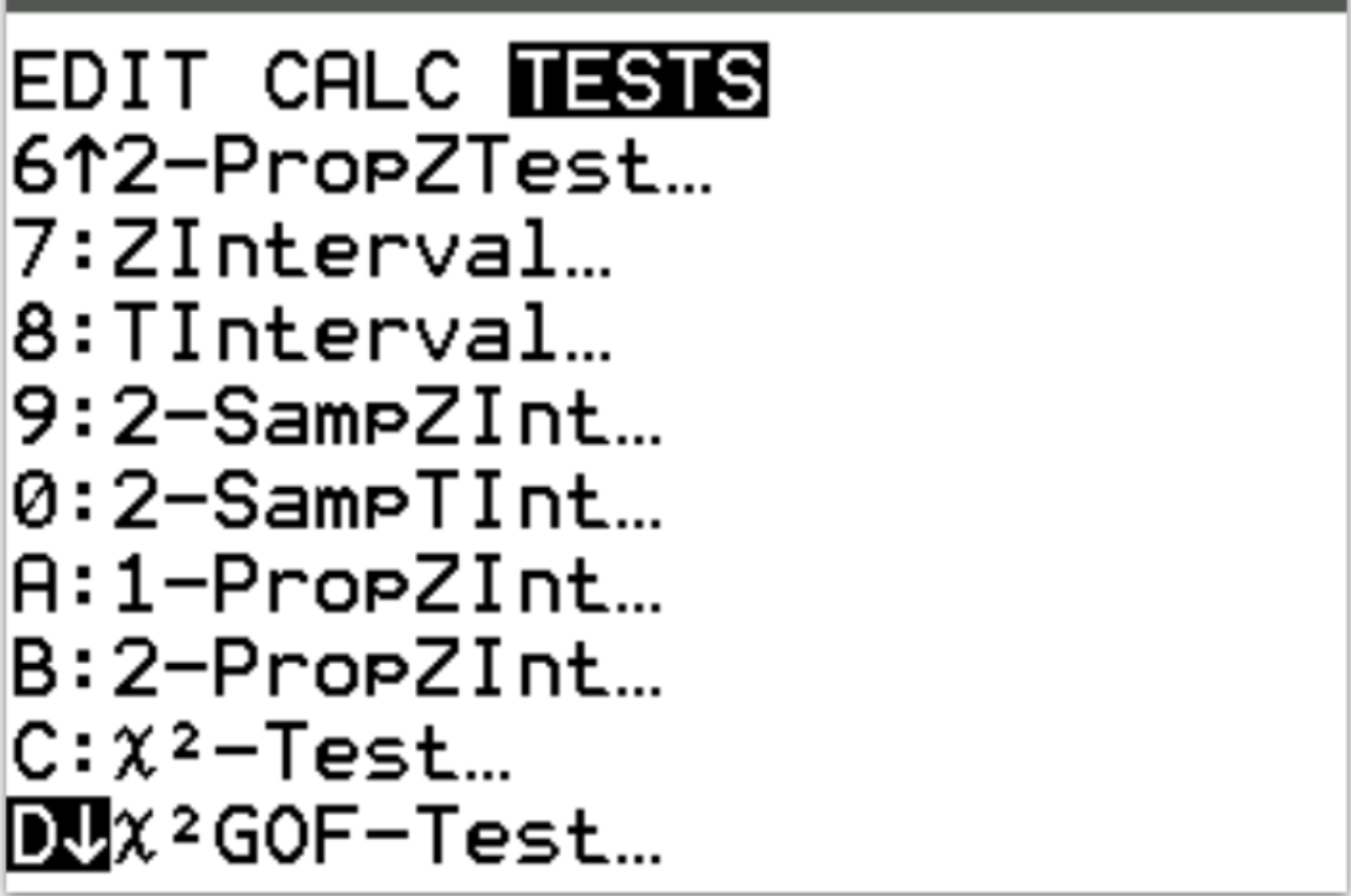
Para Observado , escolha a lista L1. Para Expected , escolha a lista L2. Para df (graus de liberdade), insira #categories – 1. No nosso caso, temos 5-1 = 4. Em seguida, destaque Calcular e pressione Enter .

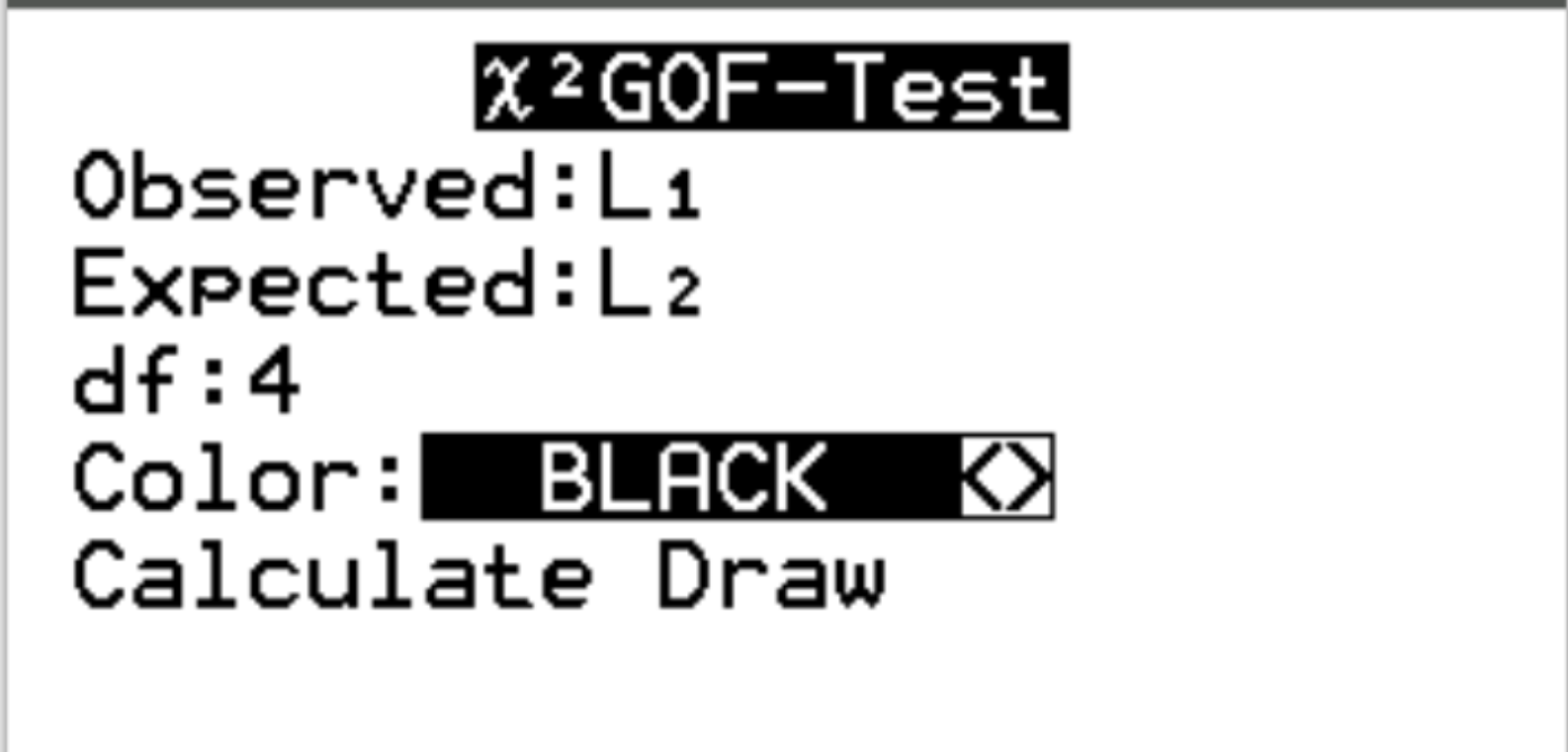
A seguinte saída aparecerá automaticamente:

Etapa 3: interprete os resultados.

A estatística de teste ^X2 para o teste é 4,36 e o valor p correspondente é 0,3595 . Como esse valor p não é inferior a 0,05, não rejeitamos a hipótese nula. Isso significa que não temos evidências suficientes para afirmar que a verdadeira distribuição dos clientes é diferente daquela relatada pelo lojista.