Como usar cdf normal em r (com exemplos)

Você pode usar os seguintes métodos para trabalhar com o CDF normal (função de distribuição cumulativa) em R:

Método 1: calcular probabilidades normais de CDF

 #calculate probability that random value is less than 1.96 in normal CDF
pnorm(1.96)

#calculate probability that random value is greater than 1.96 in normal CDF
pnorm(1.96, lower.tail = FALSE )

Método 2: traçar o CDF normal

 #define sequence of x-values
x <- seq(-4, 4, .01)

#calculate normal CDF probabilities
prob <- pnorm(x)
 
#normal plot CDF
plot(x, prob, type=" l ")

Os exemplos a seguir mostram como usar esses métodos na prática.

Exemplo 1: Calcular probabilidades normais de CDF

O código a seguir mostra como calcular a probabilidade de uma variável aleatória assumir um valor menor que 1,96 em uma distribuição normal padrão:

 #calculate probability that random value is less than 1.96 in normal CDF
pnorm(1.96)

[1] 0.9750021

A probabilidade de uma variável aleatória assumir um valor inferior a 1,96 em uma distribuição normal padrão é 0,975 .

Também podemos encontrar a probabilidade de uma variável aleatória assumir um valor maior que 1,96 usando o argumento lower.tail :

 #calculate probability that random value is greater than 1.96 in normal CDF
pnorm(1.96, lower.tail = FALSE )

[1] 0.0249979

E podemos usar a seguinte sintaxe para encontrar a probabilidade de uma variável aleatória assumir um valor entre dois valores em uma distribuição normal padrão:

 #calculate probability that random value takes on value between -1.96 and 1.96
pnorm(1.96) - pnorm(-1.96)

[1] 0.9500042

A probabilidade de uma variável aleatória assumir um valor entre -1,96 e 1,96 em uma distribuição normal padrão é 0,95 .

Exemplo 2: Traçando o CDF Normal

O código a seguir mostra como plotar um CDF normal:

 #define sequence of x-values
x <- seq(-4, 4, .01)

#calculate normal CDF probabilities
prob <- pnorm(x)
 
#normal plot CDF
plot(x, prob, type=" l ") 

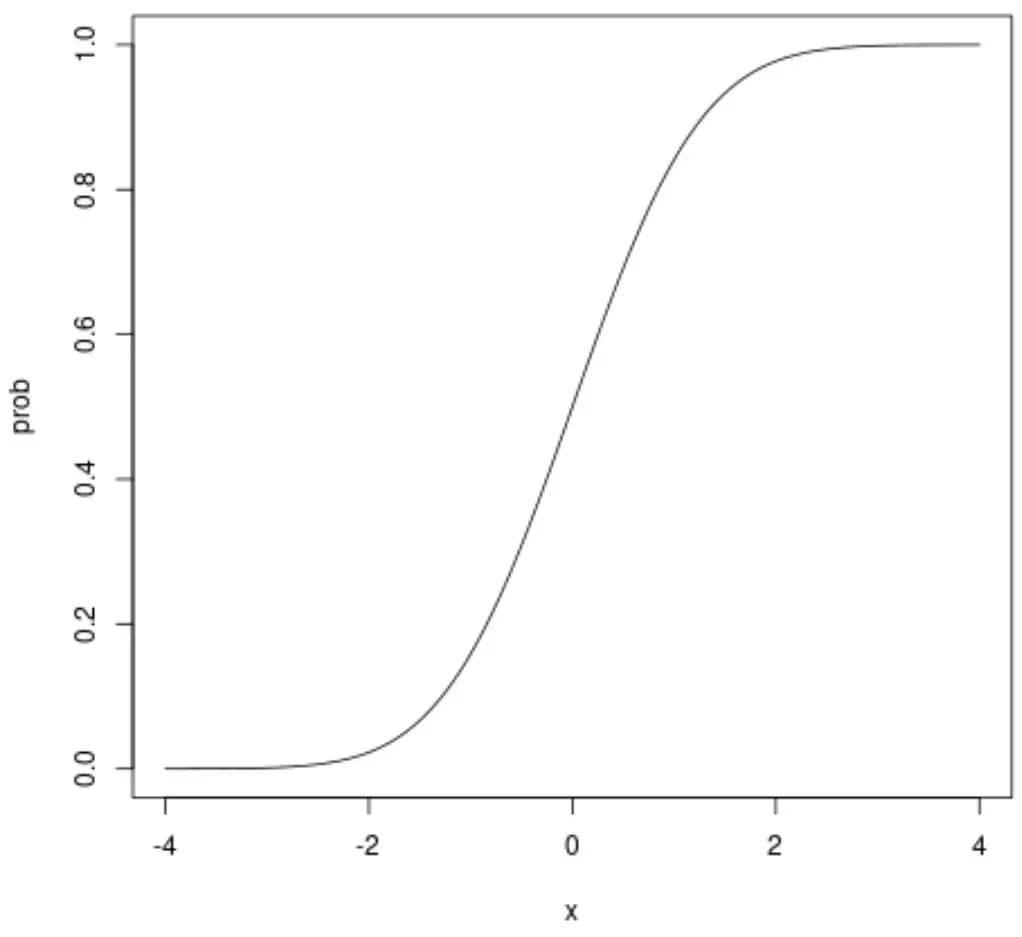
O eixo x mostra os valores de uma variável aleatória que segue uma distribuição normal padrão e o eixo y mostra a probabilidade de uma variável aleatória assumir um valor menor que o valor mostrado no eixo x.

Por exemplo, se olharmos para x = 1,96, veremos que a probabilidade cumulativa de x ser menor que 1,96 é de aproximadamente 0,975:

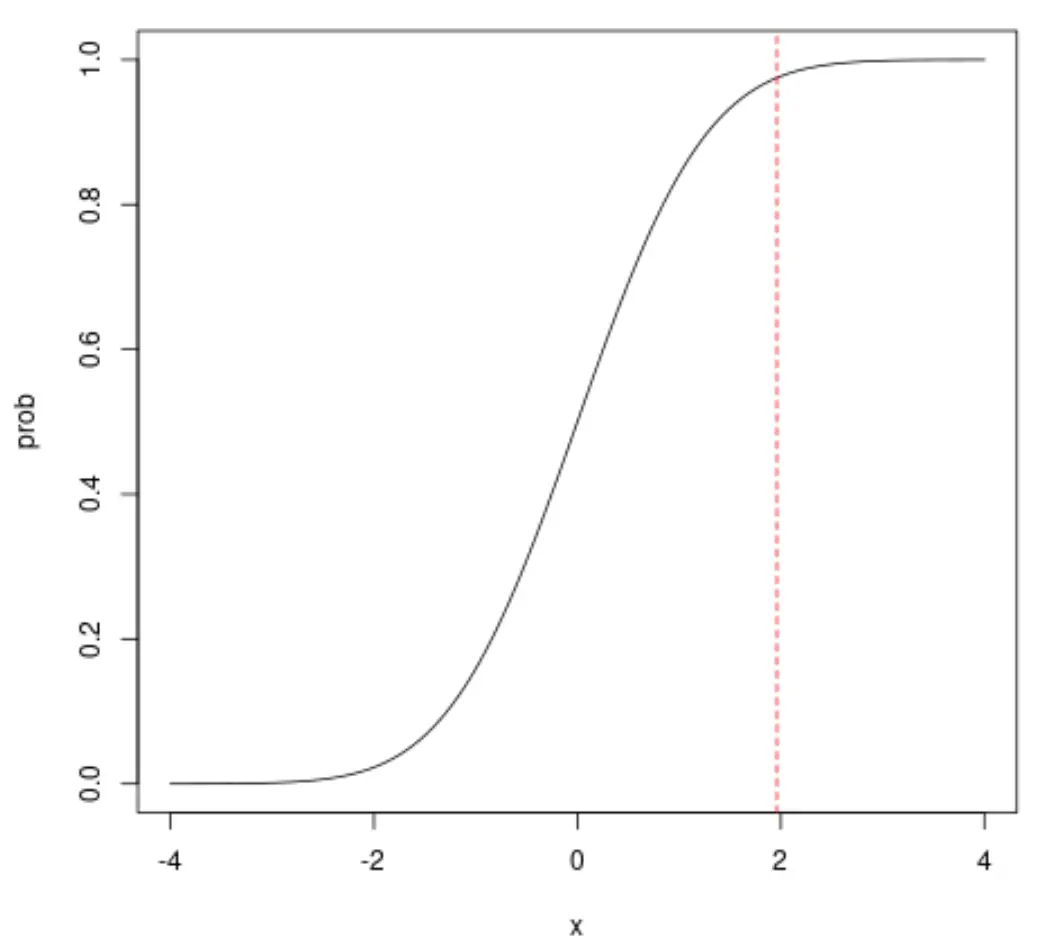
Observe que você também pode alterar a estética do gráfico CDF normal:

 #define sequence of x-values
x <- seq(-4, 4, .01)

#calculate normal CDF probabilities
prob <- pnorm(x)
 
#normal plot CDF
plot(x, prob, type=' l ', col=' blue ', lwd= 2 , main=' Normal CDF ', ylab=' Cumulative Prob ') 

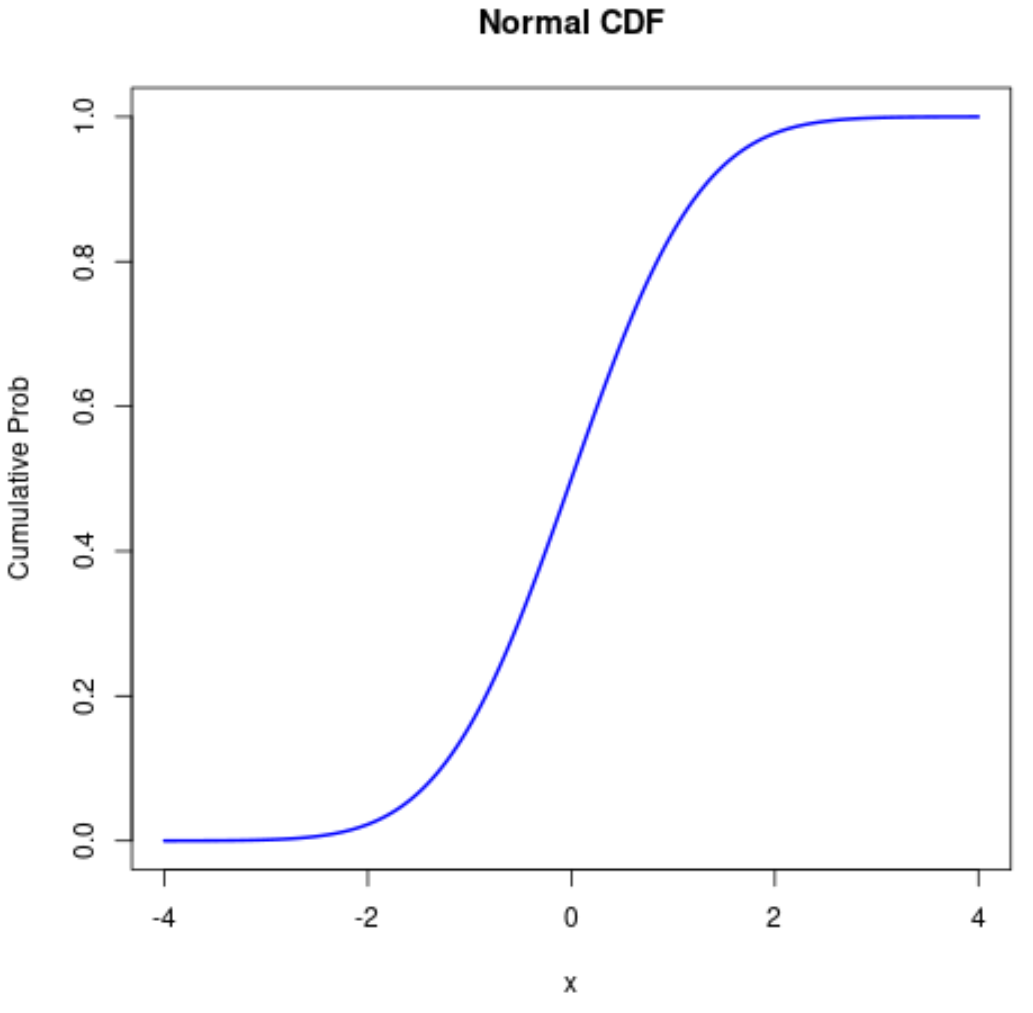
Relacionado: Como usar a função seq em R

Recursos adicionais

Os tutoriais a seguir explicam como realizar outras operações comuns em R:

Como traçar uma distribuição normal em R
Como calcular pontuações Z em R
Um guia para dnorm, pnorm, qnorm e rnorm em R