Cercas superiores e inferiores: definição e exemplo

Nas estatísticas, os limites superior e inferior representam valores limite para valores discrepantes superiores e inferiores em um conjunto de dados. Eles são calculados da seguinte forma:

• Fechamento inferior = Q1 – (1,5*IQR)
• Fechamento superior = Q3 + (1,5*IQR)

onde IQR significa “intervalo interquartil”, que representa a diferença entre o percentil 75 (Q3) e o percentil 25 (Q1) em um conjunto de dados.

Uma observação localizada acima da barreira superior ou abaixo da barreira inferior é frequentemente considerada um valor atípico.

Exemplo: Cálculo da cerca superior e inferior

Suponha que temos o seguinte conjunto de dados:

 Dataset: 11, 13, 14, 14, 15, 16, 18, 22, 24, 27, 34, 36, 38, 41, 45

Podemos usar as seguintes etapas para calcular a cerca superior e inferior do conjunto de dados:

Etapa 1: pesquise Q1 e Q3.

Q1 representa o 25º percentil do conjunto de dados e Q3 representa o 75º percentil. De acordo com a calculadora do intervalo interquartil, Q1 e Q3 para este conjunto de dados são:

• T1: 14
• T3: 36

Etapa 2: Encontre o IQR (intervalo interquartil).

O intervalo interquartil representa a diferença entre Q3 e Q1, que é calculado da seguinte forma:

• Escala interquartil: Q3 – Q1 = 36 – 14 = 22

Etapa 3: Encontre a cerca superior e inferior

Podemos usar as seguintes fórmulas para calcular as cercas superior e inferior:

• Fechamento inferior: Q1 – (1,5*IQR) = 14 – (1,5*22) = -19
• Cerca superior: Q3 + (1,5*IQR) = 36 + (1,5*22) = 69

Como nenhuma das observações em nosso conjunto de dados fica abaixo da cerca inferior ou acima da cerca superior, nenhuma das observações seria considerada atípica.

Também podemos criar um boxplot para visualizar nossa distribuição de valores de dados, bem como as cercas superior e inferior:

Bônus: Calculadora de fechamento superior e inferior

Em vez de calcular manualmente as bordas superior e inferior de um conjunto de dados, sinta-se à vontade para usar a calculadora das bordas superior e inferior:

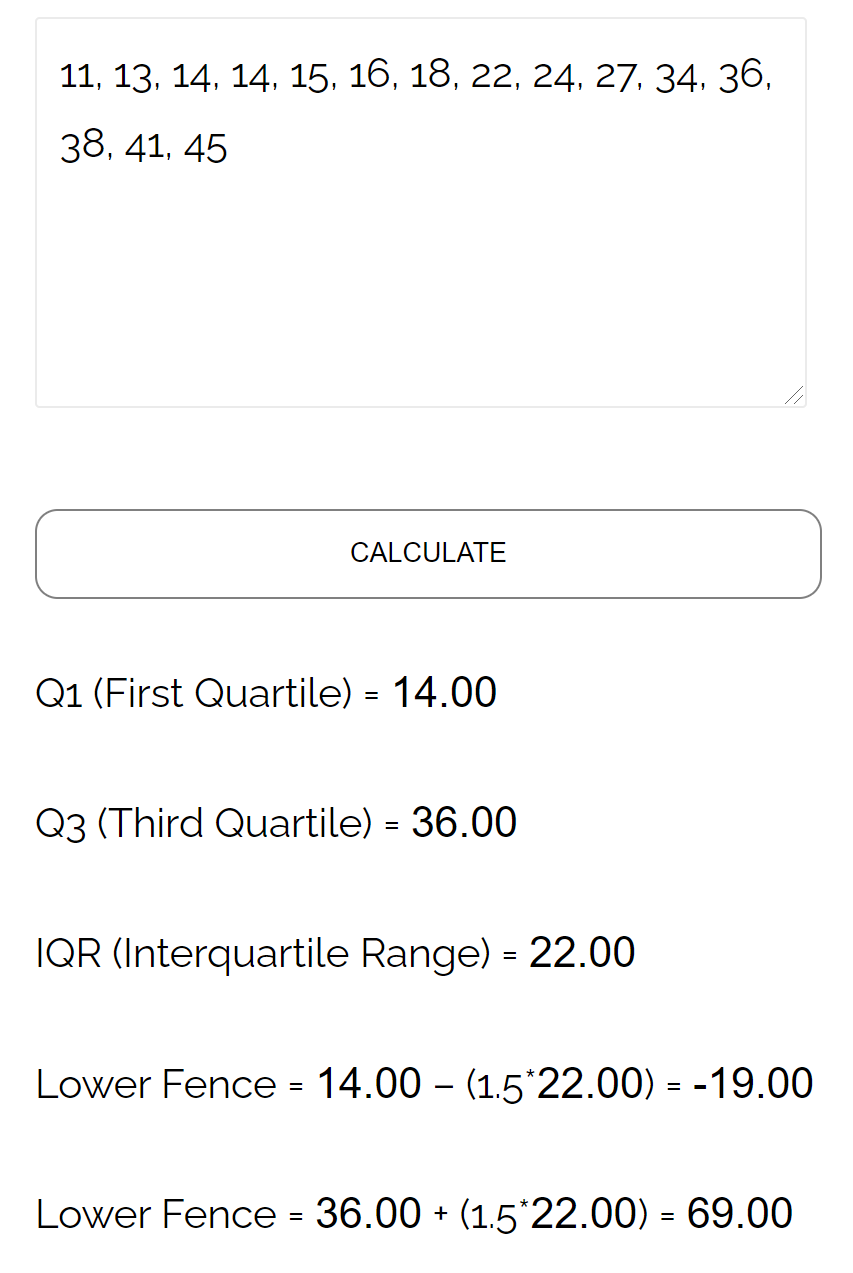
Você pode encontrar calculadoras estatísticas mais úteis nesta página .