Coeficiente de correlação intraclasse: definição + exemplo

Um coeficiente de correlação intraclasse (ICC) é usado para medir a confiabilidade das pontuações em estudos onde há dois ou mais avaliadores.

O valor de um ICC pode variar de 0 a 1, sendo 0 indicando nenhuma confiabilidade entre os avaliadores e 1 indicando confiabilidade perfeita entre os avaliadores.

Simplificando, um ICC é usado para determinar se os itens (ou tópicos) podem ser avaliados de forma confiável por diferentes avaliadores.

Existem várias versões diferentes de um ICC que podem ser calculadas, dependendo dos três fatores a seguir:

• Modelo: efeitos aleatórios unidirecionais, efeitos aleatórios bidirecionais ou efeitos mistos bidirecionais
• Tipo de relacionamento: consistência ou acordo absoluto
• Unidade: avaliador único ou média de avaliadores

Aqui está uma breve descrição dos três modelos diferentes:

1. Modelo de efeitos aleatórios unidirecionais: Este modelo assume que cada sujeito é avaliado por um grupo diferente de avaliadores selecionados aleatoriamente. Com este modelo, os avaliadores são considerados a fonte dos efeitos aleatórios. Este modelo raramente é utilizado na prática porque geralmente é utilizado o mesmo grupo de avaliadores para avaliar cada assunto.

2. Modelo de efeitos aleatórios bidirecionais: Este modelo assume que um grupo de avaliadores k é selecionado aleatoriamente de uma população e então usado para avaliar os sujeitos. Usando este modelo, avaliadores e sujeitos são considerados fontes de efeitos aleatórios. Este modelo é frequentemente utilizado quando queremos generalizar nossos resultados para avaliadores semelhantes aos utilizados no estudo.

3. Modelo de efeitos mistos bidirecional: Este modelo também assume que um grupo de avaliadores k é selecionado aleatoriamente de uma população e então usado para avaliar os sujeitos. No entanto, este modelo assume que o grupo de avaliadores que escolhemos são os únicos avaliadores de interesse, o que significa que não queremos generalizar os nossos resultados para outros avaliadores que também possam partilhar características semelhantes aos avaliadores utilizados no estudo.

Aqui está uma breve descrição dos dois tipos diferentes de relacionamentos que podemos querer medir:

1. Consistência: Estamos interessados nas diferenças sistemáticas entre as classificações dos juízes (por exemplo, os juízes classificaram tópicos semelhantes como baixos e altos?)

2. Concordância absoluta: estamos interessados nas diferenças absolutas entre as pontuações dos juízes (por exemplo, qual é a diferença absoluta entre as pontuações do juiz A e do juiz B?)

Aqui está uma breve descrição das duas unidades diferentes que podem nos interessar:

1. Revisor único: Queremos usar apenas as classificações de um único revisor como base para medição.

2. Média do avaliador: Queremos usar a média das pontuações de todos os juízes como base para medição.

Nota: Se quiser medir o nível de concordância entre dois avaliadores que falham cada um dos itens num resultado dicotómico , deverá utilizar o Kappa de Cohen .

Como interpretar o coeficiente de correlação intraclasse

Veja como interpretar o valor de um coeficiente de correlação intraclasse, segundo Koo & Li :

• Menos de 0,50: baixa confiabilidade
• Entre 0,5 e 0,75: Confiabilidade moderada
• Entre 0,75 e 0,9: Boa confiabilidade
• Maior que 0,9: Excelente confiabilidade

O exemplo a seguir mostra como calcular um coeficiente de correlação intraclasse na prática.

Exemplo: Cálculo do coeficiente de correlação intraclasse

Suponha que quatro juízes diferentes sejam solicitados a avaliar a qualidade de 10 vestibulares diferentes. Os resultados são mostrados abaixo:

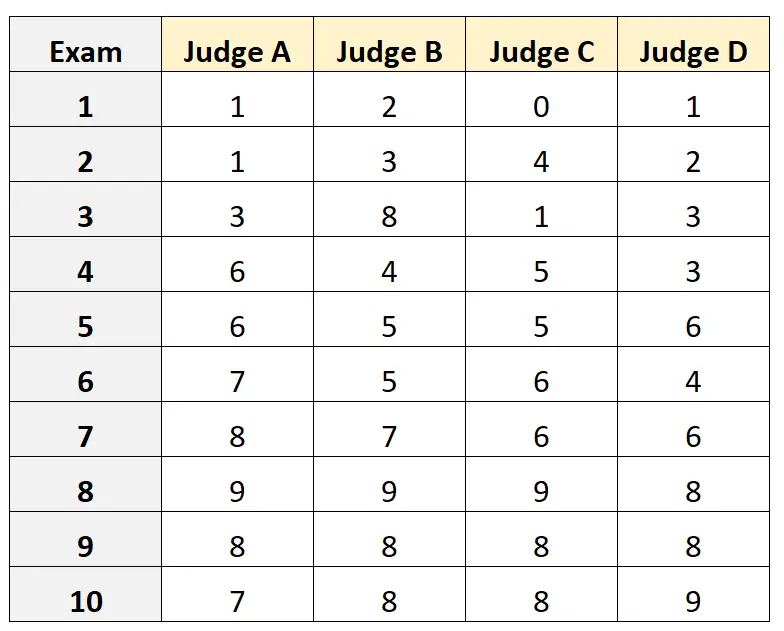
Suponha que os quatro juízes foram selecionados aleatoriamente de uma população de juízes qualificados para o vestibular e queríamos medir a concordância absoluta entre os juízes e queríamos usar as pontuações da perspectiva de apenas um avaliador como base de nossa medição.

Podemos usar o seguinte código em R para ajustar um modelo de efeitos aleatórios bidirecional , usando concordância absoluta como a relação entre avaliadores e usando a unidade única como unidade de interesse:

 #load the interrater reliability package
library (irr)

#define data
data <- data. frame (A=c(1, 1, 3, 6, 6, 7, 8, 9, 8, 7),
                   B=c(2, 3, 8, 4, 5, 5, 7, 9, 8, 8),
                   C=c(0, 4, 1, 5, 5, 6, 6, 9, 8, 8),
                   D=c(1, 2, 3, 3, 6, 4, 6, 8, 8, 9))

#calculate ICC
icc(data, model = " twoway ", type = " agreement ", unit = " single ")

   Model: twoway 
   Type: agreement 

   Subjects = 10 
     Failures = 4 
   ICC(A,1) = 0.782

 F-Test, H0: r0 = 0; H1: r0 > 0 
    F(9.30) = 15.3, p = 5.93e-09 

 95%-Confidence Interval for ICC Population Values:
  0.554 < ICC < 0.931

O coeficiente de correlação intraclasse (CCI) foi de 0,782 .

Com base nas regras práticas para interpretação do ICC, concluiríamos que um ICC de 0,782 indica que os exames podem ser pontuados com “boa” confiabilidade por diferentes avaliadores.

Recursos adicionais

Os tutoriais a seguir fornecem explicações detalhadas sobre como calcular o ICC em diferentes softwares estatísticos:

Como calcular o coeficiente de correlação intraclasse no Excel
Como calcular o coeficiente de correlação intraclasse em R
Como calcular o coeficiente de correlação intraclasse em Python