Coeficiente de determinação (r ao quadrado)

Este artigo explica o que é o coeficiente de determinação (ou R quadrado) nas estatísticas. Assim, você descobrirá como calcular o coeficiente de determinação, como ele é interpretado e, além disso, uma calculadora online para calcular o coeficiente de determinação de uma amostra de dados.

Qual é o coeficiente de determinação (R ao quadrado)?

O coeficiente de determinação , cujo símbolo é R ² ( R ao quadrado ), é uma estatística que mede a qualidade do ajuste de um modelo de regressão. O coeficiente de determinação mostra o quão bem um modelo de regressão se ajusta a um conjunto de dados, ou seja, indica o percentual explicado pelo modelo de regressão.

Portanto, quanto maior o coeficiente de determinação, melhor será o modelo de regressão. Embora esta condição nem sempre seja satisfeita, estamos, em princípio, interessados num coeficiente de determinação tão grande quanto possível. Veremos a seguir como interpretar o coeficiente de determinação.

Fórmula de determinação do coeficiente

O coeficiente de determinação é igual a um menos a razão entre a variância residual e a variância da variável dependente. O coeficiente de determinação também pode ser calculado subtraindo um menos a soma dos quadrados dos resíduos sobre a soma total dos quadrados.

Assim, a fórmula de cálculo do coeficiente de determinação é a seguinte:

Ouro:

• 

  é o coeficiente de determinação.

• 

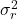
  é a variância residual.

• 

  é a variância da variável dependente Y.

• 

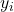
  é o valor da variável dependente da observação i.

• 

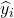
  é o valor aproximado pelo modelo de regressão para observação i.

• 

  é a média da variável dependente em todas as observações.

👉 Você pode usar a calculadora abaixo para calcular o coeficiente de determinação para qualquer conjunto de dados.

Para o caso do modelo de regressão linear, o coeficiente de determinação equivale ao quadrado do coeficiente de correlação :

Ouro

é a covariância das variáveis X e Y,

E

são as variâncias da variável independente X e da variável dependente Y, respectivamente.

Calculadora de coeficiente de determinação

Insira dados de amostra na calculadora abaixo para ajustar um modelo de regressão linear simples e calcular seu coeficiente de determinação. É necessário separar os pares de dados, para que na primeira caixa existam apenas os valores da variável independente X e na segunda caixa existam apenas os valores da variável dependente Y.

Os dados devem ser separados por espaço e inseridos usando o ponto final como separador decimal.

Interpretação do coeficiente de determinação

Nesta seção veremos como interpretar o coeficiente de determinação, pois não adianta saber o valor do coeficiente de determinação se você não souber o que significa posteriormente.

O valor do coeficiente de determinação pode variar de 0 a 1, porém, normalmente é expresso em porcentagem, portanto o mínimo é 0% e o máximo é 100%.

Quanto à interpretação do coeficiente de determinação , quanto maior o seu valor significa que o modelo de regressão explica melhor a amostra de dados. Assim, quanto mais próximo o coeficiente de determinação estiver de 1, mais ajustado será o modelo. Por outro lado, quanto mais próximo de 0, menos confiável será o modelo de regressão produzido.

Porém, ao comparar dois modelos de regressão, o modelo com maior coeficiente de regressão nem sempre é melhor. Por exemplo, um modelo de regressão pode ter um coeficiente de regressão R ² = 100% porque muitas variáveis explicativas foram adicionadas ao modelo e, portanto, pode explicar perfeitamente todas as observações. Mas este modelo certamente faz uma previsão muito pobre para um novo valor que não foi usado para construir o modelo de regressão.

Deve-se também ter em mente que o modelo de regressão resultante atende aos pressupostos anteriores. Assim, um modelo com coeficiente de determinação muito alto é inútil se a variabilidade de seus resíduos não for constante (homocedasticidade).

Além disso, o coeficiente de determinação apresenta um limite importante, pois não penaliza a inclusão de variáveis explicativas. Logicamente, quanto mais variáveis explicativas um modelo de regressão tiver, mais complexo será o modelo, mas melhor explicará os dados observados e, portanto, maior será o coeficiente de determinação. Porém, o coeficiente de determinação ajustado leva em consideração a quantidade de variáveis do modelo (veremos como ele é calculado a seguir).

Concluindo, o coeficiente de determinação é muito útil para analisar um modelo de regressão porque nos permite saber até que ponto o modelo de regressão se ajusta ao conjunto de dados. Contudo, outras ferramentas também devem ser utilizadas para revisar o modelo resultante, como gráficos estatísticos .

Coeficiente de determinação ajustado

O coeficiente de determinação ajustado , também chamado de coeficiente de determinação ajustado , mede a qualidade do ajuste de um modelo de regressão levando em consideração o número de variáveis explicativas incluídas no modelo.

A diferença entre o coeficiente de determinação e o coeficiente de determinação ajustado é que o coeficiente de determinação mede a qualidade do ajuste sem levar em conta o número de variáveis, por outro lado, o coeficiente de determinação ajustado mede a qualidade do ajuste penalizando para cada variável adicionada.

A fórmula de cálculo do coeficiente de determinação ajustado é a seguinte:

Ouro:

• 

  é o coeficiente de determinação ajustado.

• 

  é o coeficiente de determinação.

• 

  é o tamanho da amostra.

• 

  é o número de variáveis explicativas no modelo de regressão.

Portanto, o coeficiente de determinação ajustado é melhor que o coeficiente de determinação para comparação de dois modelos diferentes, uma vez que os modelos podem ter um número diferente de variáveis explicativas.