Como calcular um coeficiente phi em r

Um coeficiente Phi (às vezes chamado de coeficiente de contingência quadrático médio ) é uma medida da associação entre duas variáveis binárias.

Para uma tabela 2×2 dada para duas variáveis aleatórias x e y :

O coeficiente Phi pode ser calculado da seguinte forma:

Φ = (AD-BC) / √ (A+B)(C+D)(A+C)(B+D)

Exemplo: Cálculo de um coeficiente Phi em R

Suponhamos que queremos saber se o género está ou não associado à preferência por um partido político. Então pegamos numa amostra aleatória simples de 25 eleitores e perguntamos-lhes sobre a sua preferência por um partido político.

A tabela a seguir apresenta os resultados da pesquisa:

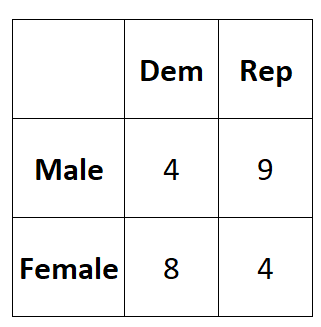
Podemos usar o seguinte código para inserir esses dados em uma matriz 2×2 em R:

 #create 2x2 table
data = matrix(c(4, 8, 9, 4), nrow = 2 )

#view dataset
data

     [,1] [,2]
[1,] 4 9
[2,] 8 4

Podemos então usar a função phi() do pacote psych para calcular o coeficiente Phi entre as duas variáveis:

 #load psych package
library (psych)

#calculate Phi Coefficient
phi(data)

[1] -0.36

O coeficiente Phi é -0,36 .

Observe que a função phi arredonda para 2 dígitos por padrão, mas você pode especificar a função para arredondar para quantos dígitos desejar:

 #calculate Phi Coefficient and round to 6 digits
phi(data, digits = 6 )

[1] -0.358974

Como interpretar um coeficiente Phi

Semelhante a um coeficiente de correlação de Pearson, um coeficiente Phi assume valores entre -1 e 1 onde:

• -1 indica uma relação perfeitamente negativa entre as duas variáveis.
• 0 indica nenhuma associação entre as duas variáveis.
• 1 indica uma relação perfeitamente positiva entre as duas variáveis.

Em geral, quanto mais longe um coeficiente Phi estiver de zero, mais forte será a relação entre as duas variáveis.

Em outras palavras, quanto mais longe um coeficiente Phi estiver de zero, mais evidências haverá de algum tipo de padrão sistemático entre as duas variáveis.

Recursos adicionais

Uma introdução ao coeficiente Phi
Calculadora de coeficiente Phi