Como interpretar o erro padrão residual

O erro padrão residual é usado para medir quão bem um modelo de regressão se ajusta a um conjunto de dados.

Em termos simples, mede o desvio padrão dos resíduos num modelo de regressão.

É calculado da seguinte forma:

Erro padrão residual = √ Σ(y – ŷ) ² /df

Ouro:

• y: O valor observado
• ŷ: O valor previsto
• df: Os graus de liberdade, calculados como o número total de observações – número total de parâmetros do modelo.

Quanto menor o erro padrão residual, melhor o modelo de regressão se ajusta a um conjunto de dados. Por outro lado, quanto maior o erro padrão residual, pior o modelo de regressão se ajusta a um conjunto de dados.

Um modelo de regressão que possui um pequeno erro padrão residual terá pontos de dados fortemente agrupados em torno da linha de regressão ajustada:

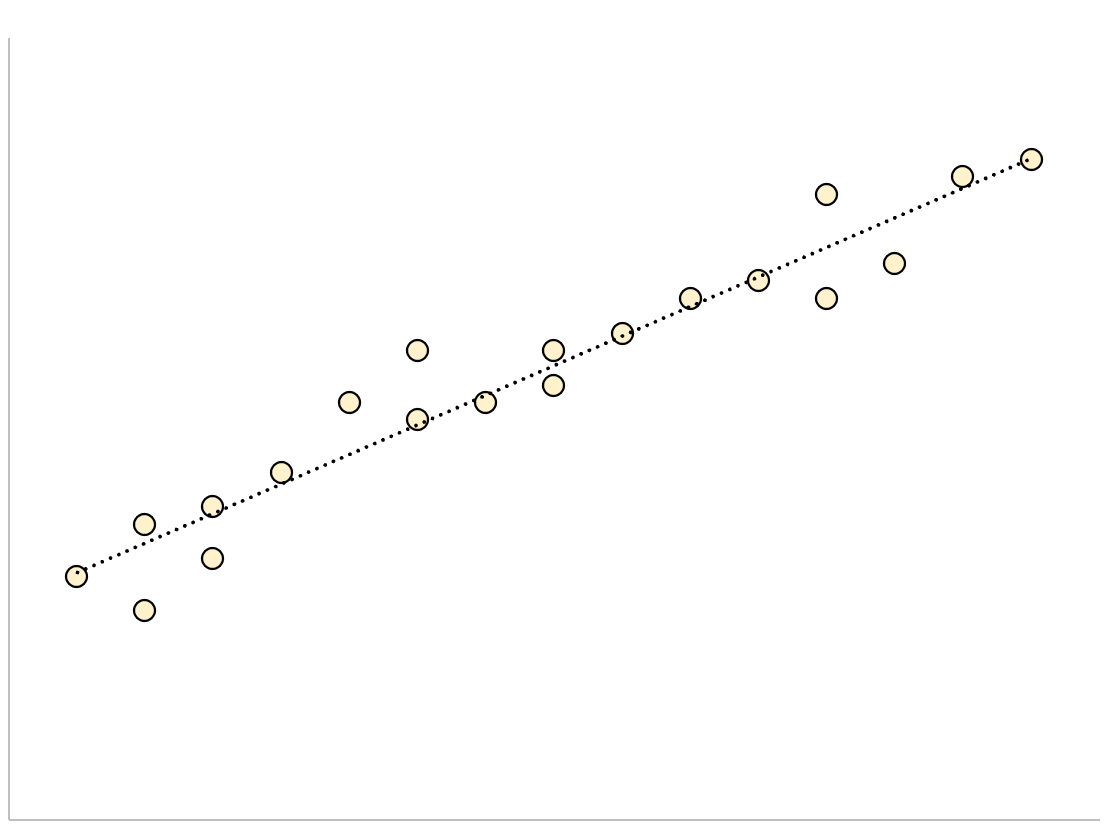
Os resíduos deste modelo (a diferença entre os valores observados e os valores previstos) serão pequenos, o que significa que o erro padrão residual também será pequeno.

Por outro lado, um modelo de regressão que tenha um grande erro padrão residual terá pontos de dados mais vagamente espalhados em torno da linha de regressão ajustada:

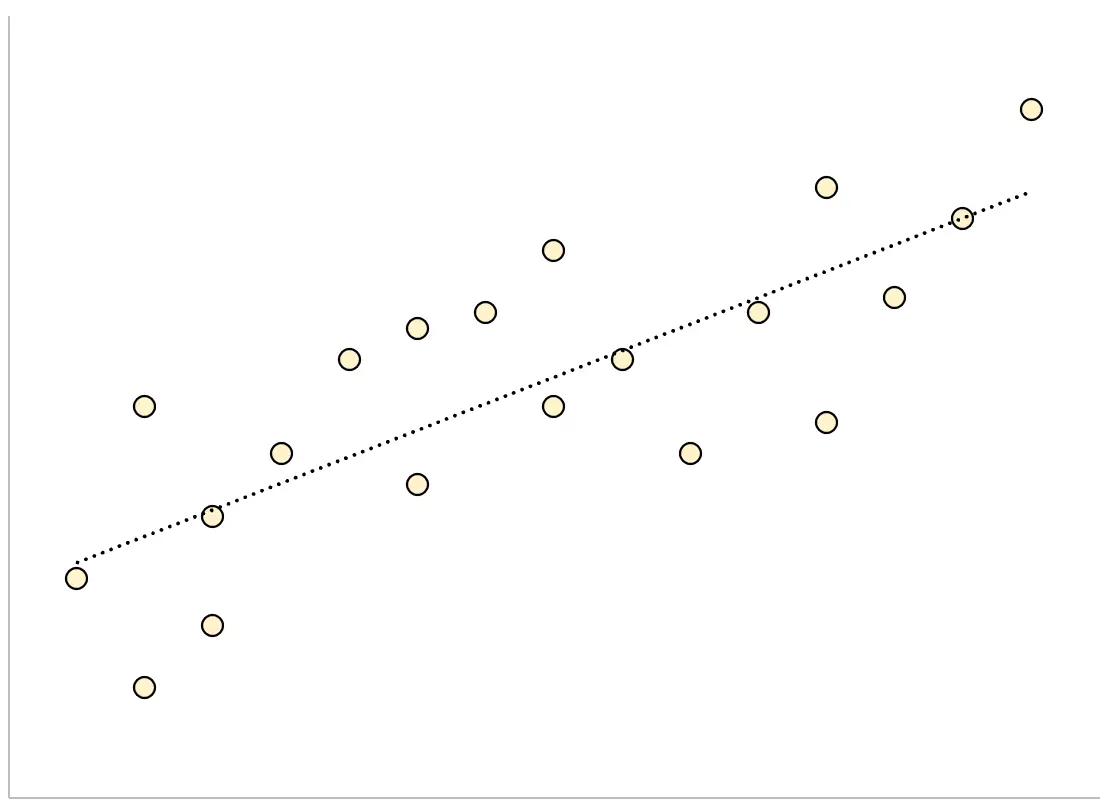
Os resíduos deste modelo serão maiores, o que significa que o erro padrão residual também será maior.

O exemplo a seguir mostra como calcular e interpretar o erro padrão residual de um modelo de regressão em R.

Exemplo: Interpretando o erro padrão residual

Suponha que queiramos ajustar o seguinte modelo de regressão linear múltipla:

mpg = β ₀ + β ₁ (deslocamento) + β ₂ (potência)

Este modelo usa as variáveis preditoras “deslocamento” e “cavalo-vapor” para prever as milhas por galão percorridas por um determinado carro.

O código a seguir mostra como ajustar esse modelo de regressão em R:

 #load built-in mtcars dataset
data(mtcars)

#fit regression model
model <- lm(mpg~disp+hp, data=mtcars)

#view model summary
summary(model)

Call:
lm(formula = mpg ~ disp + hp, data = mtcars)

Residuals:
    Min 1Q Median 3Q Max 
-4.7945 -2.3036 -0.8246 1.8582 6.9363 

Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept) 30.735904 1.331566 23.083 < 2nd-16 ***
available -0.030346 0.007405 -4.098 0.000306 ***
hp -0.024840 0.013385 -1.856 0.073679 .  
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 3.127 on 29 degrees of freedom
Multiple R-squared: 0.7482, Adjusted R-squared: 0.7309 
F-statistic: 43.09 on 2 and 29 DF, p-value: 2.062e-09

Na parte inferior do resultado, podemos ver que o erro padrão residual deste modelo é 3,127 .

Isso nos diz que o modelo de regressão prevê o consumo de combustível do carro com um erro médio de cerca de 3.127.

Usando erro padrão residual para comparar modelos

O erro padrão residual é particularmente útil para comparar o ajuste de diferentes modelos de regressão.

Por exemplo, suponha que ajustemos dois modelos de regressão diferentes para prever o consumo de automóveis. O erro padrão residual de cada modelo é o seguinte:

• Erro padrão residual do modelo 1: 3,127
• Erro padrão residual do modelo 2: 5,657

Como o Modelo 1 tem um erro padrão residual menor, ele se ajusta melhor aos dados do que o Modelo 2. Assim, preferiríamos usar o Modelo 1 para prever o mpg do carro, porque as previsões que ele faz estão mais próximas dos valores de mpg observados dos carros.

Recursos adicionais

Como realizar regressão linear simples em R
Como realizar regressão linear múltipla em R
Como criar um gráfico residual em R