Como ler uma matriz de covariância

A covariância é uma medida de como as mudanças em uma variável estão associadas às mudanças em uma segunda variável. Mais especificamente, é uma medida do grau em que duas variáveis estão linearmente associadas.

Uma matriz de covariância é uma matriz quadrada que mostra a covariância entre muitas variáveis diferentes. Esta pode ser uma forma útil de compreender como diferentes variáveis estão relacionadas em um conjunto de dados.

O exemplo a seguir mostra como ler uma matriz de covariância na prática.

Como ler uma matriz de covariância

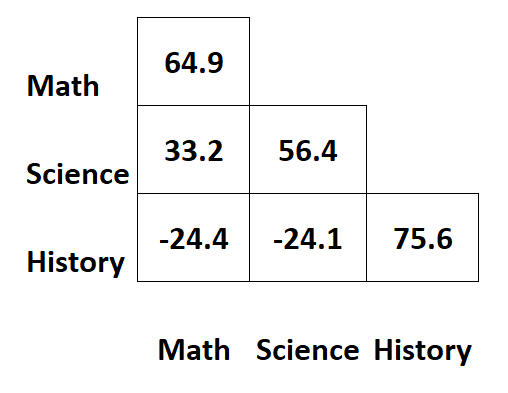
Suponha que temos a seguinte matriz de covariância que contém informações sobre as notas dos exames de três disciplinas diferentes para os alunos:

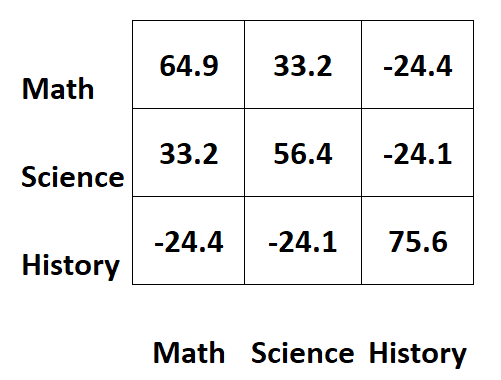
Os valores ao longo das diagonais da matriz representam as variâncias de cada sujeito.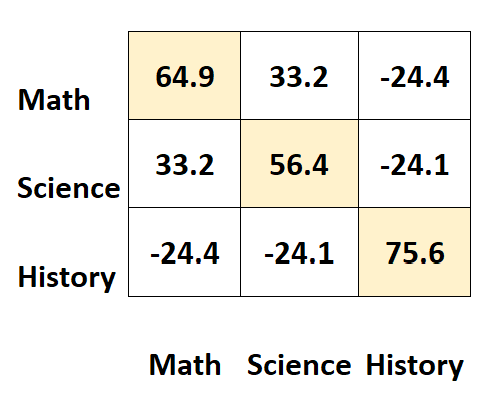

Por exemplo:

• A variância dos resultados matemáticos é 64,9 .
• A variância das pontuações em ciências é 56,4 .
• A variância das pontuações históricas é 75,6 .

Os demais valores da matriz representam as covariâncias entre os diferentes assuntos.

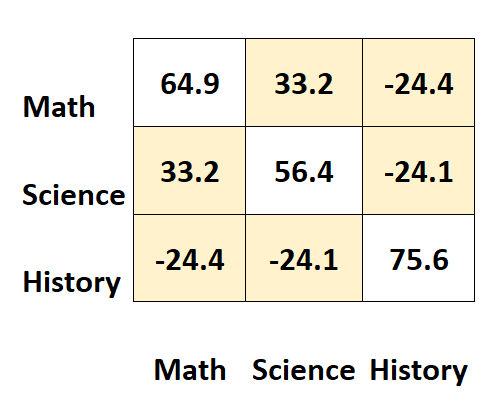
Por exemplo:

• A covariância entre as pontuações em matemática e ciências é 33,2 .
• A covariância entre as pontuações em matemática e história é –24,4 .
• A covariância entre as pontuações de ciência e história é –24,1 .

Um número positivo para covariância indica que duas variáveis tendem a aumentar ou diminuir em conjunto.

Por exemplo, matemática e ciências têm uma covariância positiva ( 33,2 ), indicando que os alunos com notas altas em matemática também tendem a ter notas altas em ciências.

Por outro lado, os alunos com mau desempenho em matemática também tendem a ter mau desempenho em ciências.

Um número negativo para covariância indica que à medida que uma variável aumenta, uma segunda variável tende a diminuir.

Por exemplo, matemática e história têm uma covariância negativa ( -24,44 ), indicando que os alunos com alto desempenho em matemática tendem a ter baixo desempenho em história.

Por outro lado, os alunos com notas baixas em matemática tendem a ter notas altas em história.

Uma nota sobre a simetria de uma matriz de covariância

Deve-se notar que uma matriz de covariância é perfeitamente simétrica.

Por exemplo, a célula superior direita mostra exatamente o mesmo valor que a célula inferior esquerda:

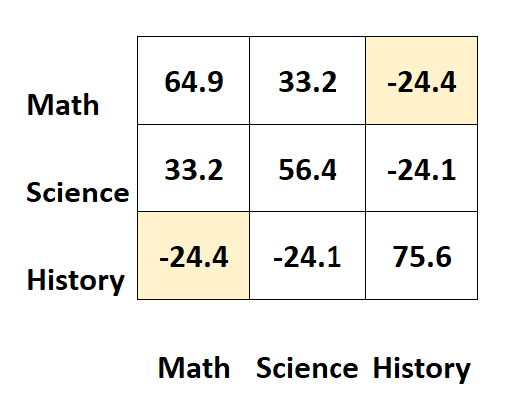
Na verdade, as duas células medem a covariância entre história e matemática.

Como uma matriz de covariância é simétrica, metade dos valores de covariância exibidos na matriz são redundantes e desnecessários.

Então, às vezes, apenas metade da matriz de covariância será exibida:

Quando usar uma matriz de covariância

Na prática, muitas vezes você precisará criar e interpretar uma matriz de correlação com mais frequência do que uma matriz de covariância.

No entanto, matrizes de covariância são frequentemente usadas “nos bastidores” para diferentes algoritmos e modelos de aprendizado de máquina.

Por exemplo, a matriz de covariância é usada durante a análise de componentes principais , o que nos ajuda a compreender os padrões subjacentes em um conjunto de dados contendo um grande número de variáveis.

Recursos adicionais

Os tutoriais a seguir explicam como criar uma matriz de covariância usando diferentes softwares estatísticos:

Como criar uma matriz de covariância em R
Como criar uma matriz de covariância em Python
Como criar uma matriz de covariância no SPSS
Como criar uma matriz de covariância no Excel