Como ler um box plot com outliers (com exemplo)

Um box plot é um tipo de gráfico que exibe o resumo de cinco dígitos de um conjunto de dados, que inclui:

• O valor mínimo
• O primeiro quartil (o 25º percentil)
• O valor mediano
• O terceiro quartil (o 75º percentil)
• O valor máximo

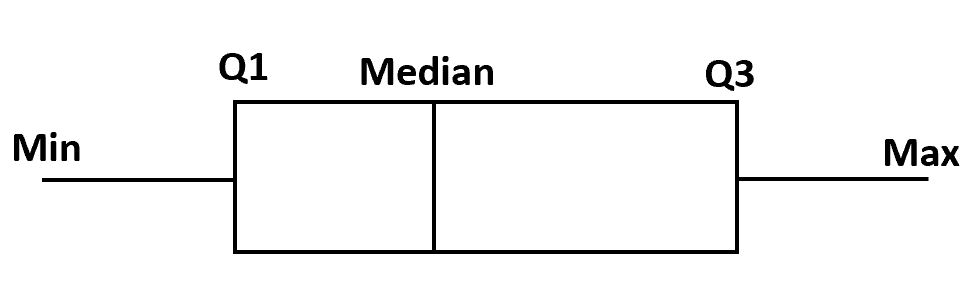
Para fazer um box plot, primeiro desenhamos uma caixa do primeiro ao terceiro quartil.

A seguir, traçamos uma linha vertical na mediana.

Por fim, traçamos “bigodes” dos quartis até o valor mínimo e máximo.

Na maioria dos softwares estatísticos, uma observação é definida como discrepante se atender a um dos dois requisitos a seguir:

• A observação é 1,5 vezes o intervalo interquartil abaixo do primeiro quartil (Q1)
• A observação é 1,5 vezes o intervalo interquartil acima do terceiro quartil (Q3).

Se existir um valor discrepante em um conjunto de dados, ele geralmente será rotulado com um pequeno ponto fora da faixa de bigodes no gráfico de caixa:

Quando isso acontece, aos valores “mínimo” e “máximo” no boxplot são simplesmente atribuídos os valores de Q1 – 1,5*IQR e Q3 + 1,5*IQR, respectivamente.

O exemplo a seguir mostra como interpretar gráficos de caixa com e sem valores discrepantes.

Exemplo: Interpretando um Box Plot com Outliers

Suponha que criemos os dois box plots a seguir para visualizar a distribuição de pontos marcados por jogadores de basquete de dois times diferentes:

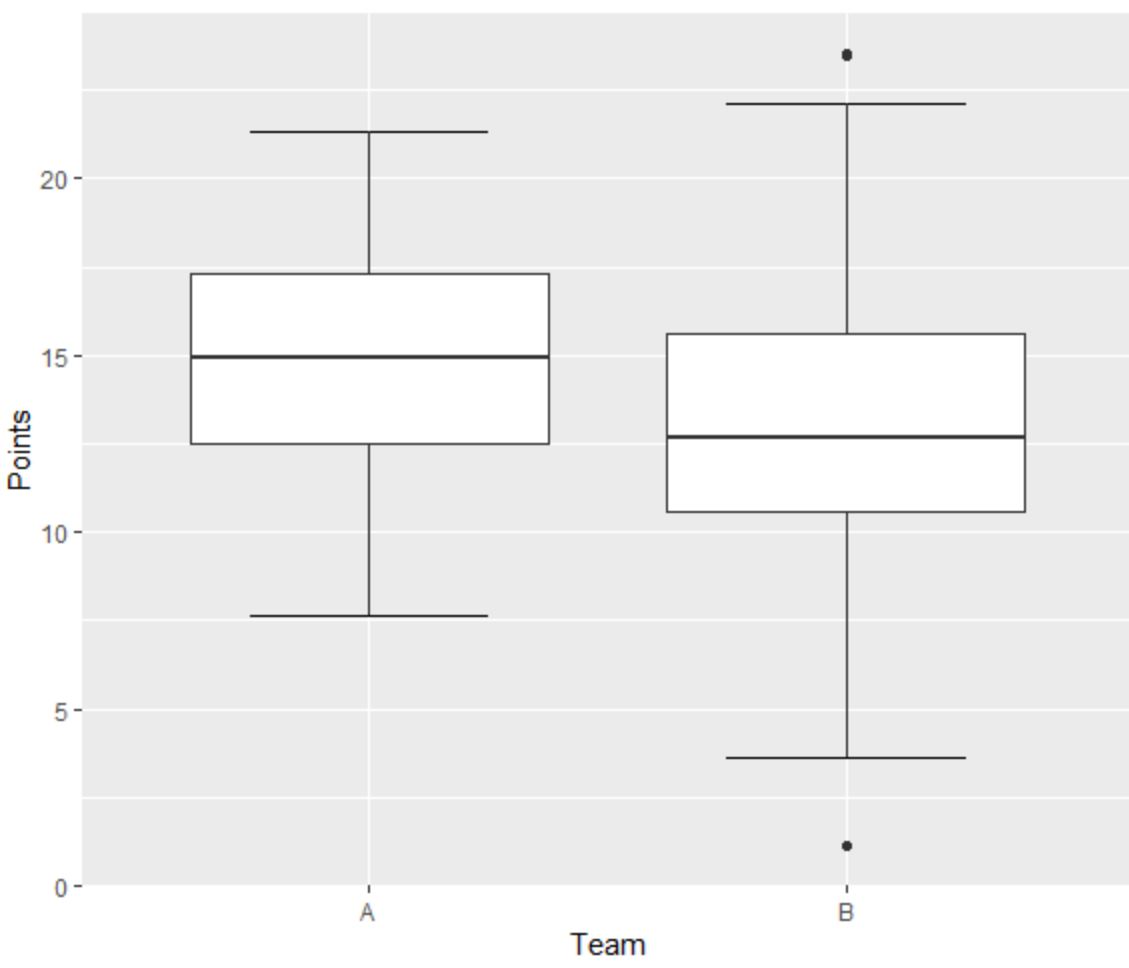
O boxplot esquerdo para o Time A não tem valores discrepantes, pois não há pequenos pontos localizados fora do bigode mínimo ou máximo.

No entanto, o boxplot certo para a Equipe B tem um valor discrepante acima do valor “máximo” e um valor discrepante abaixo do valor “mínimo”.

Aqui está o resumo atual de cinco dígitos para a distribuição da variável “Pontos” para a Equipe B:

• Valor mínimo: 1,1
• Primeiro quartil: 10,5
• Mediana: 12,7
• Terceiro quartil: 15,6
• Valor máximo: 23,5

Veja como calcular os limites de possíveis valores discrepantes:

Escala interquartil : Terceiro quartil – Primeiro quartil = 15,6 – 10,5 = 5,1

Limite inferior : Q1 – 1,5*IQR = 10,5 – 1,5*5,1 = 2,85

Limite superior : Q3 + 1,5*IQR = 15,6 + 1,5*5,1 = 23,25

Os bigodes para os valores mínimo e máximo no boxplot são colocados em 2,85 e 23,25 .

Assim, observações com valores de 1,1 e 23,5 se qualificam como valores discrepantes no boxplot porque estão fora dos limites inferior e superior.

Bônus : aqui está o código exato que usamos para criar esses dois boxplots na linguagem de programação R:

 library (ggplot2)

#make this example reproducible 
set. seeds (2)

#create data frame
df <- data. frame (Team = factor(rep(c("A", "B"), each = 200)), 
                 Points = c(rnorm(200, mean = 15, sd = 3), 
                           rnorm(200, mean = 12, sd = 4))) 

#create box plots
ggplot(df, aes(x = Team, y = Points)) +
  stat_boxplot(geom = " errorbar ", width = 0.5) +  
  geom_boxplot() 

#calculate summary statistics for each team
tapply(df$Points, df$Team, summary)

Recursos adicionais

Os tutoriais a seguir fornecem informações adicionais sobre box plots:

Como comparar gráficos de caixa
Como identificar assimetria em box plots
Como encontrar o intervalo interquartil de um boxplot