Como ler uma matriz de correlação

Nas estatísticas, muitas vezes procuramos compreender a relação entre duas variáveis.

Por exemplo, podemos querer compreender a relação entre o número de horas que um aluno estuda e a nota que recebe no exame.

Uma forma de quantificar esta relação é utilizar o coeficiente de correlação de Pearson , que é uma medida da associação linear entre duas variáveis . Tem um valor entre -1 e 1 onde:

• -1 indica uma correlação linear perfeitamente negativa entre duas variáveis
• 0 indica nenhuma correlação linear entre duas variáveis
• 1 indica uma correlação linear perfeitamente positiva entre duas variáveis

Quanto mais longe o coeficiente de correlação estiver de zero, mais forte será a relação entre as duas variáveis.

Relacionado: O que é considerado uma correlação “forte”?

Mas, em alguns casos, queremos compreender a correlação entre múltiplos pares de variáveis. Nestes casos, podemos criar uma matriz de correlação , que é uma tabela quadrada que mostra os coeficientes de correlação entre diversas variáveis.

Exemplo de matriz de correlação

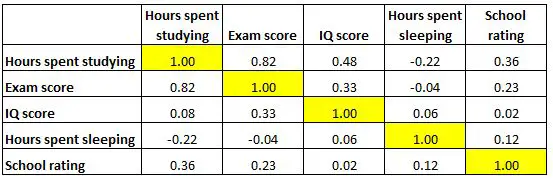
A matriz de correlação abaixo apresenta os coeficientes de correlação entre diversas variáveis relacionadas à educação:

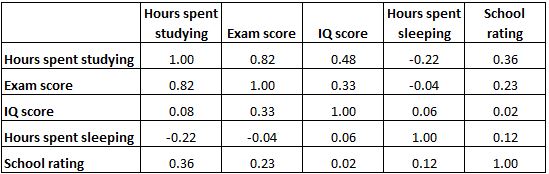
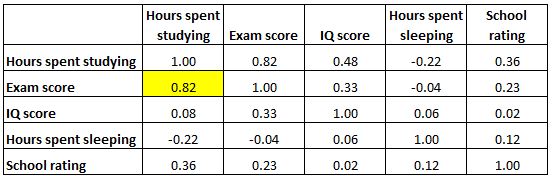
Cada célula da tabela mostra a correlação entre duas variáveis específicas. Por exemplo, a célula destacada abaixo mostra que a correlação entre “horas gastas estudando” e “nota no exame” é de 0,82 , indicando que elas estão fortemente correlacionadas positivamente. Mais horas gastas estudando estão intimamente ligadas a pontuações mais altas nos exames.

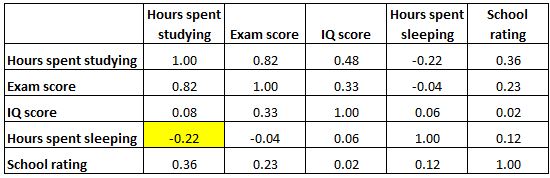
E a célula destacada abaixo mostra que a correlação entre “horas gastas estudando” e “horas gastas dormindo” é -0,22 , indicando que elas estão fracamente correlacionadas negativamente. Mais horas gastas estudando estão associadas a menos horas gastas dormindo.

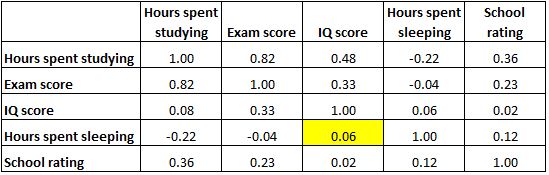
E a célula destacada abaixo mostra que a correlação entre “horas passadas dormindo” e “pontuação de QI” é de 0,06 , indicando que elas são basicamente não correlacionadas. Há muito pouca associação entre o número de horas que um aluno dorme e a sua pontuação de QI.

Observe também que os coeficientes de correlação ao longo da diagonal da tabela são todos iguais a 1 porque cada variável está perfeitamente correlacionada consigo mesma. Essas células não são úteis para interpretação.

Variações da matriz de correlação

Observe que uma matriz de correlação é perfeitamente simétrica. Por exemplo, a célula superior direita mostra exatamente o mesmo valor que a célula inferior esquerda:

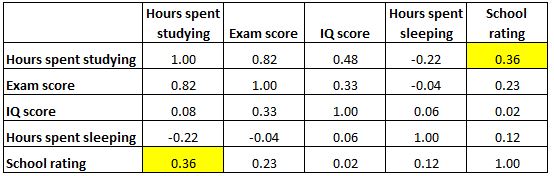
Na verdade, as duas células medem a correlação entre “horas de estudo” e “nota escolar”.

Como uma matriz de correlação é simétrica, metade dos coeficientes de correlação exibidos na matriz são redundantes e desnecessários. Então, às vezes, apenas metade da matriz de correlação será exibida:

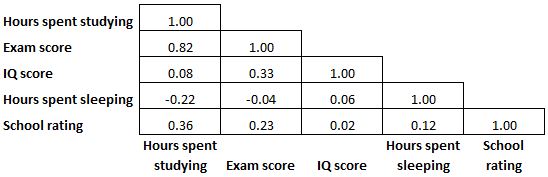
E às vezes uma matriz de correlação será colorida como um mapa de calor para tornar os coeficientes de correlação ainda mais fáceis de ler:

Quando usar uma matriz de correlação

Na prática, uma matriz de correlação é comumente usada por três motivos:

1. Uma matriz de correlação resume convenientemente um conjunto de dados.

Uma matriz de correlação é uma maneira simples de resumir as correlações entre todas as variáveis em um conjunto de dados. Por exemplo, suponha que temos o seguinte conjunto de dados contendo as seguintes informações para 1.000 alunos:

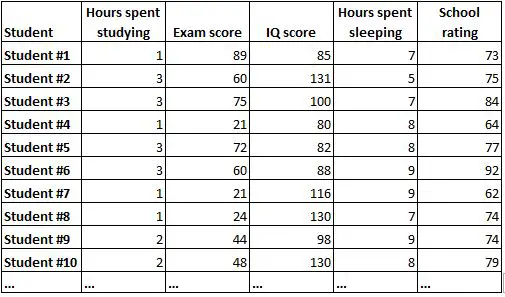
Seria muito difícil compreender a relação entre cada variável apenas olhando os dados brutos. Felizmente, uma matriz de correlação pode nos ajudar a compreender rapidamente as correlações entre cada par de variáveis.

2. Uma matriz de correlação serve como diagnóstico para a regressão.

Uma das principais suposições da regressão linear múltipla é que nenhuma variável independente no modelo está fortemente correlacionada com qualquer outra variável no modelo.

Quando duas variáveis independentes são altamente correlacionadas, isso resulta em um problema denominado multicolinearidade e pode dificultar a interpretação dos resultados da regressão.

Uma das maneiras mais simples de detectar um possível problema de multicolinearidade é observar uma matriz de correlação e verificar visualmente se alguma das variáveis está altamente correlacionada entre si.

3. Uma matriz de correlação pode ser usada como entrada para outras análises.

Uma matriz de correlação é usada como entrada para outras análises complexas, como análise fatorial exploratória e modelos de equações estruturais.

Recursos adicionais

Os tutoriais a seguir explicam como criar uma matriz de correlação usando vários softwares estatísticos:

Como criar uma matriz de correlação no Excel
Como criar uma matriz de correlação no SPSS
Como criar uma matriz de correlação no Stata
Como criar uma matriz de correlação em Python