Como usar a tabela z (com exemplos)

Uma tabela z é uma tabela que informa qual porcentagem de valores fica abaixo de uma determinada pontuação z em uma distribuição normal padrão.

Uma pontuação z simplesmente informa quantos desvios padrão um valor de dados individual cai da média. É calculado da seguinte forma:

pontuação z = (x – μ) / σ

Ouro:

• x: valor de dados individuais
• μ: média populacional
• σ: desvio padrão populacional

Este tutorial mostra vários exemplos de uso da tabela z.

Exemplo 1

As notas em um determinado vestibular têm distribuição normal com média μ = 82 e desvio padrão σ = 8. Aproximadamente qual porcentagem de alunos tem pontuação abaixo de 84 no exame?

Etapa 1: Encontre a pontuação z.

Primeiro, encontraremos a pontuação z associada a uma pontuação de exame de 84:

pontuação z = (x – μ) / σ = (84 – 82) / 8 = 2/8 = 0,25

Passo 2: Use o gráfico z para encontrar a porcentagem que corresponde à pontuação z.

A seguir, procuraremos o valor 0,25 na tabela z:

Cerca de 59,87% dos alunos pontuam abaixo de 84 neste exame.

Exemplo 2

A altura das plantas em um determinado jardim é normalmente distribuída com média de μ = 26,5 polegadas e desvio padrão de σ = 2,5 polegadas. Aproximadamente que porcentagem de plantas tem mais de 26 polegadas de altura?

Etapa 1: Encontre a pontuação z.

Primeiro, encontraremos o escore z associado a uma altura de 26 polegadas.

pontuação z = (x – μ) / σ = (26 – 26,5) / 2,5 = -0,5 / 2,5 = -0,2

Passo 2: Use o gráfico z para encontrar a porcentagem que corresponde à pontuação z.

A seguir procuraremos o valor -0,2   na tabela z:

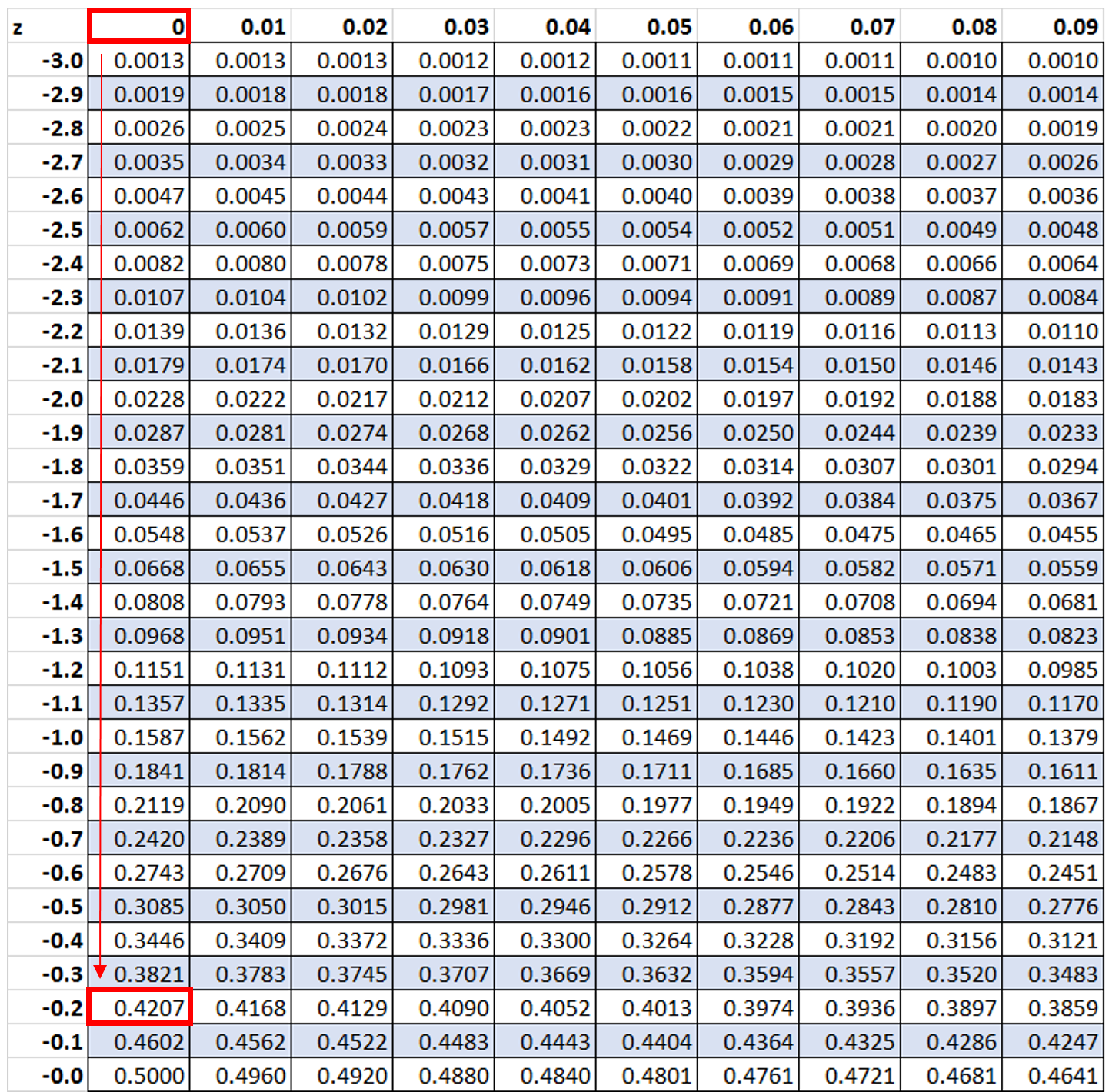
Vemos que 42,07% dos valores estão abaixo de um z-score de -0,2. Porém, neste exemplo queremos saber qual porcentagem de valores é maior que -0,2, o que podemos encontrar usando a fórmula 100% – 42,07% = 57,93%.

Portanto, aproximadamente 59,87% das plantas neste jardim têm mais de 26 centímetros de altura.

Exemplo 3

O peso de uma determinada espécie de golfinho é normalmente distribuído com média μ = 400 libras e desvio padrão de σ = 25 libras. Aproximadamente que porcentagem de golfinhos pesa entre 410 e 425 libras?

Etapa 1: Encontre as pontuações z.

Primeiro, encontraremos as pontuações z associadas a 410 livros e 425 livros

pontuação z de 410 = (x – μ) / σ = (410 – 400) / 25 = 10/25 = 0,4

pontuação z de 425 = (x – μ) / σ = (425 – 400) / 25 = 25/25 = 1

Passo 2: Use o gráfico z para encontrar as porcentagens que correspondem a cada pontuação z.

Primeiro, procuraremos o valor 0,4   na tabela z:

A seguir procuraremos o valor 1   na tabela z:

Por fim, subtrairemos o menor valor do maior valor: 0,8413 – 0,6554 = 0,1859 .

Assim, aproximadamente 18,59% dos golfinhos pesam entre 410 e 425 libras.

Recursos adicionais

Uma introdução à distribuição normal
Calculadora de área de distribuição normal
Calculadora de pontuação Z