Qual é a compensação entre viés e variância no aprendizado de máquina?

Para avaliar o desempenho de um modelo em um conjunto de dados, precisamos medir até que ponto as previsões do modelo correspondem aos dados observados.

Para modelos de regressão , a métrica mais comumente usada é o erro quadrático médio (MSE), que é calculado da seguinte forma:

MSE = (1/n)*Σ(y _i – f(x _i )) ²

Ouro:

• n: número total de observações
• y _i : O valor da resposta da ^i-ésima observação
• f (x _i ): O valor de resposta previsto da i- ^ésima observação

Quanto mais próximas as previsões do modelo estiverem das observações, menor será o MSE.

No entanto, só nos preocupamos com o teste MSE – o MSE quando o nosso modelo é aplicado a dados não vistos. Isso ocorre porque nos preocupamos apenas com o desempenho do modelo em dados desconhecidos, não em dados existentes.

Por exemplo, não há problema se um modelo que prevê preços de ações tiver um MSE baixo em dados históricos, mas realmente queremos poder usar o modelo para prever com precisão dados futuros.

Acontece que o teste MSE ainda pode ser dividido em duas partes:

(1) Variância: refere-se à quantidade que nossa função f mudaria se a estimássemos usando um conjunto de treinamento diferente.

(2) Viés: refere-se ao erro introduzido ao abordar um problema real, que pode ser extremamente complicado, com um modelo muito mais simples.

Escrito em termos matemáticos:

Teste MSE = Var( f̂( x ₀ )) + [Bias( f̂( x ₀ ))] ² + Var(ε)

Teste MSE = Variância + Viés ² + Erro irredutível

O terceiro termo, o erro irredutível, é o erro que não pode ser reduzido por nenhum modelo simplesmente porque sempre há ruído na relação entre o conjunto de variáveis explicativas e a variável resposta .

Modelos que possuem alto viés tendem a ter baixa variância . Por exemplo, os modelos de regressão linear tendem a ter um viés elevado (assumindo uma relação linear simples entre as variáveis explicativas e a variável resposta) e uma variância baixa (as estimativas do modelo não mudarão muito de amostra para amostra). o outro).

No entanto, modelos com baixo viés tendem a ter alta variância . Por exemplo, modelos não lineares complexos tendem a ter baixo viés (não assumem uma certa relação entre as variáveis explicativas e a variável resposta) com alta variância (as estimativas do modelo podem mudar significativamente de uma amostra de aprendizagem para outra).

A compensação entre viés e variância

O trade-off entre viés e variância refere-se ao trade-off que ocorre quando escolhemos reduzir o viés, o que geralmente aumenta a variância, ou reduzir a variância, o que geralmente aumenta o viés.

O gráfico a seguir oferece uma maneira de visualizar essa compensação:

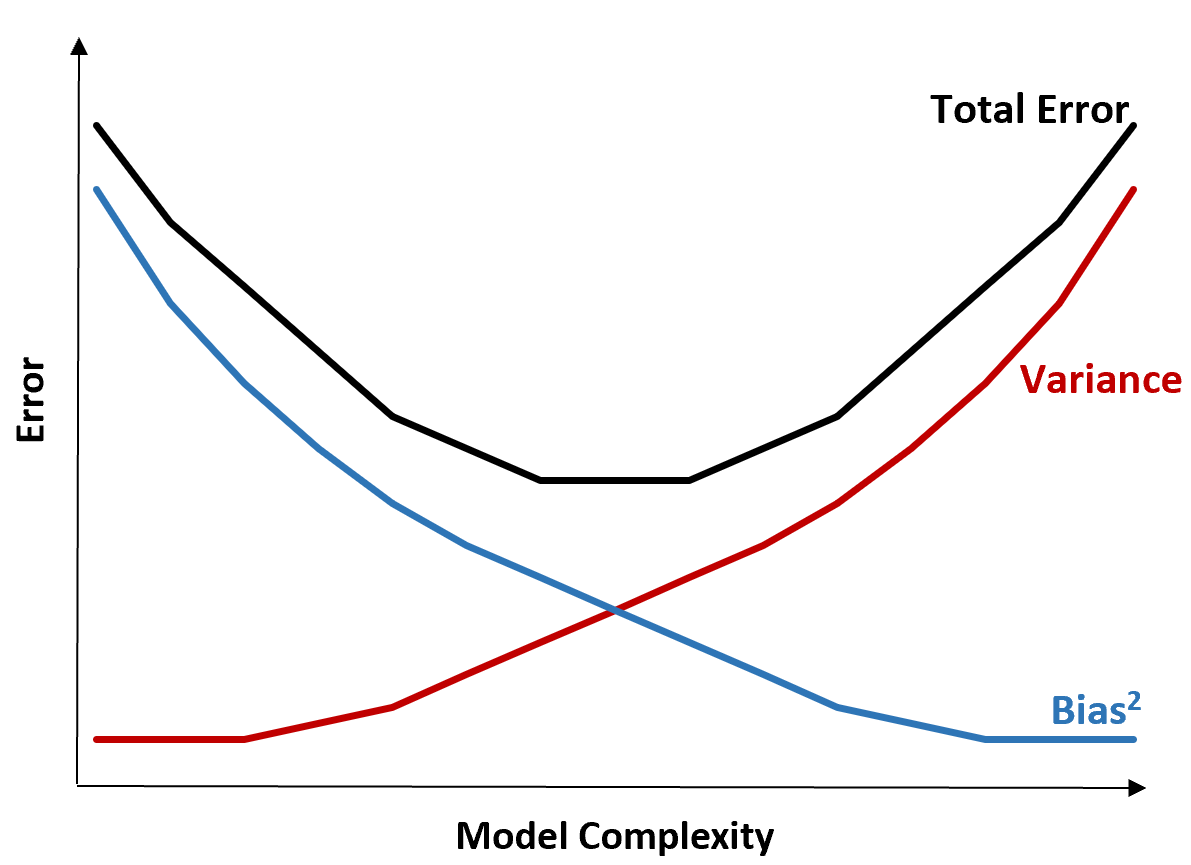
O erro total diminui à medida que a complexidade de um modelo aumenta, mas apenas até certo ponto. Além de um certo ponto, a variância começa a aumentar e o erro total também começa a aumentar.

Na prática, nos preocupamos apenas em minimizar o erro total de um modelo, não necessariamente em minimizar a variância ou viés. Acontece que a maneira de minimizar o erro total é encontrar o equilíbrio certo entre variância e viés.

Em outras palavras, queremos um modelo complexo o suficiente para capturar a verdadeira relação entre as variáveis explicativas e a variável resposta, mas não complexo demais para detectar padrões que na verdade não existem.

Quando um modelo é muito complexo, ele ajusta demais os dados. Isso acontece porque é muito difícil encontrar padrões nos dados de treinamento que sejam simplesmente causados pelo acaso. É provável que esse tipo de modelo tenha um desempenho insatisfatório em dados invisíveis.

Mas quando um modelo é demasiado simples, subestima os dados. Isto acontece porque se assume que a verdadeira relação entre as variáveis explicativas e a variável resposta é mais simples do que realmente é.

A maneira de selecionar modelos ideais em aprendizado de máquina é encontrar um equilíbrio entre viés e variância para minimizar o erro de testar o modelo em dados futuros não vistos.

Na prática, a forma mais comum de minimizar o MSE dos testes é utilizar a validação cruzada .