Como realizar uma correção de bonferroni em r

Uma ANOVA unidirecional é usada para determinar se há ou não uma diferença estatisticamente significativa entre as médias de três ou mais grupos independentes.

Se o valor p geral da tabela ANOVA estiver abaixo de um certo nível de significância, então temos evidências suficientes para dizer que pelo menos uma das médias do grupo é diferente das outras.

No entanto, isso não nos diz quais grupos são diferentes uns dos outros. Isto simplesmente nos diz que nem todas as médias dos grupos são iguais.

Para saber exatamente quais grupos são diferentes entre si, precisamos realizar testes t pareados entre cada grupo enquanto controlamos a taxa de erro familiar .

Uma das maneiras mais comuns de fazer isso é usar a correção de Bonferroni ao calcular valores p para cada um dos testes t pareados.

Este tutorial explica como realizar a correção de Bonferroni em R.

Exemplo: correção de Bonferroni em R

Suponha que um professor queira saber se três técnicas de estudo diferentes levam ou não a resultados diferentes em testes entre os alunos.

Para testar isso, ela designa aleatoriamente 10 alunos para usar cada técnica de estudo. Depois de uma semana usando a técnica de estudo atribuída, cada aluno faz o mesmo exame.

Podemos usar as seguintes etapas em R para ajustar uma ANOVA unidirecional e usar a correção de Bonferroni para calcular as diferenças de pares entre os resultados dos exames de cada grupo.

Etapa 1: crie o conjunto de dados.

O código a seguir mostra como criar um conjunto de dados contendo os resultados dos exames de todos os 30 alunos:

 #create data frame
data <- data.frame(technique = rep (c("tech1", "tech2", "tech3"), each = 10 ),
                   score = c(76, 77, 77, 81, 82, 82, 83, 84, 85, 89,
                             81, 82, 83, 83, 83, 84, 87, 90, 92, 93,
                             77, 78, 79, 88, 89, 90, 91, 95, 95, 98))

#view first six rows of data frame
head(data)

  technical score
1 tech1 76
2 tech1 77
3 tech1 77
4 tech1 81
5 tech1 82
6 tech1 82

Etapa 2: visualize os resultados dos exames de cada grupo.

O código a seguir mostra como produzir boxplots para visualizar a distribuição dos resultados dos exames para cada grupo:

 boxplot(score ~ technique,
        data = data,
        main = "Exam Scores by Studying Technique",
        xlab = "Studying Technique",
        ylab = "Exam Scores",
        col = "steelblue",
        border = "black")

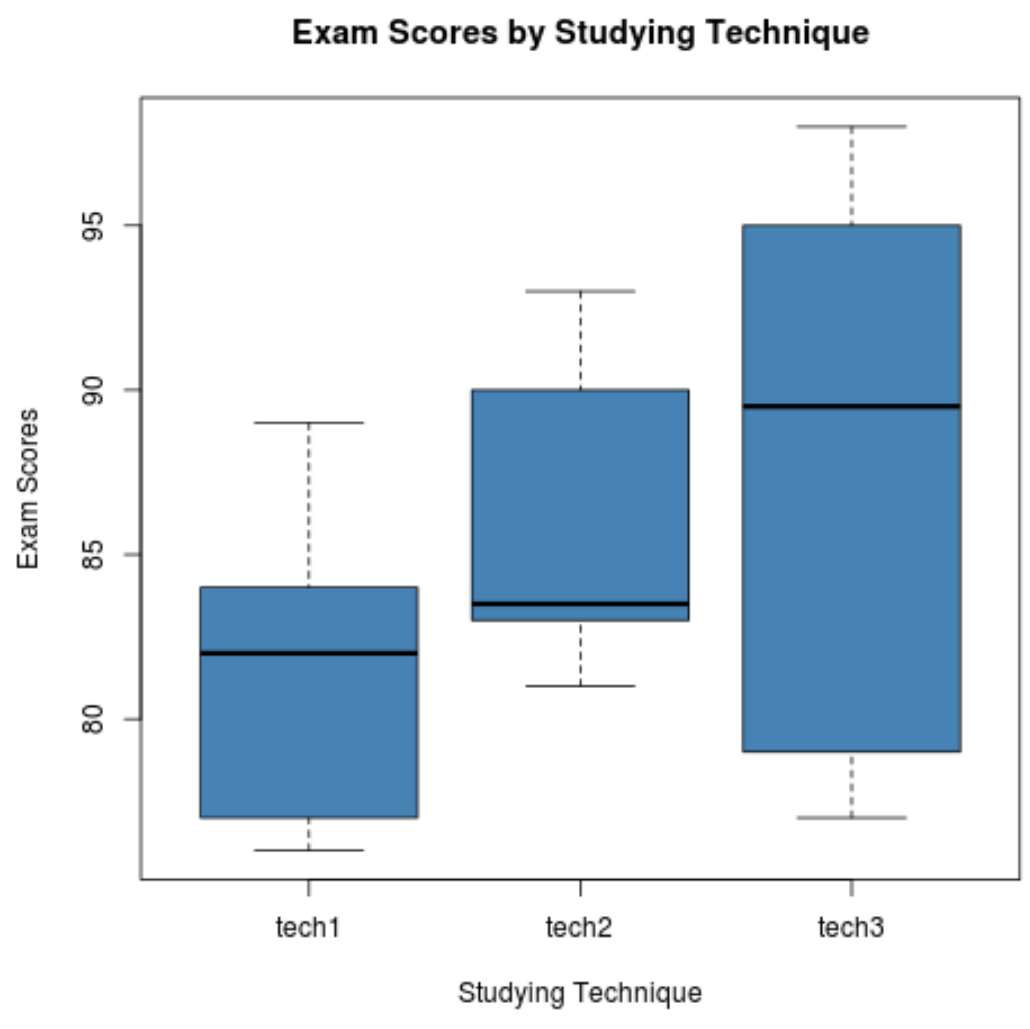
Etapa 3: execute uma ANOVA unidirecional.

O código a seguir mostra como realizar uma ANOVA unidirecional para testar as diferenças entre as pontuações médias dos exames em cada grupo:

 #fit the one-way ANOVA model
model <- aov(score ~ technique, data = data)

#view model output
summary(model)

            Df Sum Sq Mean Sq F value Pr(>F)  
technical 2 211.5 105.73 3.415 0.0476 *
Residuals 27 836.0 30.96                 
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Como o valor p geral ( 0,0476 ) é inferior a 0,05, isso indica que cada grupo não tem a mesma nota média no exame.

A seguir, realizaremos testes t pareados usando a correção de Bonferroni para valores de p para calcular diferenças pareadas entre os resultados dos exames de cada grupo.

Etapa 4: realizar testes t pareados.

Para realizar testes t pareados com correção de Bonferroni em R, podemos usar a função pairwise.t.test() , que usa a seguinte sintaxe:

pairwise.t.test(x, g, p.adjust.method=”bonferroni”)

Ouro:

• x: um vetor numérico de valores de resposta
• g: Um vetor que especifica os nomes dos grupos (por exemplo, técnica de estudo)

O código a seguir mostra como usar esta função em nosso exemplo:

 #perform pairwise t-tests with Bonferroni's correction
pairwise.t.test(data$score, data$technique, p.adjust.method=" bonferroni ")

	Pairwise comparisons using t tests with pooled SD 

data: data$score and data$technique 

      tech1 tech2
tech2 0.309 -    
tech3 0.048 1.000

P value adjustment method: bonferroni

A forma de interpretar o resultado é a seguinte:

• O valor p ajustado para a diferença média nas notas dos exames entre a Técnica 1 e a Técnica 2 é 0,309 .
• O valor p ajustado para a diferença média nas notas dos exames entre a Técnica 1 e a Técnica 3 é 0,048 .
• O valor p ajustado para a diferença média nas notas dos exames entre a Técnica 2 e a Técnica 3 é 1000 .

Com base nos resultados, podemos perceber que a única diferença significativa está entre a técnica 1 e a técnica 3.

Recursos adicionais

Uma introdução à ANOVA unidirecional
Como realizar ANOVA unidirecional em R
Como realizar o teste de Tukey em R
Como realizar o teste de Dunnett em R