Correção de continuidade de yate: definição e exemplo

Um teste de independência do qui-quadrado é usado para determinar se existe ou não uma associação significativa entre duas variáveis categóricas.

Este teste usa as seguintes hipóteses nulas e alternativas:

• H ₀ : (hipótese nula) As duas variáveis são independentes.
• H ₁ : (hipótese alternativa) As duas variáveis não são independentes. (ou seja, eles estão associados)

Usamos a seguinte fórmula para calcular a estatística do teste Qui-quadrado x ² para este teste:

X ² = Σ(O _i -E _i ) ² / E _i

Ouro:

• Σ: é um símbolo sofisticado que significa “soma”
• O: valor observado
• E: valor esperado

Este teste assume que as probabilidades discretas de frequências em uma tabela de contingência podem ser aproximadas pela distribuição Qui-quadrado, que é uma distribuição contínua.

No entanto, esta suposição tende a ser ligeiramente incorreta e as estatísticas de teste resultantes tendem a ser tendenciosas para cima.

Para corrigir esse viés, podemos aplicar a correção de continuidade de Yate , que aplica a seguinte correção à fórmula ^X2 :

X ² = Σ(|O _i -E _i | – 0,5) ² / E _i

Geralmente só usamos essa correção quando pelo menos uma célula da tabela de contingência tem uma frequência esperada menor que 5.

Exemplo: aplicação da correção de continuidade de Yate

Suponhamos que queremos saber se o género está ou não associado à preferência por um partido político. Pegamos uma amostra aleatória simples de 40 eleitores e perguntamos sobre suas preferências partidárias. A tabela a seguir apresenta os resultados da pesquisa:

Veja como realizar um teste de independência qui-quadrado com correção de continuidade de Yate:

Valores observados:

Valores esperados:

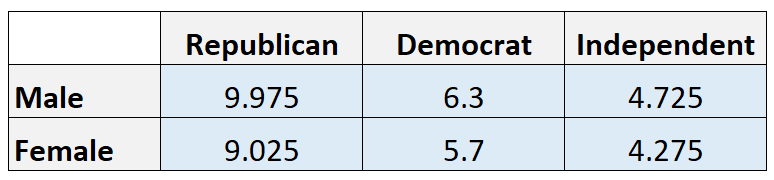
Nota: Calculamos o valor esperado em cada célula multiplicando o total da linha pelo total da coluna e depois dividindo pelo total geral. Por exemplo, o número esperado de homens republicanos é (21*19)/40 = 9,975.

_{Estatística de teste} ^{qui –} _quadrado :

• (|8-9,975| – 0,5) ² /9,975 = 0,218
• (|9-6,3| – 0,5) ² /6,3 = 0,768
• (|4-4,725| – 0,5) ² / 4,725 = 0,011
• (|11-9,025| – 0,5) ² / 9,025 = 0,241
• (|3-5,7| – 0,5) ² /5,7 = 0,849
• (|5-4,275| – 0,5) ² / 4,275 = 0,012

^Então ,

Valor P: De acordo com a calculadora de qui-quadrado para valor P , o valor p que corresponde a uma estatística de teste qui-quadrado com 2 graus de liberdade é 0,3501 .

Como esse valor p não é inferior a 0,05, não conseguiremos rejeitar a hipótese nula. Isto significa que não temos provas suficientes para afirmar que existe uma associação entre género e preferências partidárias.