Covariância

By Dr. benjamim anderson Agosto 5, 2023 Estatisticas 0 Comments

Este artigo explica o que é covariância e como ela é calculada. Você encontrará a fórmula de covariância, bem como um exemplo de cálculo da covariância de um conjunto de dados. Além disso, você pode calcular a covariância de qualquer série de dados com a calculadora online no final.

O que é covariância?

Nas estatísticas, a covariância é um valor que indica o grau de variação conjunta de duas variáveis aleatórias. Em outras palavras, a covariância é utilizada para analisar a dependência entre duas variáveis.

A covariância é igual à soma dos produtos das diferenças entre os dados das duas variáveis e suas respectivas médias dividida pelo número total de dados.

👉 Você pode usar a calculadora abaixo para calcular a covariância de qualquer conjunto de dados.

A interpretação do valor da covariância é muito simples:

Se a covariância for positiva , significa que existe uma dependência entre as duas variáveis. Portanto, quando uma variável aumenta de valor, a outra variável também aumenta e vice-versa.
Se a covariância for negativa , significa que a relação entre as duas variáveis é negativa. Assim, quando uma variável aumenta de valor, a outra variável diminui e vice-versa.
Se a covariância for zero (ou seu valor for próximo de zero), isso implica que não existe relação entre as duas variáveis. Em outras palavras, as duas variáveis aleatórias são independentes.

Como calcular a covariância

Para calcular a covariância de uma série de dados, as seguintes etapas devem ser executadas:

Calcule a média de cada variável separadamente.
Para cada variável, encontre a diferença entre cada um de seus valores e a média da variável.
Multiplique as diferenças calculadas na etapa anterior para cada ponto de dados.
Some todos os resultados obtidos na etapa anterior.
Divida pelo número total de dados. O valor obtido é a covariância da série de dados.

Em resumo, a fórmula para calcular a covariância entre duas variáveis é a seguinte:

$Cov(X,Y)=\cfrac{\displaystyle \sum_{i=1}^n (x_i-\overline{x})(y_i-\overline{y})}{n}$

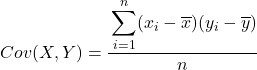
Um método altamente recomendado para extrair a covariância entre duas variáveis é criar uma tabela com todos os pares de dados e adicionar uma coluna para cada uma das etapas explicadas acima. Dessa forma seus cálculos ficarão muito mais organizados e você entenderá melhor o que está fazendo.

Exemplo de cálculo de covariância

Considerando a definição de covariância, segue abaixo um exemplo passo a passo do cálculo desse tipo de medida estatística. O objetivo é que você entenda melhor o conceito de covariância e como analisar a correlação entre duas variáveis.

Calcule a covariância do seguinte conjunto de dados estatísticos:

Primeiro, precisamos calcular a média aritmética de cada variável. Para isso, dividimos a soma dos valores de cada variável pelo número total de dados.

$\overline{x}=\cfrac{58}{10}=5,8$

$\overline{y}=\cfrac{51}{10}=5,1$

➤ Veja: média da fórmula aritmética

Depois de determinar a média de cada variável aleatória, podemos adicionar as seguintes colunas à tabela de dados para obter a covariância:

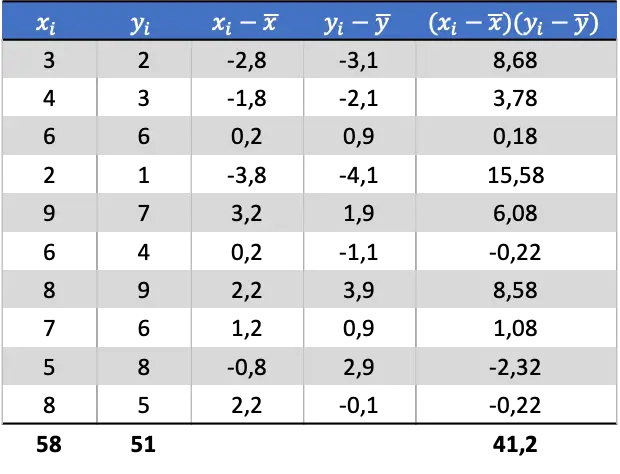
Então para determinar a covariância das duas variáveis você deve dividir a soma da última coluna pelo número de pares de dados:

$\begin{aligned}Cov(X,Y)&=\cfrac{\displaystyle \sum_{i=1}^n (x_i-\overline{x})(y_i-\overline{y})}{n}\\[2ex] Cov(X,Y)&= \cfrac{41,2}{10} \\[2ex]Cov(X,Y)&= 4,12\end{aligned}$

Neste caso o valor da covariância é positivo, o que significa que existe uma dependência direta entre as duas variáveis aleatórias estudadas. Porém, se o valor da covariância fosse negativo, isso significaria que a dependência entre as duas variáveis é inversa. E por fim, se o valor da covariância for zero ou muito próximo de zero, significa que não existe relação linear entre as duas variáveis.

Como você pode ver na resolução deste exemplo, é muito útil usar um programa de computador como o Excel para adicionar as colunas à tabela e realizar os cálculos rapidamente. Caso contrário, calculando as operações manualmente, demora muito mais para encontrar a covariância.

Calculadora de Covariância

Insira um conjunto de dados estatísticos na calculadora a seguir para calcular a covariância entre duas variáveis. Você precisa separar os pares de dados, para que na primeira caixa existam apenas os valores de uma variável e na segunda caixa existam apenas os valores da segunda variável.

Os dados devem ser separados por espaço e inseridos usando o ponto final como separador decimal.

Propriedades de covariância

A covariância tem as seguintes propriedades:

A covariância entre uma variável aleatória e uma constante é zero.

$Cov(X,a)=0$

A covariância de uma variável e ela mesma é equivalente à variância dessa variável.

$Cov(X,X)=Var(X)$

➤ Veja: o que é variância?

A covariância satisfaz a propriedade de simetria, portanto a covariância das variáveis X e Y é igual à covariância das variáveis Y e X. A ordem das variáveis não afeta o resultado da covariância.

$Cov(X,Y)=Cov(Y,X)$

Se as variáveis forem multiplicadas por constantes, você poderá primeiro calcular a covariância e depois multiplicar o resultado pelas constantes.

$Cov(a\cdot X,b\cdot Y)=a\cdot b\cdot Cov(X,Y)$

Adicionar termos às variáveis não afeta o resultado da covariância.

$Cov(a+X,b+Y)=Cov(X+Y)$

A covariância entre duas variáveis aleatórias está relacionada às suas expectativas matemáticas. A covariância entre as variáveis X e Y é igual à expectativa matemática do produto de X e Y menos o produto da expectativa matemática de cada variável.

$Cov(X,Y)=E[X\cdot Y]-E[X]\cdot E[Y]$

Ao operar com variáveis, a seguinte expressão algébrica é preenchida em relação à covariância:

$\begin{aligned}\displaystyle Cov(aX+bY,cW+dV)= \ & \displaystyle acCov(X,W)+adCov(X,V)+\\[2ex]& +bcCov(Y,W)+bdCov(Y,V)\end{aligned}$

About Author

Dr. benjamim anderson

Olá, sou Benjamin, um professor aposentado de estatística que se tornou professor dedicado na Statorials. Com vasta experiência e conhecimento na área de estatística, estou empenhado em compartilhar meu conhecimento para capacitar os alunos por meio de Statorials. Saber mais