O que são curvas de densidade? (explicação e exemplos)

Uma curva de densidade é uma curva em um gráfico que representa a distribuição de valores em um conjunto de dados. Isso é útil por três motivos:

1. Uma curva de densidade nos dá uma boa ideia da “forma” de uma distribuição, incluindo se uma distribuição tem ou não um ou mais “picos” de valores de frequência e se a distribuição está ou não distorcida para a esquerda ou certo. CERTO. .

2. Uma curva de densidade nos permite ver visualmente onde a média e a mediana de uma distribuição se relacionam.

3. Uma curva de densidade nos permite ver visualmente qual porcentagem de observações em um conjunto de dados está entre valores diferentes.

A curva de densidade mais conhecida é a curva em forma de sino que representa a distribuição normal .

Para entender melhor as curvas de densidade, considere o exemplo a seguir.

Exemplo: criação e interpretação de uma curva de densidade

Digamos que temos o seguinte conjunto de dados que mostra a altura de 20 plantas diferentes (em polegadas) em um determinado campo:

4, 5, 5, 6, 6, 6, 6, 7, 7, 7, 7, 7, 8, 8, 8, 9, 9, 9, 2, 2

Se criássemos um histograma simples para exibir as frequências relativas de cada valor, ficaria assim:

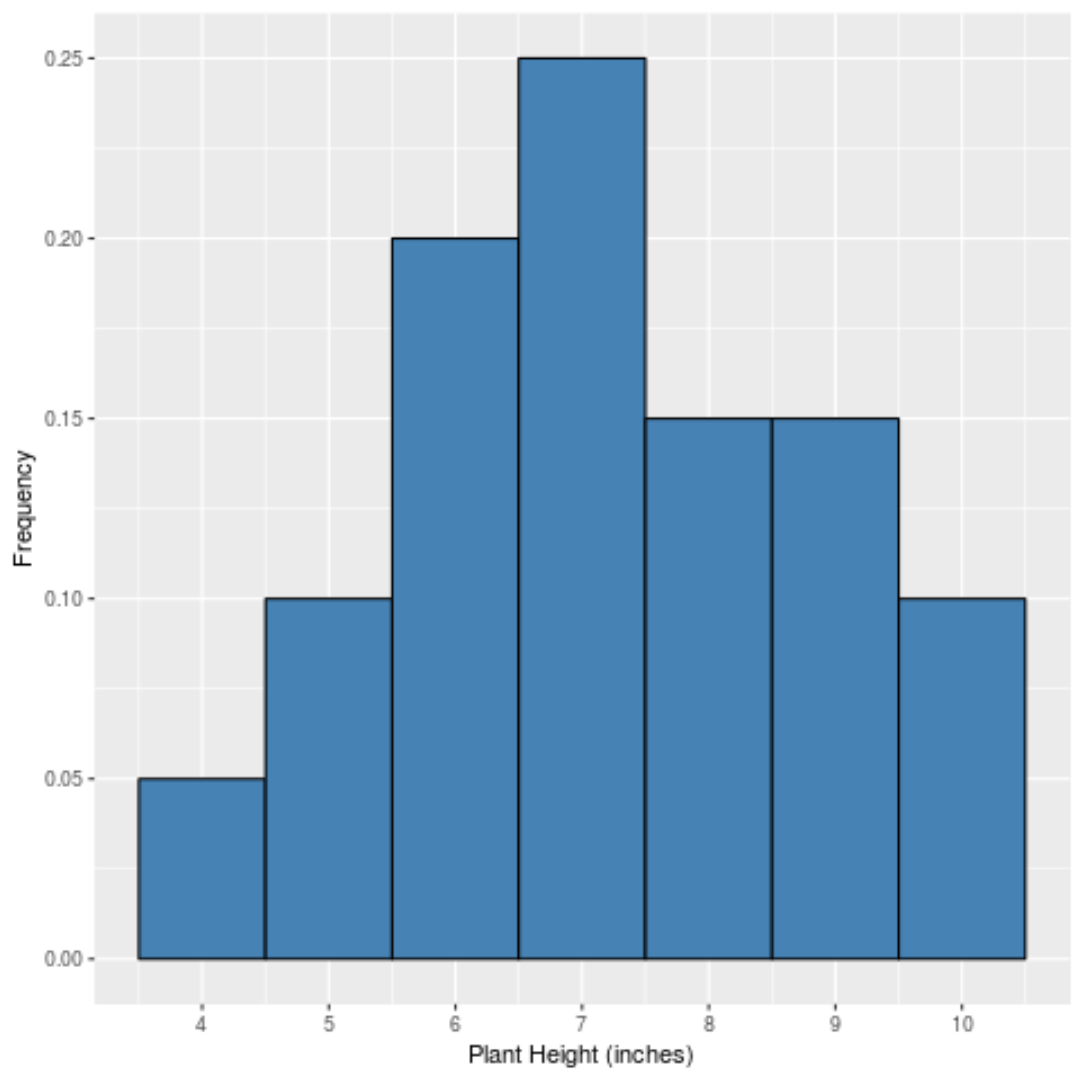
O eixo x mostra o valor dos dados e o eixo y mostra a frequência relativa (por exemplo, o valor “7” aparece 5 vezes em um total de 20 valores no conjunto de dados, portanto tem uma frequência relativa de 25% ou 0,25 .

E se criássemos uma curva de densidade para capturar o “formato” dessa distribuição, ela ficaria assim:

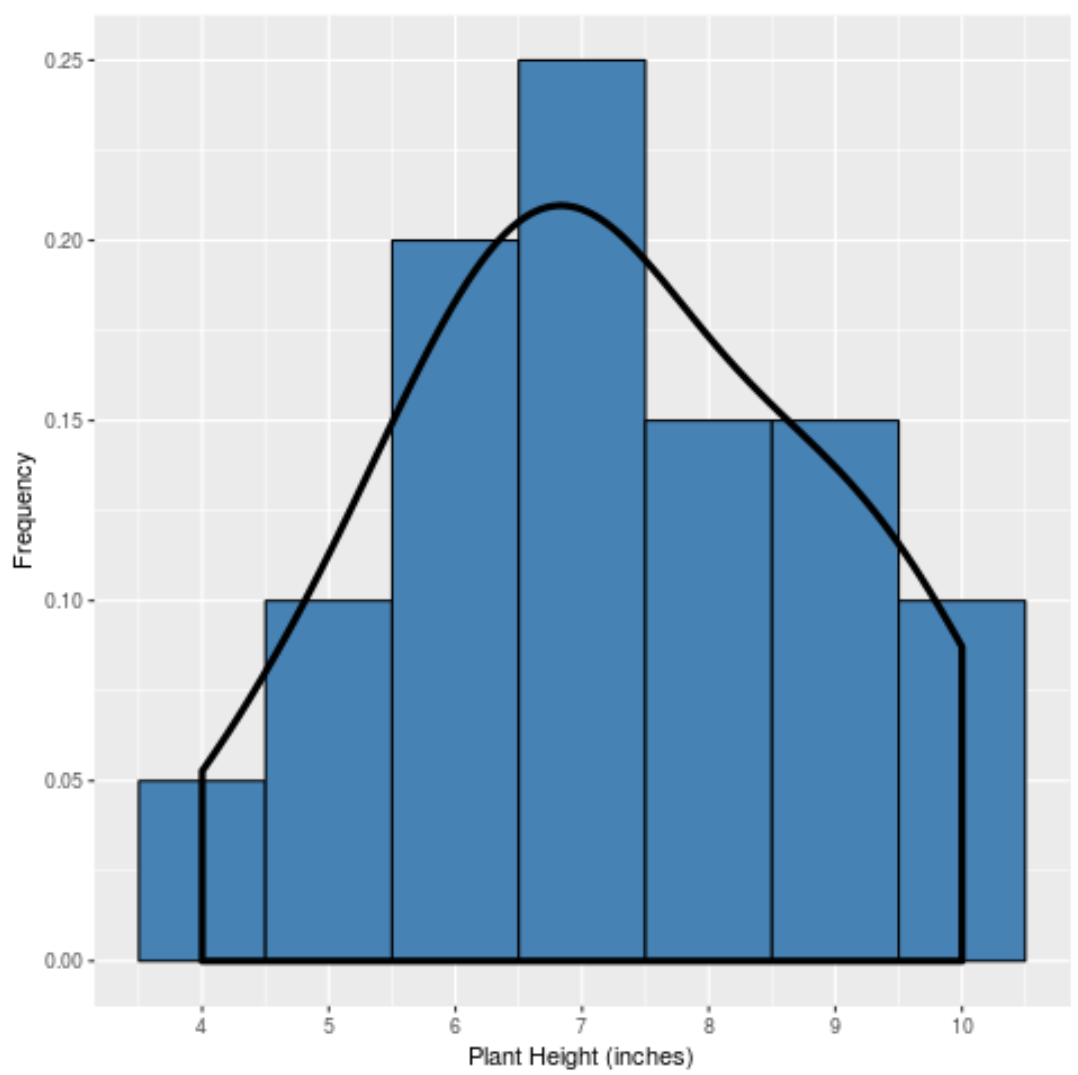
A curva é mais alta perto do centro da distribuição porque é onde se encontra a maioria dos valores. Também é mais baixo perto das extremidades da distribuição porque menos plantas adotam esses valores (por exemplo, altura de 4 polegadas ou 10 polegadas).

Como interpretar curvas de densidade

As curvas de densidade vêm em todos os formatos e tamanhos e nos permitem obter uma rápida compreensão visual da distribuição de valores em um determinado conjunto de dados. Eles são particularmente úteis para nos ajudar a visualizar:

1. Assimetria

Skewness é uma forma de descrever a simetria de uma distribuição. As curvas de densidade nos permitem ver rapidamente se um gráfico está inclinado para a esquerda, para a direita ou não tem inclinação:

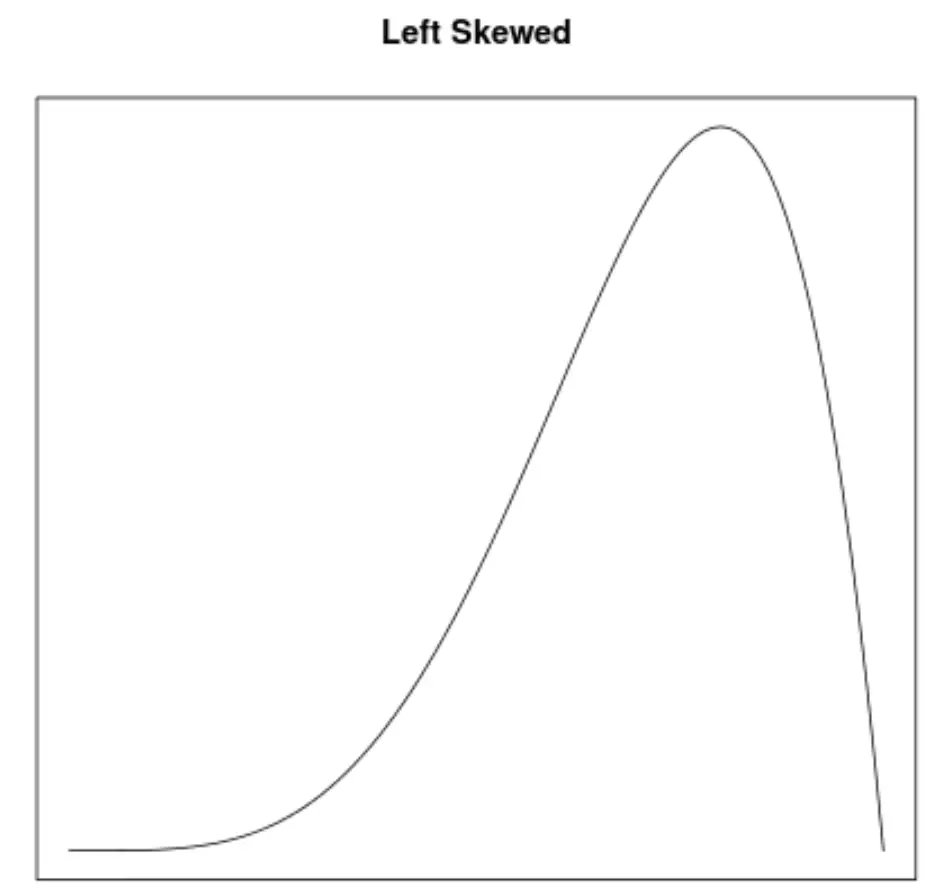
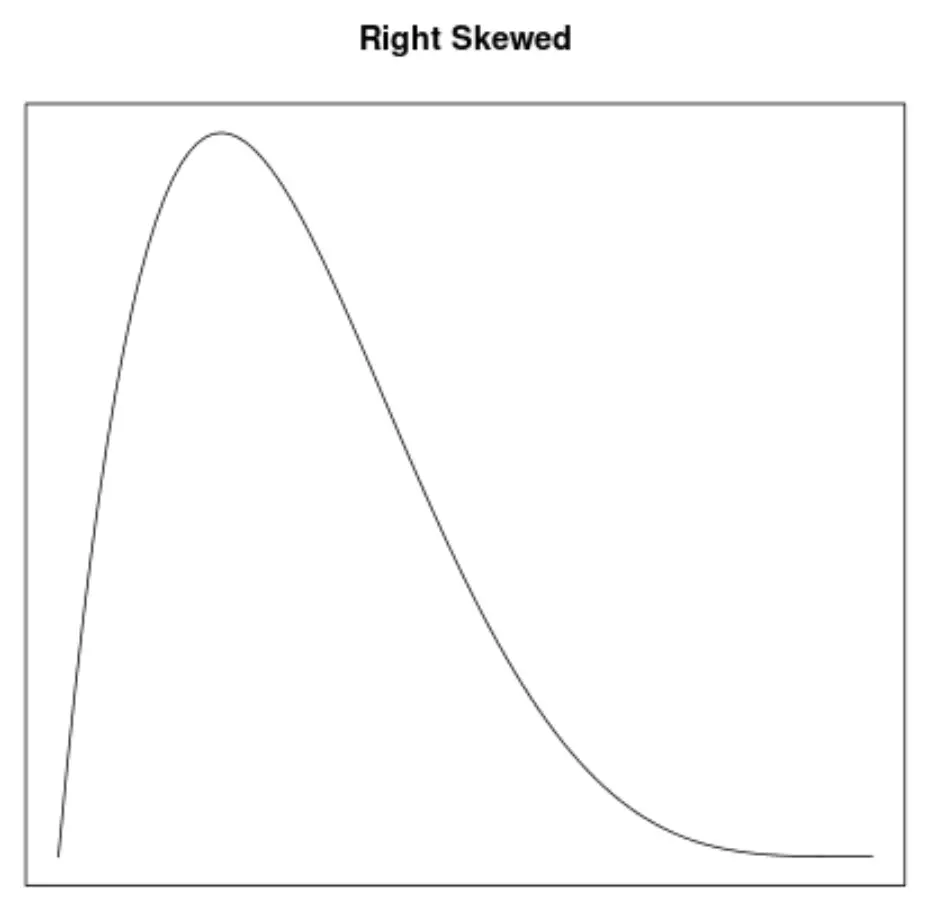
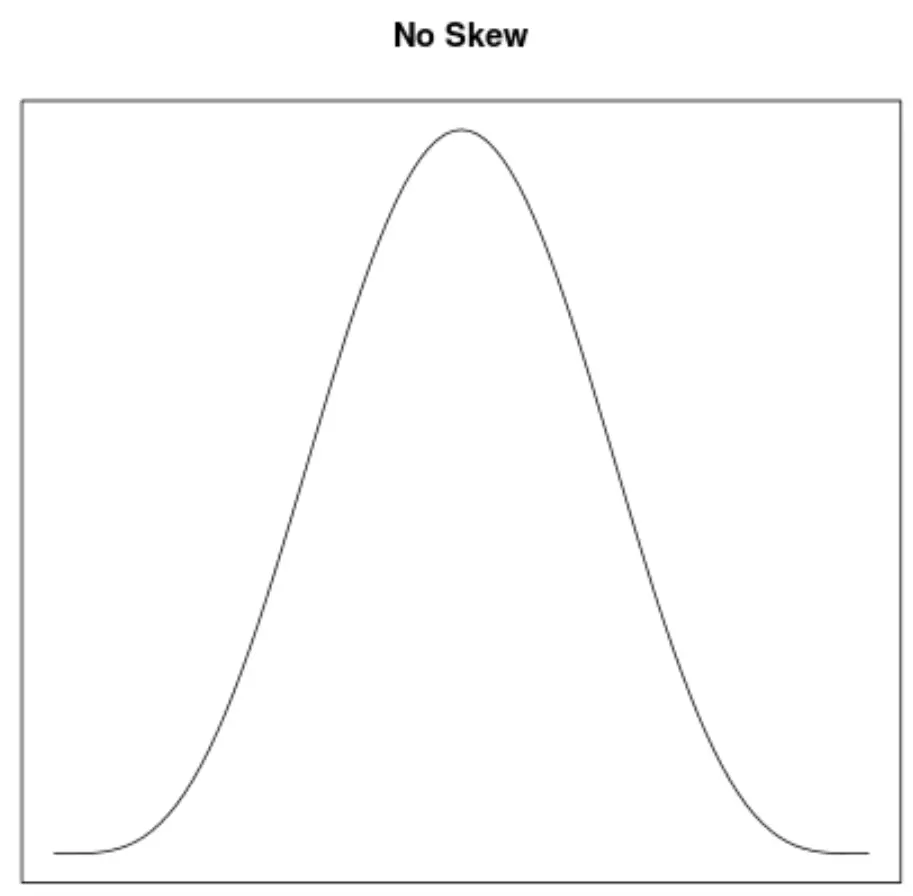
2. A localização da média e mediana

Com base na assimetria de uma curva de densidade, podemos dizer rapidamente se a média ou mediana é maior em uma determinada distribuição. Especialmente:

• Se uma curva de densidade permanecer assimétrica , a média será inferior à mediana.
• Se uma curva de densidade for inclinada para a direita , a média será maior que a mediana.
• Se uma curva de densidade não tiver assimetria , então a média é igual à mediana.

3. Número de picos

As curvas de densidade também nos permitem ver rapidamente quantos “picos” existem em uma determinada distribuição. Em cada um dos exemplos acima, as distribuições tinham apenas um pico, então descreveríamos essas distribuições como unimodais .

No entanto, algumas distribuições podem ter dois picos que chamamos dedistribuições bimodais . E em casos raros também podemos ter distribuições multimodais com dois ou mais picos.

Simplesmente criando uma curva de densidade para um determinado conjunto de dados, podemos ver rapidamente quantos picos existem na distribuição.

Propriedades das curvas de densidade

As curvas de densidade têm as seguintes propriedades:

• A área sob a curva sempre soma 100%.
• A curva nunca ficará abaixo do eixo x.

Tenha esses dois fatos em mente ao criar ou interpretar curvas de densidade para diferentes distribuições.

Recursos adicionais

Introdução aos histogramas de frequência relativa
Como criar uma curva em forma de sino no Excel
Como criar uma curva em forma de sino em Python