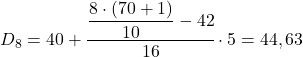Decis

By Dr. benjamim anderson Agosto 5, 2023 Estatisticas 0 Comments

Neste artigo explicamos o que são decis e como são calculados. Você também encontrará vários exemplos resolvidos passo a passo de cálculos de decis e, além disso, poderá calcular os decis de qualquer amostra estatística com uma calculadora online.

O que são decis?

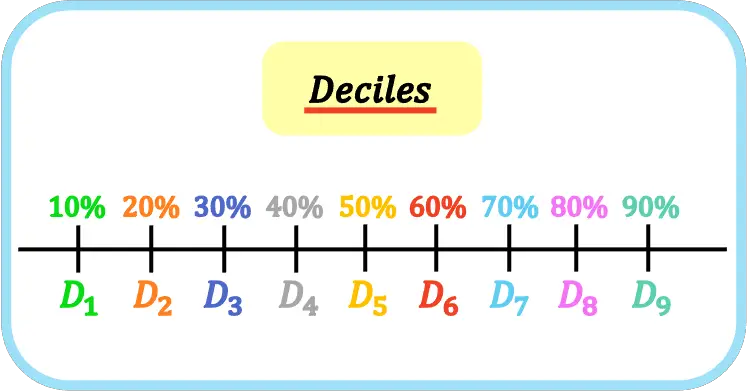
Nas estatísticas, os decis são os nove valores que dividem um conjunto de dados ordenados em dez partes iguais. Para que o primeiro, segundo, terceiro,… decil represente 10%, 20%, 30%,… da amostra ou população.

Por exemplo, o valor do quarto decil é superior a 40% dos dados, mas inferior ao restante dos dados.

Os decis são representados pela letra maiúscula D e pelo índice de decil, ou seja, o primeiro decil é D ₁ , o segundo decil é D ₂ , o terceiro decil é D ₃ , etc.

👉 Você pode usar a calculadora abaixo para calcular decis para qualquer conjunto de dados.

Deve-se notar que os decis são uma medida de posição não central da mesma forma que os quartis, quintis e percentis. Você pode verificar o significado de cada um desses tipos de quantis em nosso site.

Além disso, o quinto decil equivale à mediana e ao segundo quartil, pois dividem todo o conjunto de dados em duas partes iguais.

Como calcular decis

Para calcular a posição decil de uma série de dados estatísticos, multiplique o número decil pela soma do número total de dados mais um e divida o resultado por dez.

A fórmula do decil é, portanto:

$\cfrac{k\cdot (n+1)}{10} \qquad k=1, 2, 3,4,5,6,7,8,9$

Observação: esta fórmula nos informa a posição do decil, não o valor do decil. O decil serão os dados localizados na posição obtida pela fórmula.

Porém, por vezes o resultado desta fórmula nos dará um número decimal, devemos portanto distinguir dois casos dependendo se o resultado é um número decimal ou não:

Se o resultado da fórmula for um número sem parte decimal , o decil é o dado localizado na posição fornecida pela fórmula acima.
Se o resultado da fórmula for um número com parte decimal , o valor do decil é calculado usando a seguinte fórmula:

$D=x_i+d\cdot (x_{i+1}-x_i)$

Onde x _i e x _i+1 são os números das posições entre as quais se localiza o número obtido pela primeira fórmula, ed é a parte decimal do número obtido pela primeira fórmula.

Agora você pode pensar que obter os decis de uma amostra estatística é complexo, mas na prática é bastante simples. Se você ler os dois exemplos a seguir, certamente entenderá muito melhor.

Nota : A comunidade científica não está totalmente de acordo sobre como calcular decis, então você pode encontrar livros de estatística que explicam isso de forma um pouco diferente.

Exemplo de cálculo decil

Como você viu acima, o cálculo dos decis depende se o número que a primeira fórmula nos dá é decimal ou não, por isso preparamos a seguir dois exemplos resolvidos, um para cada caso. De qualquer forma, lembre-se que se você tiver alguma dúvida sobre a composição dos decis, pode perguntar nos comentários.

Exemplo 1

Dados os dados a seguir, do menor para o maior, encontre o primeiro, o terceiro e o oitavo decil da amostra.

Os dados neste exercício já estão ordenados, portanto não há necessidade de alterar a ordem, caso contrário teríamos que ordenar os dados do menor para o maior primeiro.

Conforme explicado acima, a fórmula que permite encontrar as posições dos decis é a seguinte:

$\cfrac{k\cdot (n+1)}{10} \qquad k=1,2,3,4,5,6,7,8,9$

O tamanho da amostra para este exercício é de 29 observações, portanto para calcular a posição do primeiro decil você deve substituir 29 por n e 1 por k :

$\cfrac{1\cdot (29+1)}{10}=3\quad \color{orange}\bm{\longrightarrow}\color{black}\quad D_1=85$

O resultado da fórmula é 3, portanto o primeiro decil estará na terceira posição da lista ordenada, e esse valor corresponde a 85.

Agora aplicamos o mesmo procedimento novamente, mas com o terceiro decil. Usamos a fórmula substituindo k por 3:

$\cfrac{3\cdot (29+1)}{10}=9\quad \color{orange}\bm{\longrightarrow}\color{black}\quad D_3=97$

O terceiro decil será, portanto, o elemento na nona posição, ou seja, 97.

Finalmente, fazemos o mesmo processo, mas colocamos um 8 na fórmula para determinar o oitavo decil:

$\cfrac{8\cdot (29+1)}{10}=24\quad \color{orange}\bm{\longrightarrow}\color{black}\quad D_8=131$

O oitavo decil será o número na posição 24 da lista de dados ordenados, então o oitavo decil é 131.

Exemplo 2

A partir dos dados da tabela a seguir, calcule os decis 4, 7 e 9.

Como no exemplo anterior, para obter as posições dos decis deve-se utilizar a seguinte fórmula:

$\cfrac{k\cdot (n+1)}{10} \qquad k=1,2,3,4,5,6,7,8,9$

Neste caso, o tamanho da amostra é 42, então para encontrar a posição do quarto decil deve-se substituir o parâmetro n por 42 e o k por 4:

$\cfrac{4\cdot (42+1)}{10}=17,2$

Mas desta vez obtivemos um número decimal da fórmula, então precisamos aplicar a seguinte fórmula para calcular o decil exato:

$D=x_i+d\cdot (x_{i+1}-x_i)$

O número obtido na primeira fórmula é 17,2, portanto o quarto decil está entre o décimo sétimo e o décimo oitavo dados, que são 109 e 112 respectivamente. Portanto, x _i é 109, x _{i+ 1} é 112 e d é a parte decimal. do número obtido, ou seja, 0,2.

$D_4=109+0,2\cdot (112-109)=109,6$

Repetimos o mesmo processo para determinar o sétimo decil. Primeiro calculamos a posição do decil:

$\cfrac{7\cdot (42+1)}{10}=30,1$

Da fórmula obtivemos o número 30,1, o que significa que o decil estará entre as posições 30 e 31, cujos valores são 154 e 159. O cálculo do decil exato é portanto:

$D_7=154+0,1\cdot (159-154)=154,5$

Finalmente, aplicamos o mesmo método novamente para obter o nono decil. Determinamos a posição do decil:

$\cfrac{9\cdot (42+1)}{10}=38,7$

O número obtido é decimal e está entre 38 e 39, cujas posições correspondem aos valores 189 e 196. Assim o cálculo do decil 9 é:

$D_9=189+0,7\cdot (196-189)=193,9$

Calculadora de decil

Insira um conjunto de dados estatísticos na calculadora abaixo para calcular decis. Os dados devem ser separados por espaço e inseridos usando o ponto final como separador decimal.

Decis em dados agrupados

Para calcular decis quando os dados são agrupados em intervalos , primeiro precisamos encontrar o intervalo ou compartimento em que o decil se enquadra usando a seguinte fórmula:

$\cfrac{k\cdot (n+1)}{10} \qquad k=1, 2, 3,3,4,5,6,7,8,9$

O decil estará portanto no intervalo cuja frequência absoluta é imediatamente maior que o número obtido na expressão anterior.

E uma vez que já sabemos a que intervalo pertence o decil, devemos aplicar a seguinte fórmula para encontrar o valor exato do decil:

$D_k=L_i+\cfrac{\displaystyle\frac{k\cdot (n+1)}{10}-F_{i-1}}{f_i}\cdot I_i \qquad k=1,2,3,4,5,6,7,8,9$

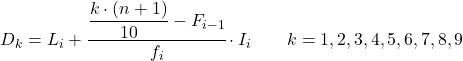
Ouro:

L _i é o limite inferior do intervalo em que o decil está localizado.
n é o número total de dados estatísticos.
F _i-1 é a frequência absoluta acumulada do intervalo anterior.
f _i é a frequência absoluta do intervalo em que o decil está localizado.
I _i é a largura do intervalo decil.

Para que você possa ver como isso é feito, abaixo você tem um exercício completo no qual são calculados os decis 3, 5 e 8 dos seguintes dados agrupados por intervalos.

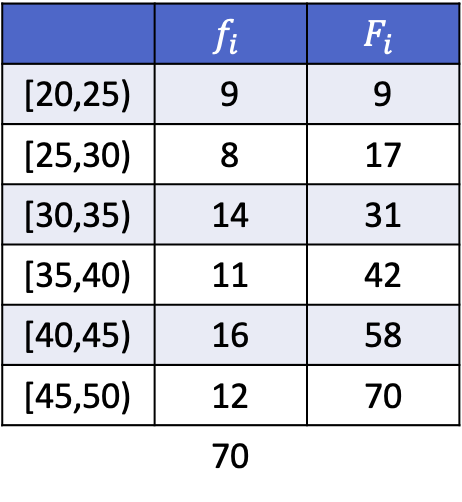
Como os dados estão agrupados, o cálculo de cada decil consiste em duas etapas: primeiro, encontre o intervalo em que o decil cai e, em seguida, calcule o valor exato do decil. Portanto, encontramos o intervalo do terceiro decil:

$\cfrac{k\cdot (n+1)}{10}$

$\cfrac{3\cdot (70+1)}{10} =21,3 \quad \color{orange}\bm{\longrightarrow}\color{black}\quad [30,35)$

O intervalo decil será aquele cuja frequência acumulada absoluta é imediatamente maior que 21,3, e neste caso é o intervalo [30,35) cuja frequência acumulada absoluta é 31. Agora que conhecemos o intervalo decil, aplicamos a seguinte fórmula para encontrar o valor exato do decil:

$D_k=L_i+\cfrac{\displaystyle\frac{k\cdot (n+1)}{10}-F_{i-1}}{f_i}\cdot I_i$

$D_3=30+ \cfrac{\displaystyle\frac{3\cdot (70+1)}{10}-17}{14}\cdot 5=31,54$

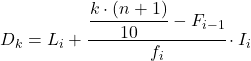
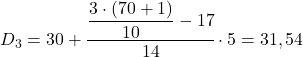
Devemos agora reaplicar o método para obter o quinto decil. Primeiro determinamos o intervalo em que se encontra:

$\cfrac{5\cdot (70+1)}{10} =35,5 \quad \color{orange}\bm{\longrightarrow}\color{black}\quad [35,40)$

O resultado 35 significa que está no intervalo [35,40), mas não porque haja um 35 na expressão intervalar, mas porque sua frequência absoluta acumulada (42) é a mais imediatamente alta. E uma vez identificado o intervalo, aplicamos a segunda fórmula do processo:

$D_5=35+ \cfrac{\displaystyle\frac{5\cdot (70+1)}{10}-31}{11}\cdot 5=37,05$

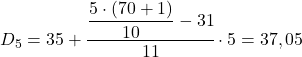
Finalmente, encontramos o oitavo decil. Para fazer isso, primeiro calculamos seu intervalo:

$\cfrac{8\cdot (70+1)}{10} =56,8 \quad \color{orange}\bm{\longrightarrow}\color{black}\quad [40,45)$

A frequência absoluta cumulativa imediatamente acima de 56,8 é 58, então a faixa do oitavo decil é [40,45). Portanto, é suficiente determinar o valor exato do decil:

$D_8=40+ \cfrac{\displaystyle\frac{8\cdot (70+1)}{10}-42}{16}\cdot 5=44,63$

About Author

Dr. benjamim anderson

Olá, sou Benjamin, um professor aposentado de estatística que se tornou professor dedicado na Statorials. Com vasta experiência e conhecimento na área de estatística, estou empenhado em compartilhar meu conhecimento para capacitar os alunos por meio de Statorials. Saber mais