Desvio padrão da amostra (ou desvio padrão da amostra)

Este artigo explica o que é o desvio padrão da amostra nas estatísticas. Da mesma forma, você aprenderá como calcular o desvio padrão amostral, um exercício resolvido e qual a diferença entre o desvio padrão amostral e o desvio padrão populacional. Finalmente, você pode calcular qualquer desvio padrão amostral com uma calculadora online.

Qual é o desvio padrão da amostra?

O desvio padrão amostral (ou desvio padrão amostral ) é uma medida de dispersão que indica a variabilidade de uma amostra. Mais precisamente, o desvio padrão da amostra é igual à raiz quadrada da soma dos quadrados dos desvios dividida pelo tamanho da amostra menos um.

O símbolo do desvio padrão amostral é a letra minúscula s .

O desvio padrão da amostra é às vezes chamado de desvio quase padrão (ou desvio quase padrão) para distingui-lo do desvio padrão da população. A seguir veremos como o desvio padrão da amostra difere do desvio padrão da população.

Exemplo de fórmula de desvio padrão

O desvio padrão da amostra é igual à raiz quadrada da soma dos quadrados dos desvios dos dados amostrais dividida pelo tamanho da amostra menos um. Portanto, a fórmula para cálculo do desvio padrão amostral é:

Ouro:

• 

  é o desvio padrão da amostra (ou desvio padrão da amostra).

• 

  é o valor dos dados

  

  .

• 

  é o tamanho da amostra

• 

  é a média amostral.

👉 Você pode usar a calculadora abaixo para calcular o desvio padrão de qualquer amostra de dados.

Exemplo de cálculo do desvio padrão amostral

Agora que sabemos a definição de desvio padrão amostral (ou desvio padrão amostral) e qual é sua fórmula, resolveremos um exemplo simples para finalizar o entendimento de como ele é calculado.

• Uma empresa de calçados está conduzindo uma pesquisa de mercado para decidir se lançará um novo modelo de calçado. Como existem muitos modelos diferentes e você deseja apenas fazer uma rápida análise preliminar, você decide apenas olhar o preço de uma amostra das cinco principais marcas de calçados concorrentes (os preços são mostrados abaixo). Qual é o desvio padrão deste conjunto de dados?

98€ 70€ 125€ 89€ 75€

Para calcular o desvio padrão amostral, primeiro precisamos calcular a média amostral :

Uma vez calculada a média amostral, aplicamos a fórmula do desvio padrão amostral:

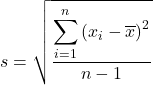
Substituímos os dados da amostra na fórmula:

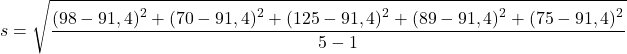
Então, resta resolver as operações para calcular o desvio padrão amostral:

A diferença amostral da amostra analisada é, portanto, de 21,82€.

Desvio padrão amostral e desvio padrão populacional

A seguir, veremos quais são as diferenças entre o desvio padrão da amostra e o desvio padrão da população, porque esses são dois conceitos estatísticos relacionados que precisamos ter clareza.

Na estatística, o desvio padrão da população é o desvio padrão que se obtém ao calcular com todos os elementos da população, embora o desvio padrão seja o desvio padrão que se obtém realizando o cálculo com apenas um exemplo de dados da população .

Matematicamente, a diferença entre o desvio padrão amostral e o desvio padrão populacional é o denominador da fórmula utilizada para o seu cálculo. Para calcular o desvio padrão amostral, ele deve ser dividido por n-1, enquanto o desvio padrão populacional é calculado dividindo-se por n.

Além disso, para diferenciar o desvio padrão amostral do desvio padrão populacional, eles são representados por símbolos diferentes. O símbolo do desvio padrão da amostra é a letra s, enquanto o símbolo do desvio padrão da população é a letra grega σ.

Em geral, nem todos os elementos de uma população são conhecidos, pelo que o estudo estatístico é realizado sobre uma amostra da população. Assim, o desvio padrão da amostra é usado para fazer uma estimativa pontual do valor do desvio padrão de toda a população.

Exemplo de calculadora de desvio padrão

Insira os dados de uma amostra na calculadora on-line a seguir para calcular seu desvio padrão amostral (ou desvio padrão amostral). Os dados devem ser separados por espaço e inseridos usando o ponto final como separador decimal.