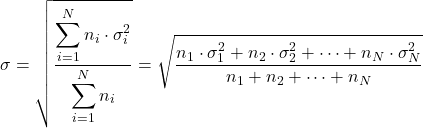Desvio padrão (ou desvio padrão)

By Dr. benjamim anderson Agosto 5, 2023 Estatisticas 0 Comments

Este artigo explica o que é o desvio padrão, também chamado de desvio padrão. Você aprenderá como calcular o desvio padrão, um exemplo prático passo a passo e uma calculadora online para encontrar o desvio padrão de qualquer amostra de dados.

Qual é o desvio padrão (ou desvio padrão)?

O desvio padrão , também chamado de desvio padrão , é uma medida de dispersão estatística. Em outras palavras, o desvio padrão é um valor que indica a dispersão de um conjunto de dados estatísticos.

Portanto, o desvio padrão (ou desvio padrão) é utilizado para quantificar a dispersão de uma população ou amostra estatística. Quanto maior o desvio padrão de uma série de dados, mais dispersos são os dados. E a interpretação também pode ser feita no sentido contrário, se o desvio padrão for baixo isso significa que em geral os dados estão muito próximos da sua média.

Ao calcular o desvio padrão ou típico sobre uma população, o símbolo do desvio padrão é a letra grega sigma (σ). Mas quando se trata de desvio padrão amostral, a letra s é usada para representar a medida estatística.

Em alguns livros de estatística e probabilidade, o desvio padrão também é chamado de desvio padrão.

Fórmula de desvio padrão (ou desvio padrão)

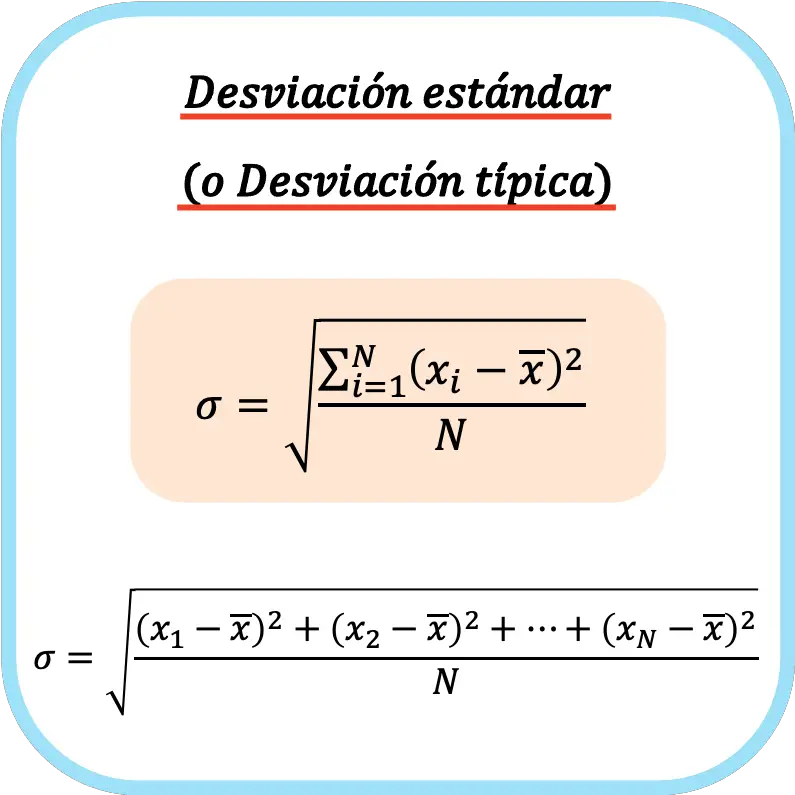
O desvio padrão (ou desvio padrão) é igual à raiz quadrada da soma dos quadrados dos desvios da série de dados dividida pelo número total de observações.

A fórmula para calcular o desvio padrão (ou desvio padrão) é portanto:

👉 Você pode usar a calculadora abaixo para calcular o desvio padrão de qualquer conjunto de dados.

Concluindo, para encontrar o desvio padrão de um conjunto de dados, você precisa calcular todos os desvios (definidos como a diferença entre um ponto de dados e a média aritmética), aumentar os desvios para dois, somar todos e depois dividir pelo total. número de dados e, finalmente, tirar a raiz quadrada.

Exemplo de desvio padrão (ou desvio padrão)

Considerando a definição de desvio padrão (ou desvio típico), segue abaixo um exemplo passo a passo para que você possa ver como é calculado o desvio padrão de uma série de dados.

Calcule o desvio padrão dos seguintes valores: 3, 6, 2, 9, 4.

A primeira coisa que precisamos fazer é determinar a média amostral. Para isso, somamos todos os dados e dividimos pelo número total de observações, que é cinco:

$\overline{x}=\cfrac{3+6+2+9+4}{5}=4,8$

Agora usamos a fórmula do desvio padrão:

$\displaystyle\sigma=\sqrt{\frac{\displaystyle\sum_{i=1}^N(x_i-\overline{x})^2}{N}}$

Substituímos os dados na fórmula:

$\displaystyle\sigma =\sqrt{\frac{(3-4,8)^2+(6-4,8)^2+(2-4,8)^2+(9-4,8)^2+(4-4,8)^2}{5}}$

E finalmente calculamos o desvio padrão:

$\begin{aligned}\displaystyle\sigma & = \sqrt{\frac{(-1,8)^2+1,2^2+(-2,8)^2+4,2^2+(-0,8)^2}{5}}\\[2ex]&=\sqrt{\frac{3,24+1,44+7,84+17,64+0,64}{5}}\\[2ex]&= \sqrt{\frac{30,8}{5}}=\sqrt{6,16}=2,48 \end{aligned}$

Calculadora de desvio padrão (ou desvio padrão)

Insira um conjunto de dados estatísticos na calculadora online a seguir para calcular seu desvio padrão (ou desvio padrão). Os dados devem ser separados por espaço e inseridos usando o ponto final como separador decimal.

Desvio padrão (ou típico) para dados agrupados

Para calcular o desvio padrão (ou desvio padrão) dos dados agrupados em intervalos , devem ser seguidos os seguintes passos:

Encontre a média dos dados agrupados.
Calcule desvios de dados agrupados.
Quadre cada lacuna.
Multiplique cada resultado anterior pela frequência de seu intervalo.
Some a soma de todos os valores obtidos na etapa anterior.
Divida pelo número total de observações.
Tire a raiz quadrada do valor anterior. O número resultante é o desvio padrão dos dados agrupados.

Concluindo, a fórmula para cálculo do desvio padrão dos dados agrupados em intervalos é:

$\displaystyle\sigma=\sqrt{\frac{\displaystyle\sum_{i=1}^N\left(x_i-\overline{x}\right)^2\cdot f_i }{N}}$

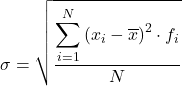
Embora a fórmula acima seja normalmente usada, a seguinte expressão algébrica também pode ser usada, pois o mesmo resultado é obtido:

$\displaystyle\sigma=\sqrt{\frac{\displaystyle\sum_{i=1}^n x_i^2\cdot f_i }{N}-\overline{x}^2}$

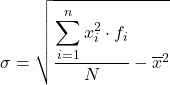
Para que você possa ver como isso é feito, segue abaixo um passo a passo do exercício sobre o desvio padrão de dados agrupados em intervalos. Mais precisamente, será calculado o desvio padrão dos seguintes dados estatísticos:

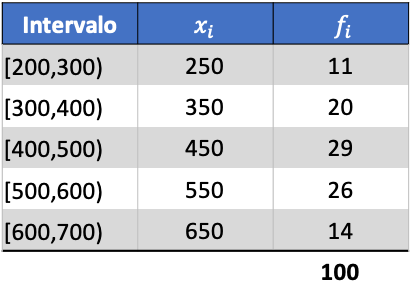
exemplo de dados agrupados em intervalos

Primeiro, multiplicamos a pontuação da turma de cada intervalo pela sua frequência para calcular a média aritmética:

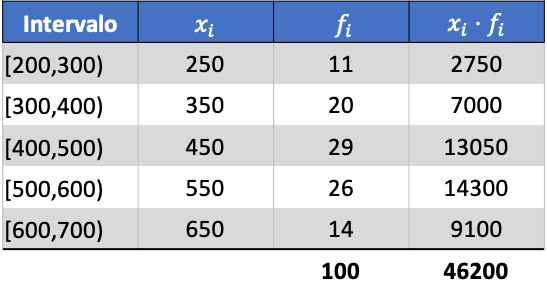
Portanto, a média dos dados agrupados será:

$\overline{x}=\cfrac{\displaystyle\sum_{i=1}^n x_i\cdot f_i}{N}=\cfrac{46200}{100}=462$

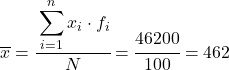
Agora que sabemos o valor da média, precisamos adicionar as três colunas a seguir à tabela de dados:

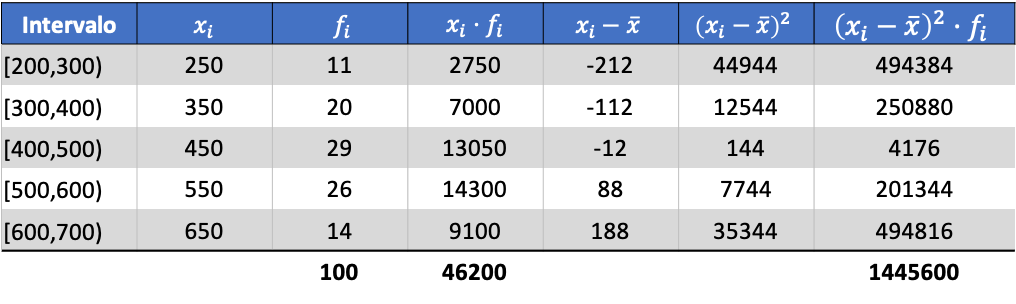
exercício resolvido de desvio padrão ou desvio padrão para dados agrupados

Então o desvio padrão dos dados agrupados será o resultado da raiz quadrada do total da última coluna dividido pelo número total de observações:

$\displaystyle\sigma=\sqrt{\frac{\displaystyle\sum_{i=1}^N\left(x_i-\overline{x}\right)^2\cdot f_i }{N}}=\sqrt{\frac{1445600}{100}}=120,23$

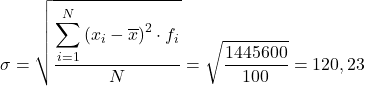
Desvio e variância padrão (ou típico)

A relação entre o desvio padrão (ou desvio típico) e a variância é que o desvio padrão é a raiz quadrada da variância.

Portanto, se conhecermos o valor da variância de um conjunto de dados, podemos calcular facilmente o desvio padrão extraindo a raiz quadrada. Ou, inversamente, se conhecermos o desvio padrão, podemos determinar a variância elevando o valor ao quadrado.

$Var(X)=\sigma^2$

Na verdade, a variância pode ser representada simplesmente usando o símbolo do desvio padrão ao quadrado. Portanto, o símbolo da variância populacional é sigma ao quadrado (σ ² ) e o símbolo da variância amostral é s ao quadrado (s ² ).

Adicionalmente, os conceitos de desvio padrão e variância têm interpretação semelhante, pois ambos mostram a dispersão de uma série de dados estatísticos.

Propriedades do desvio padrão (ou desvio padrão)

O desvio padrão tem as seguintes propriedades:

O desvio padrão de uma amostra de dados não pode ser negativo.

$\sigma \ge 0$

O desvio padrão será zero se todos os dados forem iguais.

$\sigma =0$

Se um termo constante for adicionado a todos os dados, o valor do desvio padrão não muda.

$\sigma (X+k)=\sigma (X)$

Se todos os dados forem multiplicados por um número, o desvio padrão será multiplicado pelo valor absoluto desse número.

$\sigma (k\cdot X)=|k|\cdot \sigma (X)$

O desvio padrão da soma de duas variáveis aleatórias é igual à raiz quadrada da soma das variâncias das variáveis mais o dobro da covariância entre as duas variáveis.

$\sigma(X+Y)=\sqrt{Var(X)+Var(Y)+2\cdot Cov(X,Y)}$

Se conhecermos os desvios padrão das diferentes distribuições (σ _i ) e o seu número de dados (ni ₎ , podemos calcular o desvio padrão total aplicando a seguinte fórmula:

$\displaystyle\sigma=\sqrt{\frac{\displaystyle \sum_{i=1}^N n_i\cdot \sigma_i^2}{\displaystyle \sum_{i=1}^N n_i}}=\sqrt{\frac{\displaystyle n_1\cdot \sigma_1^2+n_2\cdot \sigma_2^2+\dots +n_N\cdot \sigma_N^2}{\displaystyle n_1+n_2+\dots+n_N}}$

About Author

Dr. benjamim anderson

Olá, sou Benjamin, um professor aposentado de estatística que se tornou professor dedicado na Statorials. Com vasta experiência e conhecimento na área de estatística, estou empenhado em compartilhar meu conhecimento para capacitar os alunos por meio de Statorials. Saber mais