Desvio padrão e erro padrão: qual a diferença?

Dois termos que os alunos costumam confundir em estatística são desvio padrão e erro padrão .

O desvio padrão mede a distribuição de valores em um conjunto de dados.

O erro padrão é o desvio padrão da média de amostras repetidas de uma população.

Vejamos um exemplo para ilustrar claramente essa ideia.

Exemplo: desvio padrão versus erro padrão

Suponha que medimos o peso de 10 tartarugas diferentes.

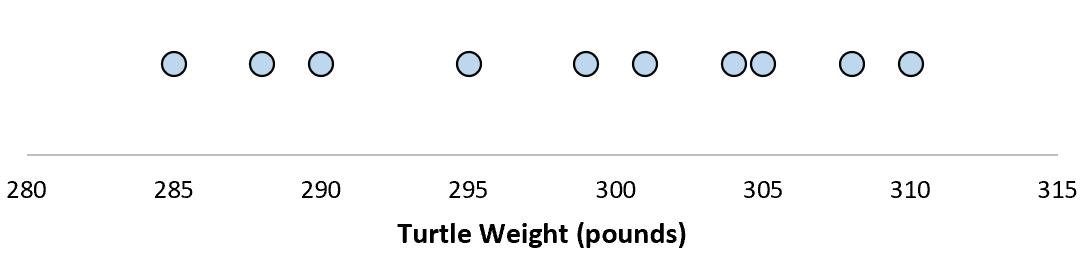
Para esta amostra de 10 tartarugas, podemos calcular a média amostral e o desvio padrão amostral:

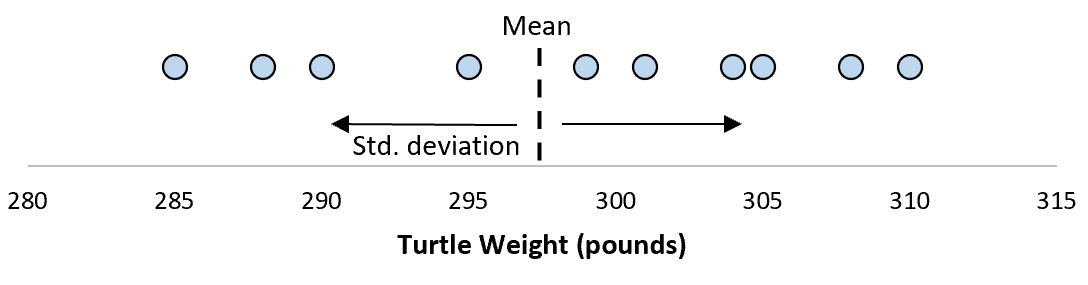
Suponha que o desvio padrão seja 8,68. Isso nos dá uma ideia da distribuição de peso dessas tartarugas.

Mas suponhamos que recolhamos outra amostra aleatória simples de 10 tartarugas e também façamos as suas medições.

É mais do que provável que esta amostra de 10 tartarugas tenha uma média e um desvio padrão ligeiramente diferentes, embora venham da mesma população:

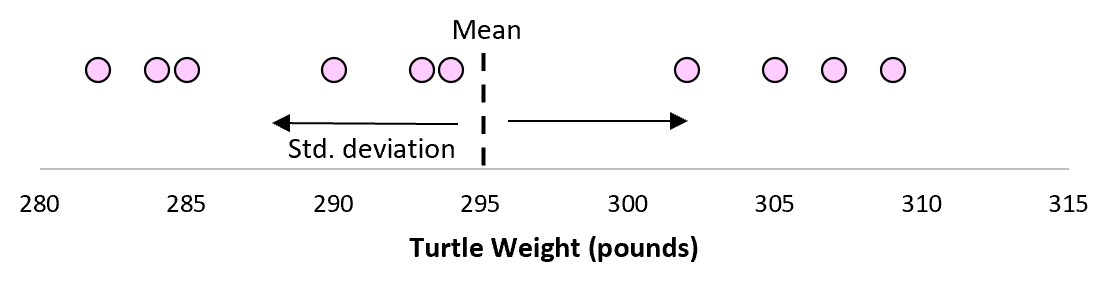
Agora, se imaginarmos que pegamos amostras repetidas da mesma população e registramos a média amostral e o desvio padrão amostral para cada amostra:

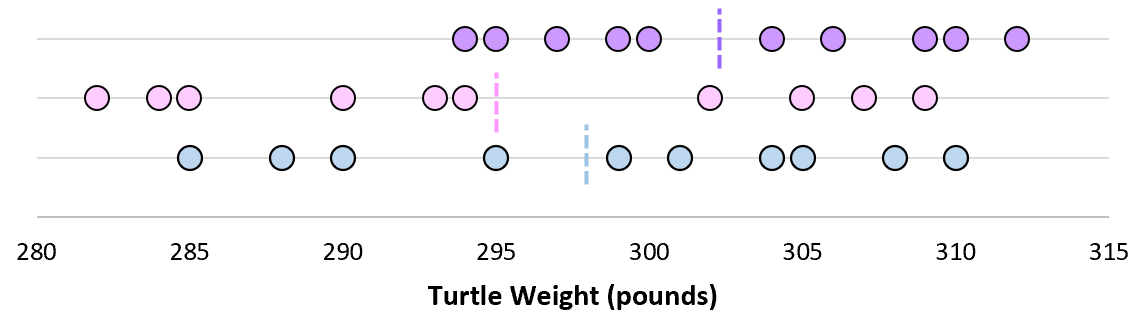
Agora imagine que plotamos cada uma das médias amostrais na mesma linha:

O desvio padrão dessas médias é chamado de erro padrão.

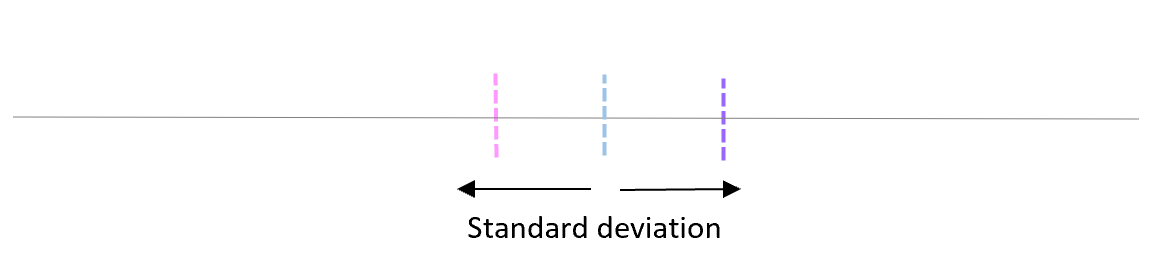
A fórmula para realmente calcular o erro padrão é:

Erro padrão = s/ √ n

Ouro:

• s: desvio padrão da amostra
• n: tamanho da amostra

Qual é o sentido de usar o erro padrão?

Quando calculamos a média de uma determinada amostra, não estamos realmente procurando saber a média dessa amostra específica, mas sim a média da população maior da qual provém a amostra.

No entanto, utilizamos amostras porque é muito mais fácil recolher dados para elas do que para uma população inteira.

E, claro, a média amostral varia de amostra para amostra, por isso utilizamos o erro padrão da média como forma de medir a precisão da nossa estimativa da média.

Você notará na fórmula de cálculo do erro padrão que à medida que o tamanho da amostra (n) aumenta, o erro padrão diminui:

Erro padrão = s/ √ n

Isto deve fazer sentido, porque amostras maiores reduzem a variabilidade e aumentam a probabilidade de a nossa média amostral estar mais próxima da verdadeira média populacional.

Quando usar o desvio padrão versus erro padrão

Se quisermos simplesmente medir a distribuição de valores em um conjunto de dados, podemos usar o desvio padrão .

Contudo, se quisermos quantificar a incerteza em torno de uma estimativa da média, podemos utilizar o erro padrão da média .

Dependendo do seu cenário específico e do que você está tentando realizar, você pode optar por usar o desvio padrão ou o erro padrão.