Como calcular dfbetas em r

Nas estatísticas, muitas vezes queremos saber qual a influência que diferentes observações têm nos modelos de regressão.

Uma forma de calcular a influência das observações é usar uma métrica conhecida como DFBETAS , que nos informa o efeito padronizado em cada coeficiente da remoção de cada observação individual.

Essa métrica nos dá uma ideia da influência de cada observação em cada estimativa de coeficiente em um determinado modelo de regressão.

Este tutorial mostra um exemplo passo a passo de como calcular e visualizar DFBETAS para cada observação em um modelo em R.

Passo 1: Crie um modelo de regressão

Primeiro, criaremos um modelo de regressão linear múltipla usando o conjunto de dados mtcars integrado ao R:

 #fit a regression model
model <- lm(mpg~disp+hp, data=mtcars)

#view model summary
summary(model)

Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept) 30.735904 1.331566 23.083 < 2nd-16 ***
available -0.030346 0.007405 -4.098 0.000306 ***
hp -0.024840 0.013385 -1.856 0.073679 .  
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 3.127 on 29 degrees of freedom
Multiple R-squared: 0.7482, Adjusted R-squared: 0.7309 
F-statistic: 43.09 on 2 and 29 DF, p-value: 2.062e-09

Passo 2: Calcular DFBETAS para cada observação

A seguir, usaremos a função integrada dfbetas() para calcular os valores DFBETAS para cada observação no modelo:

 #calculate DFBETAS for each observation in the model
dfbetas <- as . data . frame (dfbetas(model))

#display DFBETAS for each observation
dfbetas

                      (Intercept) disp hp
Mazda RX4 -0.1174171253 0.030760632 1.748143e-02
Mazda RX4 Wag -0.1174171253 0.030760632 1.748143e-02
Datsun 710 -0.1694989349 0.086630144 -3.332781e-05
Hornet 4 Drive 0.0577309674 0.078971334 -8.705488e-02
Hornet Sportabout -0.0204333878 0.237526523 -1.366155e-01
Valiant -0.1711908285 -0.139135639 1.829038e-01
Duster 360 -0.0312338677 -0.005356209 3.581378e-02
Merc 240D -0.0312259577 -0.010409922 2.433256e-02
Merc 230 -0.0865872595 0.016428917 2.287867e-02
Merc 280 -0.1560683502 0.078667906 -1.911180e-02
Merc 280C -0.2254489597 0.113639937 -2.760800e-02
Merc 450SE 0.0022844093 0.002966155 -2.855985e-02
Merc 450SL 0.0009062022 0.001176644 -1.132941e-02
Merc 450SLC 0.0041566755 0.005397169 -5.196706e-02
Cadillac Fleetwood 0.0388832216 -0.134511133 7.277283e-02
Lincoln Continental 0.0483781688 -0.121146607 5.326220e-02
Chrysler Imperial -0.1645266331 0.236634429 -3.917771e-02
Fiat 128 0.5720358325 -0.181104179 -1.265475e-01
Honda Civic 0.3490872162 -0.053660545 -1.326422e-01
Toyota Corolla 0.7367058819 -0.268512348 -1.342384e-01
Toyota Corona -0.2181110386 0.101336902 5.945352e-03
Dodge Challenger -0.0270169005 -0.123610713 9.441241e-02
AMC Javelin -0.0406785103 -0.141711468 1.074514e-01
Camaro Z28 0.0390139262 0.012846225 -5.031588e-02
Pontiac Firebird -0.0549059340 0.574544346 -3.689584e-01
Fiat X1-9 0.0565157245 -0.017751582 -1.262221e-02
Porsche 914-2 0.0839169111 -0.028670987 -1.240452e-02
Lotus Europa 0.3444562478 -0.402678927 2.135224e-01
Ford Pantera L -0.1598854695 -0.094184733 2.320845e-01
Ferrari Dino -0.0343997122 0.248642444 -2.344154e-01
Maserati Bora -0.3436265545 -0.511285637 7.319066e-01
Volvo 142E -0.1784974091 0.132692956 -4.433915e-02

Para cada observação, podemos ver a diferença na estimativa do coeficiente para a origem, a variável disp e a variável hp que ocorre quando removemos aquela observação específica.

Geralmente, consideramos que uma observação tem forte influência na estimativa de um determinado coeficiente se tiver um valor DBETAS superior a um limite de 2/√ n onde n é o número de observações.

Neste exemplo, o limite seria 0,3535534 :

 #find number of observations
n <- nrow (mtcars)

#calculate DFBETAS threshold value
thresh <- 2/ sqrt (n)

thresh

[1] 0.3535534

Passo 3: Visualize o DFBETAS

Finalmente, podemos criar gráficos para visualizar o valor DFBETAS para cada observação e para cada preditor no modelo:

 #specify 2 rows and 1 column in plotting region
by(mfrow=c(2,1))

#plot DFBETAS for disp with threshold lines
plot(dfbetas$disp, type=' h ')
abline(h = thresh, lty = 2)
abline(h = -thresh, lty = 2)

#plot DFBETAS for hp with threshold lines 
plot(dfbetas$hp, type=' h ')
abline(h = thresh, lty = 2)
abline(h = -thresh, lty = 2)

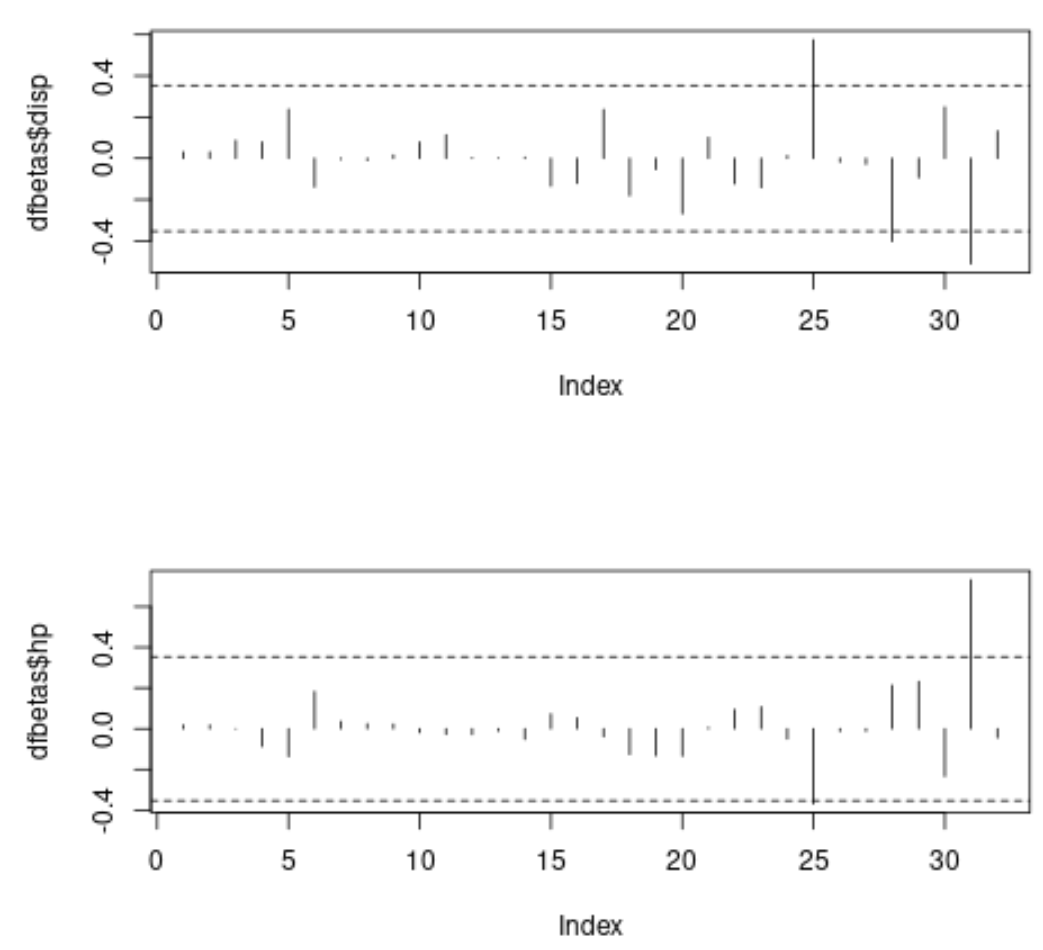
Em cada gráfico, o eixo x exibe o índice de cada observação no conjunto de dados e o valor y exibe os DFBETAS correspondentes para cada observação e cada preditor.

No primeiro gráfico podemos ver que três observações excedem o valor limite absoluto de 0,3535534 e no segundo gráfico podemos ver que duas observações excedem o valor limite absoluto.

Podemos optar por estudar estas observações mais de perto para determinar se elas têm uma influência indevida na estimativa dos coeficientes do modelo.

Recursos adicionais

Como realizar regressão linear simples em R
Como realizar regressão linear múltipla em R
Como calcular estatísticas de alavancagem em R
Como calcular DFFITS em R